Stochastic Gradient Methods with Compressed Communication for Decentralized Saddle Point Problems

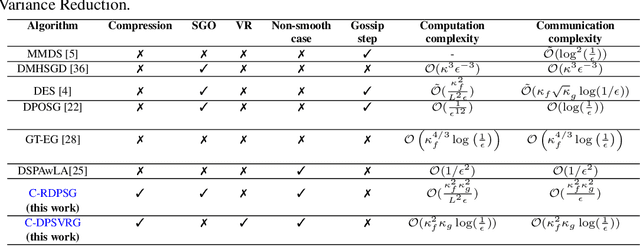
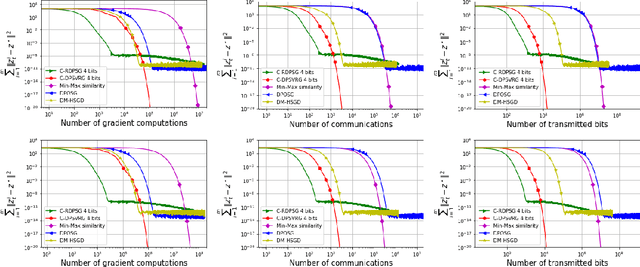
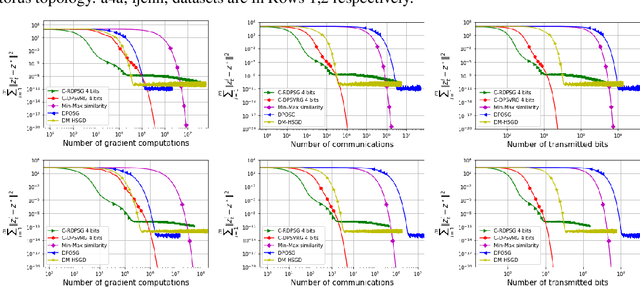
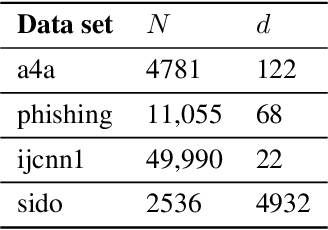
We propose two stochastic gradient algorithms to solve a class of saddle-point problems in a decentralized setting (without a central server). The proposed algorithms are the first to achieve sub-linear/linear computation and communication complexities using respectively stochastic gradient/stochastic variance reduced gradient oracles with compressed information exchange to solve non-smooth strongly-convex strongly-concave saddle-point problems in decentralized setting. Our first algorithm is a Restart-based Decentralized Proximal Stochastic Gradient method with Compression (C-RDPSG) for general stochastic settings. We provide rigorous theoretical guarantees of C-RDPSG with gradient computation complexity and communication complexity of order $\mathcal{O}( (1+\delta)^4 \frac{1}{L^2}{\kappa_f^2}\kappa_g^2 \frac{1}{\epsilon} )$, to achieve an $\epsilon$-accurate saddle-point solution, where $\delta$ denotes the compression factor, $\kappa_f$ and $\kappa_g$ denote respectively the condition numbers of objective function and communication graph, and $L$ denotes the smoothness parameter of the smooth part of the objective function. Next, we present a Decentralized Proximal Stochastic Variance Reduced Gradient algorithm with Compression (C-DPSVRG) for finite sum setting which exhibits gradient computation complexity and communication complexity of order $\mathcal{O}((1+\delta)\kappa_f^2 \kappa_g \log(\frac{1}{\epsilon}))$. Extensive numerical experiments show competitive performance of the proposed algorithms and provide support to the theoretical results obtained.