MCDDPM: Multichannel Conditional Denoising Diffusion Model for Unsupervised Anomaly Detection in Brain MRI

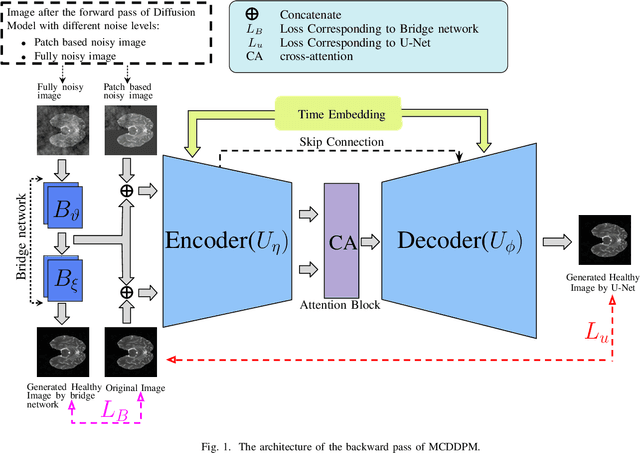
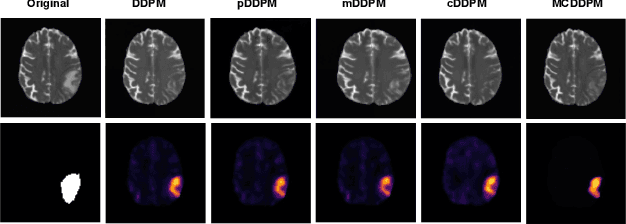
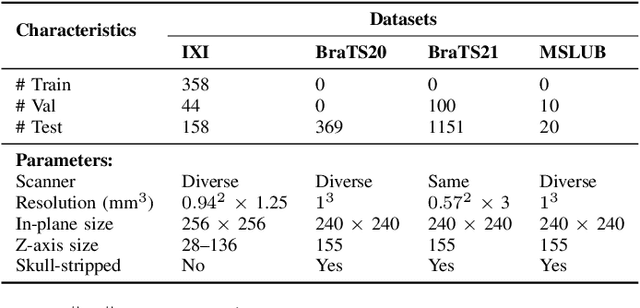
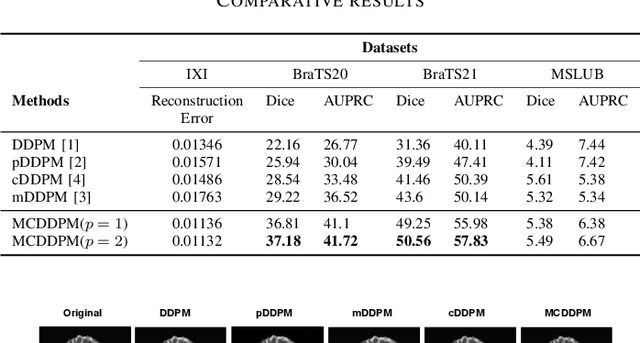
Detecting anomalies in brain MRI scans using supervised deep learning methods presents challenges due to anatomical diversity and labor-intensive requirement of pixel-level annotations. Generative models like Denoising Diffusion Probabilistic Model (DDPM) and their variants like pDDPM, mDDPM, cDDPM have recently emerged to be powerful alternatives to perform unsupervised anomaly detection in brain MRI scans. These methods leverage frame-level labels of healthy brains to generate healthy tissues in brain MRI scans. During inference, when an anomalous (or unhealthy) scan image is presented as an input, these models generate a healthy scan image corresponding to the input anomalous scan, and the difference map between the generated healthy scan image and the original anomalous scan image provide the necessary pixel level identification of abnormal tissues. The generated healthy images from the DDPM, pDDPM and mDDPM models however suffer from fidelity issues and contain artifacts that do not have medical significance. While cDDPM achieves slightly better fidelity and artifact suppression, it requires huge memory footprint and is computationally expensive than the other DDPM based models. In this work, we propose an improved version of DDPM called Multichannel Conditional Denoising Diffusion Probabilistic Model (MCDDPM) for unsupervised anomaly detection in brain MRI scans. Our proposed model achieves high fidelity by making use of additional information from the healthy images during the training process, enriching the representation power of DDPM models, with a computational cost and memory requirements on par with DDPM, pDDPM and mDDPM models. Experimental results on multiple datasets (e.g. BraTS20, BraTS21) demonstrate promising performance of the proposed method. The code is available at https://github.com/vivekkumartri/MCDDPM.

Switch and Conquer: Efficient Algorithms By Switching Stochastic Gradient Oracles For Decentralized Saddle Point Problems

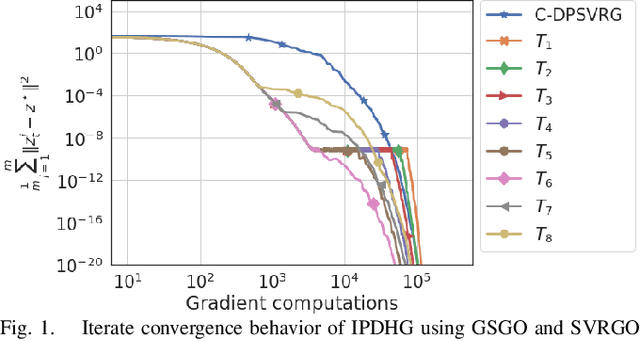
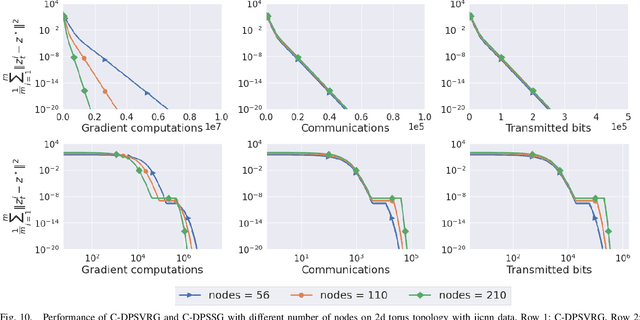
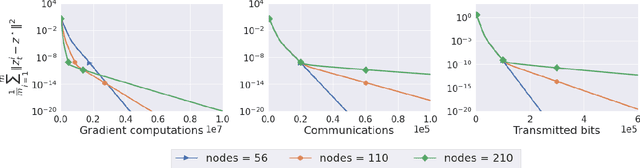
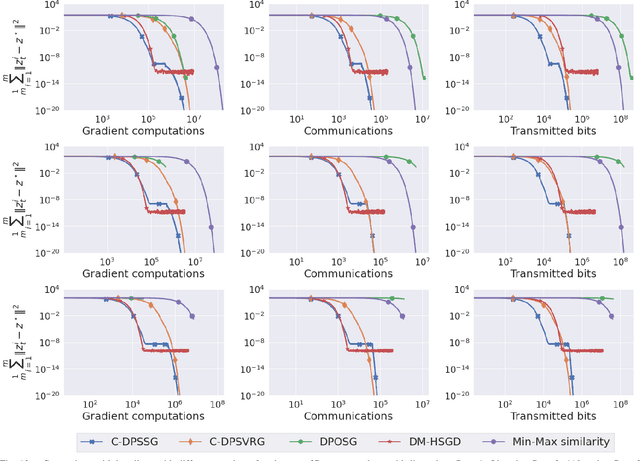
We consider a class of non-smooth strongly convex-strongly concave saddle point problems in a decentralized setting without a central server. To solve a consensus formulation of problems in this class, we develop an inexact primal dual hybrid gradient (inexact PDHG) procedure that allows generic gradient computation oracles to update the primal and dual variables. We first investigate the performance of inexact PDHG with stochastic variance reduction gradient (SVRG) oracle. Our numerical study uncovers a significant phenomenon of initial conservative progress of iterates of IPDHG with SVRG oracle. To tackle this, we develop a simple and effective switching idea, where a generalized stochastic gradient (GSG) computation oracle is employed to hasten the iterates' progress to a saddle point solution during the initial phase of updates, followed by a switch to the SVRG oracle at an appropriate juncture. The proposed algorithm is named Decentralized Proximal Switching Stochastic Gradient method with Compression (C-DPSSG), and is proven to converge to an $\epsilon$-accurate saddle point solution with linear rate. Apart from delivering highly accurate solutions, our study reveals that utilizing the best convergence phases of GSG and SVRG oracles makes C-DPSSG well suited for obtaining solutions of low/medium accuracy faster, useful for certain applications. Numerical experiments on two benchmark machine learning applications show C-DPSSG's competitive performance which validate our theoretical findings. The codes used in the experiments can be found \href{https://github.com/chhavisharma123/C-DPSSG-CDC2023}{here}.

Stochastic Gradient Methods with Compressed Communication for Decentralized Saddle Point Problems

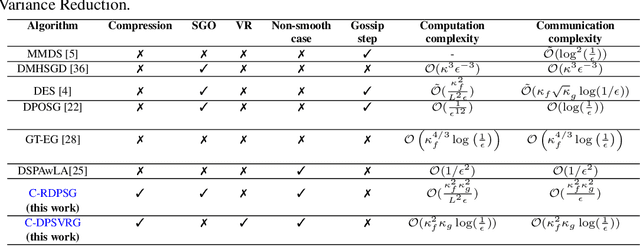
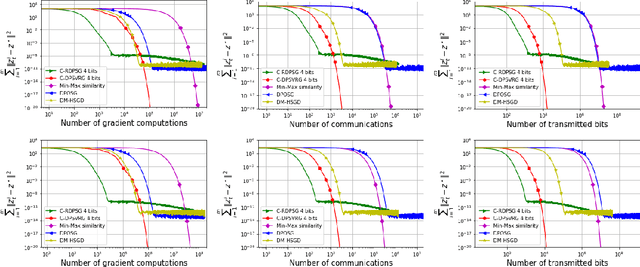
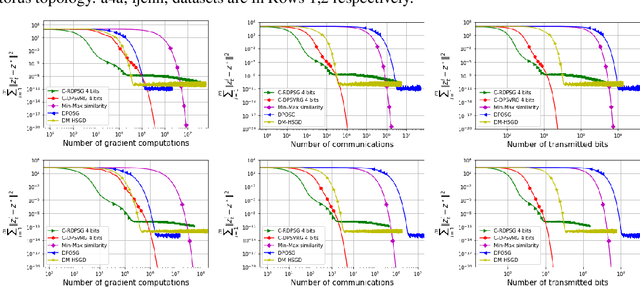
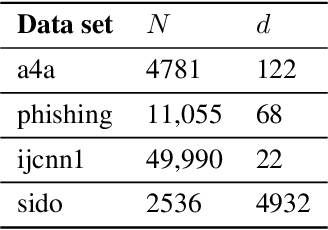
We propose two stochastic gradient algorithms to solve a class of saddle-point problems in a decentralized setting (without a central server). The proposed algorithms are the first to achieve sub-linear/linear computation and communication complexities using respectively stochastic gradient/stochastic variance reduced gradient oracles with compressed information exchange to solve non-smooth strongly-convex strongly-concave saddle-point problems in decentralized setting. Our first algorithm is a Restart-based Decentralized Proximal Stochastic Gradient method with Compression (C-RDPSG) for general stochastic settings. We provide rigorous theoretical guarantees of C-RDPSG with gradient computation complexity and communication complexity of order $\mathcal{O}( (1+\delta)^4 \frac{1}{L^2}{\kappa_f^2}\kappa_g^2 \frac{1}{\epsilon} )$, to achieve an $\epsilon$-accurate saddle-point solution, where $\delta$ denotes the compression factor, $\kappa_f$ and $\kappa_g$ denote respectively the condition numbers of objective function and communication graph, and $L$ denotes the smoothness parameter of the smooth part of the objective function. Next, we present a Decentralized Proximal Stochastic Variance Reduced Gradient algorithm with Compression (C-DPSVRG) for finite sum setting which exhibits gradient computation complexity and communication complexity of order $\mathcal{O}((1+\delta)\kappa_f^2 \kappa_g \log(\frac{1}{\epsilon}))$. Extensive numerical experiments show competitive performance of the proposed algorithms and provide support to the theoretical results obtained.

Gaussian Process Pseudo-Likelihood Models for Sequence Labeling

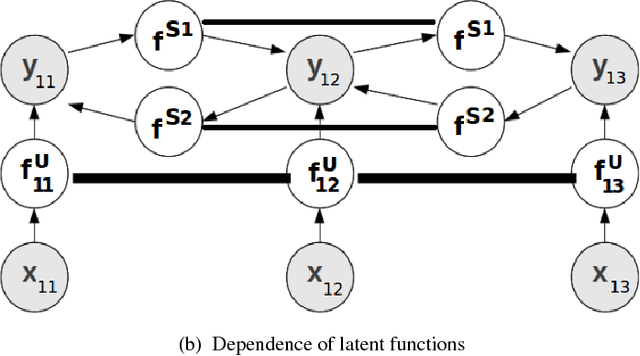
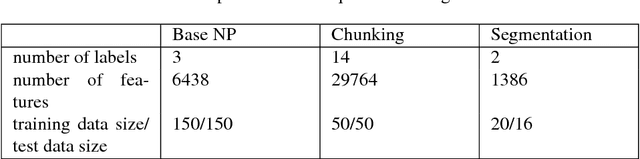
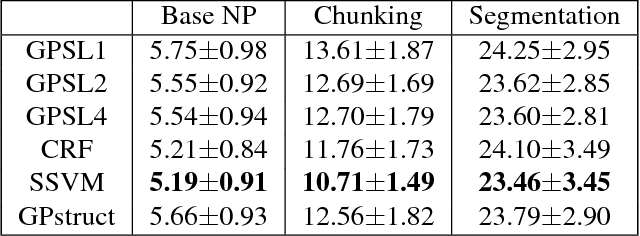
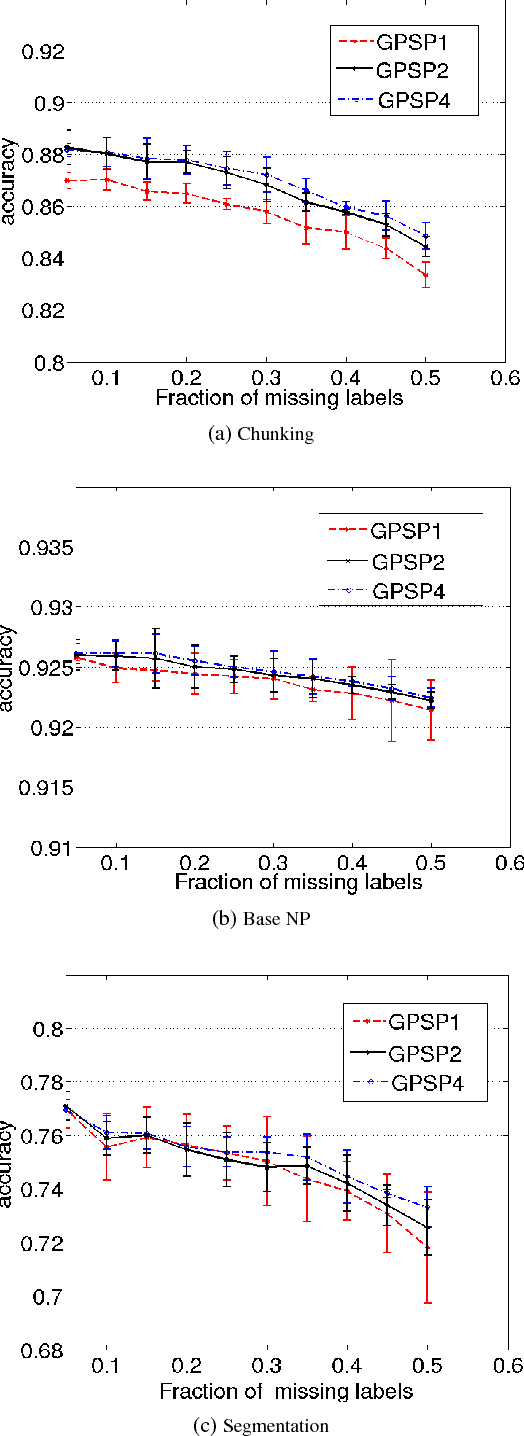
Several machine learning problems arising in natural language processing can be modeled as a sequence labeling problem. We provide Gaussian process models based on pseudo-likelihood approximation to perform sequence labeling. Gaussian processes (GPs) provide a Bayesian approach to learning in a kernel based framework. The pseudo-likelihood model enables one to capture long range dependencies among the output components of the sequence without becoming computationally intractable. We use an efficient variational Gaussian approximation method to perform inference in the proposed model. We also provide an iterative algorithm which can effectively make use of the information from the neighboring labels to perform prediction. The ability to capture long range dependencies makes the proposed approach useful for a wide range of sequence labeling problems. Numerical experiments on some sequence labeling data sets demonstrate the usefulness of the proposed approach.

An Empirical Evaluation of Sequence-Tagging Trainers

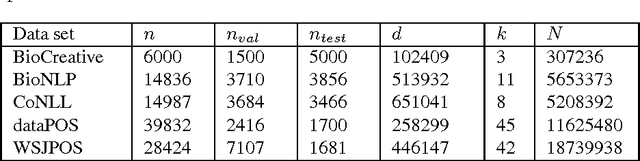
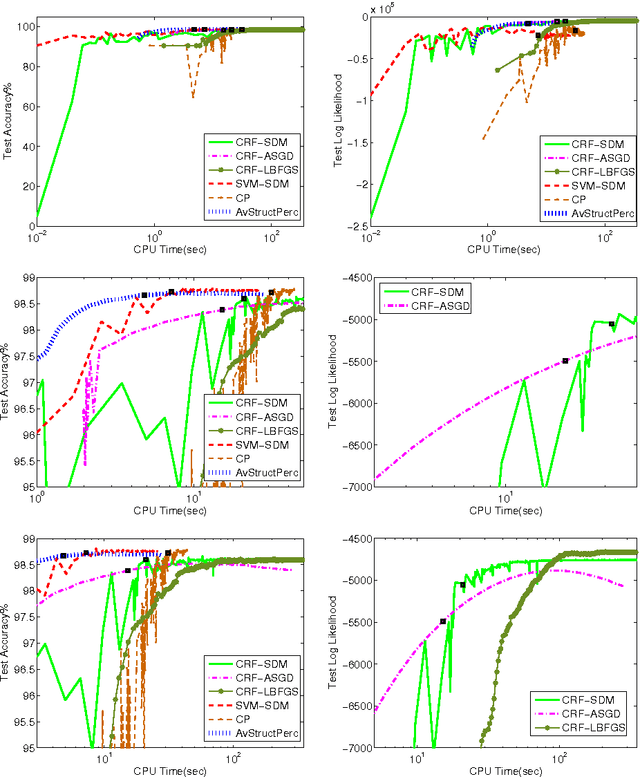
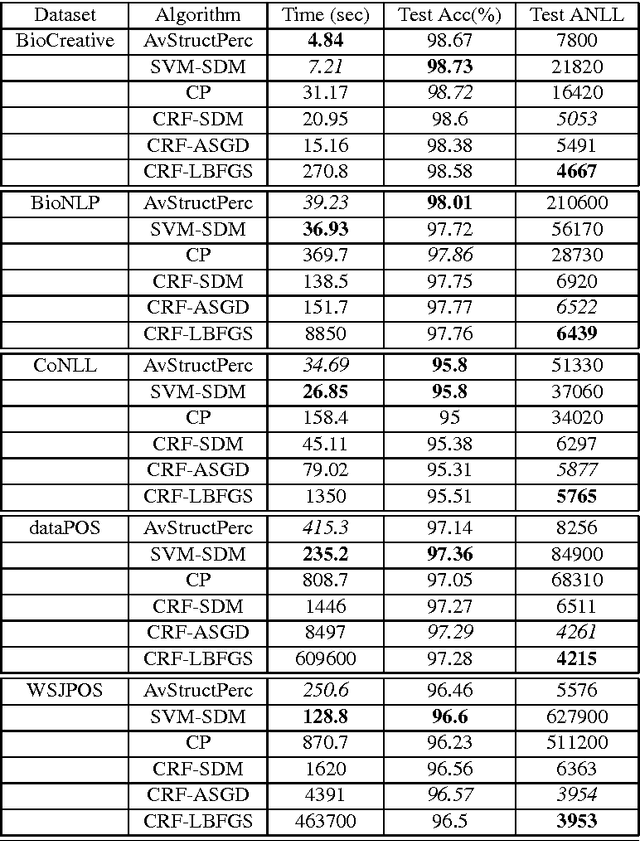
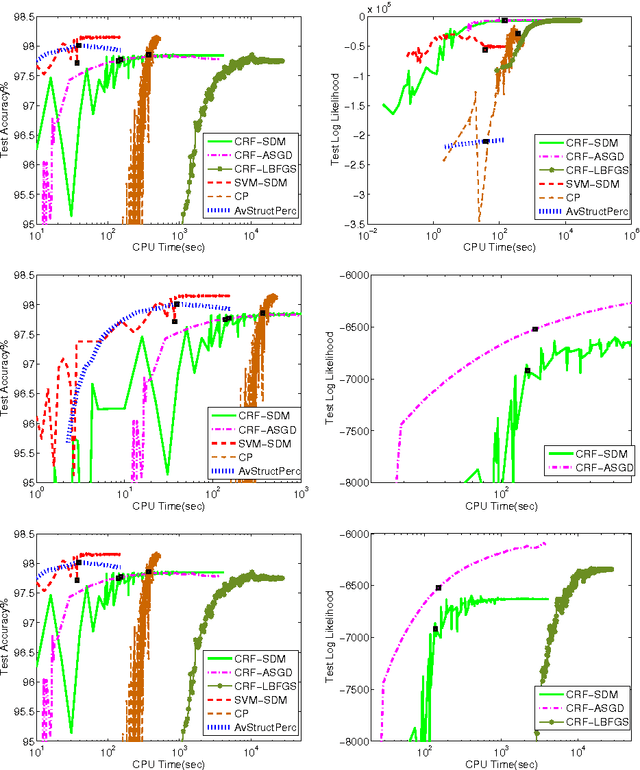
The task of assigning label sequences to a set of observed sequences is common in computational linguistics. Several models for sequence labeling have been proposed over the last few years. Here, we focus on discriminative models for sequence labeling. Many batch and online (updating model parameters after visiting each example) learning algorithms have been proposed in the literature. On large datasets, online algorithms are preferred as batch learning methods are slow. These online algorithms were designed to solve either a primal or a dual problem. However, there has been no systematic comparison of these algorithms in terms of their speed, generalization performance (accuracy/likelihood) and their ability to achieve steady state generalization performance fast. With this aim, we compare different algorithms and make recommendations, useful for a practitioner. We conclude that the selection of an algorithm for sequence labeling depends on the evaluation criterion used and its implementation simplicity.

Large Margin Semi-supervised Structured Output Learning

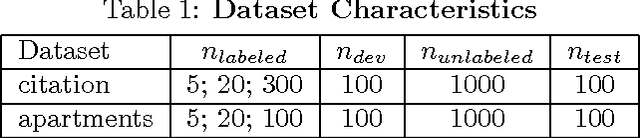
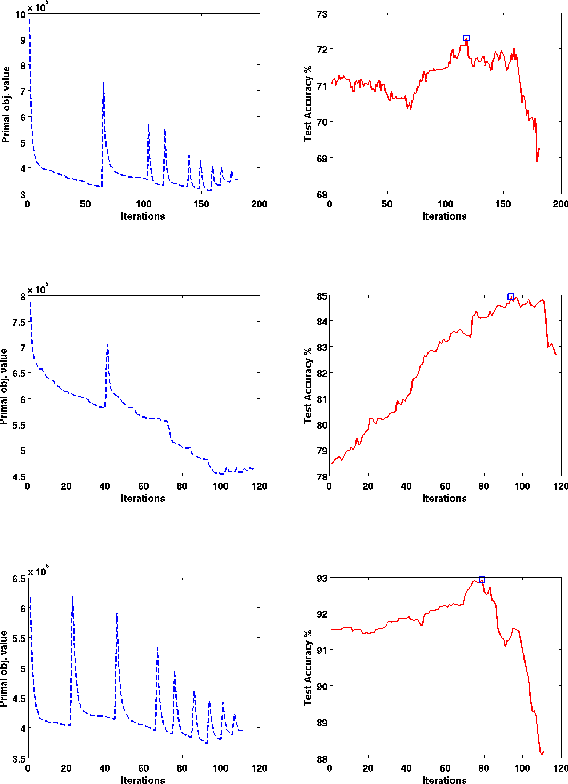
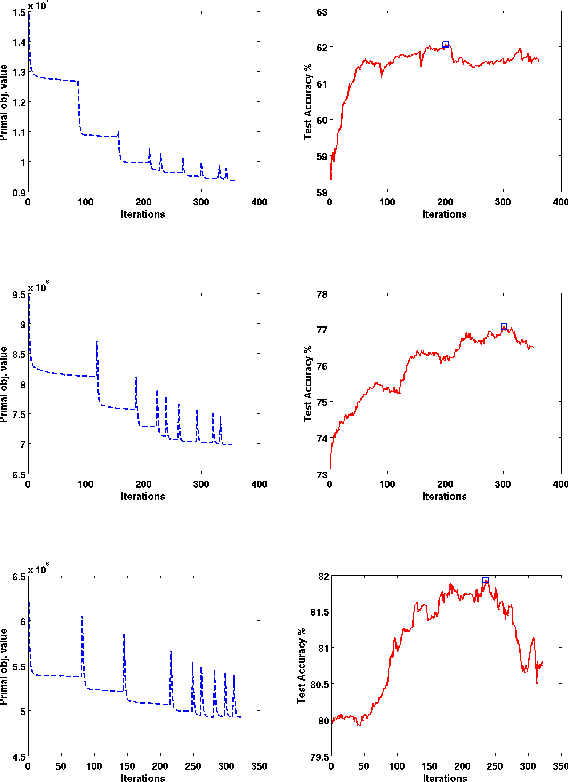
In structured output learning, obtaining labelled data for real-world applications is usually costly, while unlabelled examples are available in abundance. Semi-supervised structured classification has been developed to handle large amounts of unlabelled structured data. In this work, we consider semi-supervised structural SVMs with domain constraints. The optimization problem, which in general is not convex, contains the loss terms associated with the labelled and unlabelled examples along with the domain constraints. We propose a simple optimization approach, which alternates between solving a supervised learning problem and a constraint matching problem. Solving the constraint matching problem is difficult for structured prediction, and we propose an efficient and effective hill-climbing method to solve it. The alternating optimization is carried out within a deterministic annealing framework, which helps in effective constraint matching, and avoiding local minima which are not very useful. The algorithm is simple to implement and achieves comparable generalization performance on benchmark datasets.