Large Margin Semi-supervised Structured Output Learning
Paper and Code
Nov 09, 2013
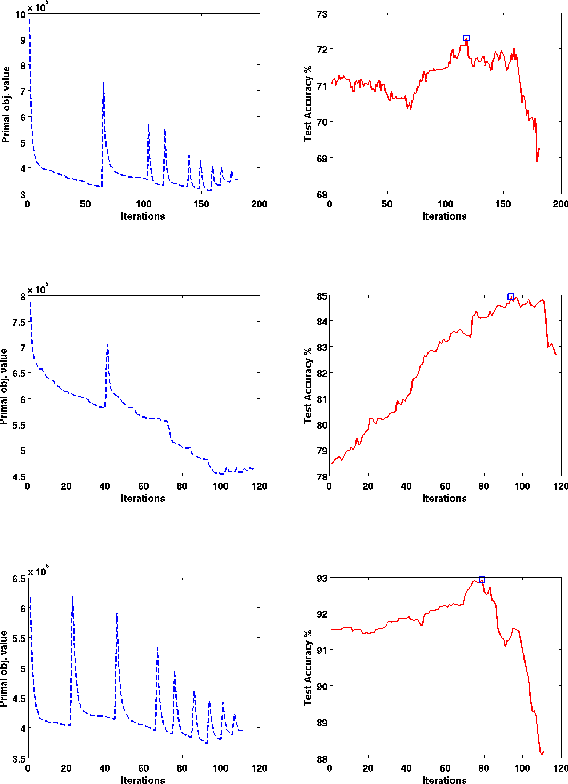

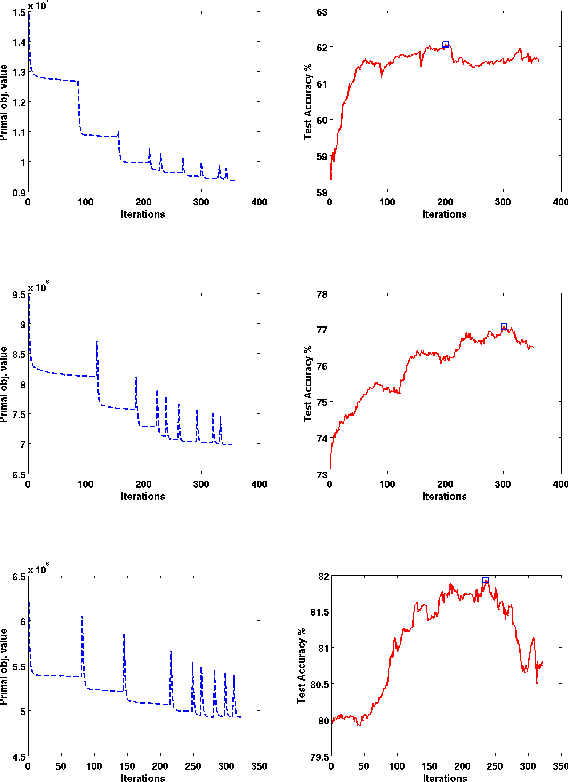
In structured output learning, obtaining labelled data for real-world applications is usually costly, while unlabelled examples are available in abundance. Semi-supervised structured classification has been developed to handle large amounts of unlabelled structured data. In this work, we consider semi-supervised structural SVMs with domain constraints. The optimization problem, which in general is not convex, contains the loss terms associated with the labelled and unlabelled examples along with the domain constraints. We propose a simple optimization approach, which alternates between solving a supervised learning problem and a constraint matching problem. Solving the constraint matching problem is difficult for structured prediction, and we propose an efficient and effective hill-climbing method to solve it. The alternating optimization is carried out within a deterministic annealing framework, which helps in effective constraint matching, and avoiding local minima which are not very useful. The algorithm is simple to implement and achieves comparable generalization performance on benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge