S. Sundararajan
Distributed Newton Methods for Deep Neural Networks
Feb 01, 2018Abstract:Deep learning involves a difficult non-convex optimization problem with a large number of weights between any two adjacent layers of a deep structure. To handle large data sets or complicated networks, distributed training is needed, but the calculation of function, gradient, and Hessian is expensive. In particular, the communication and the synchronization cost may become a bottleneck. In this paper, we focus on situations where the model is distributedly stored, and propose a novel distributed Newton method for training deep neural networks. By variable and feature-wise data partitions, and some careful designs, we are able to explicitly use the Jacobian matrix for matrix-vector products in the Newton method. Some techniques are incorporated to reduce the running time as well as the memory consumption. First, to reduce the communication cost, we propose a diagonalization method such that an approximate Newton direction can be obtained without communication between machines. Second, we consider subsampled Gauss-Newton matrices for reducing the running time as well as the communication cost. Third, to reduce the synchronization cost, we terminate the process of finding an approximate Newton direction even though some nodes have not finished their tasks. Details of some implementation issues in distributed environments are thoroughly investigated. Experiments demonstrate that the proposed method is effective for the distributed training of deep neural networks. In compared with stochastic gradient methods, it is more robust and may give better test accuracy.
A distributed block coordinate descent method for training $l_1$ regularized linear classifiers
Mar 16, 2015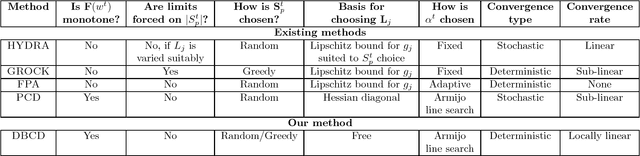
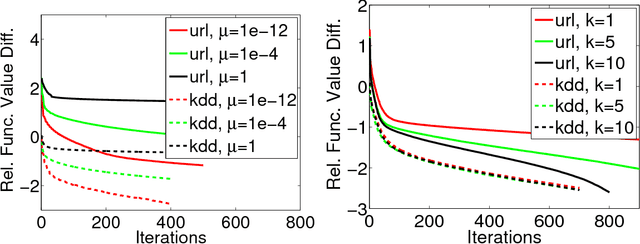

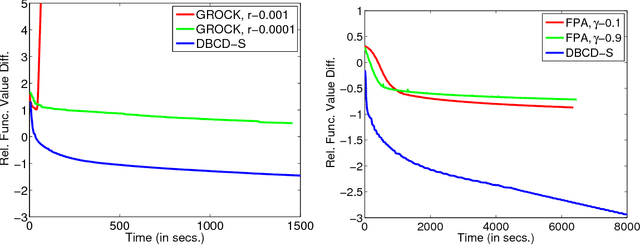
Abstract:Distributed training of $l_1$ regularized classifiers has received great attention recently. Most existing methods approach this problem by taking steps obtained from approximating the objective by a quadratic approximation that is decoupled at the individual variable level. These methods are designed for multicore and MPI platforms where communication costs are low. They are inefficient on systems such as Hadoop running on a cluster of commodity machines where communication costs are substantial. In this paper we design a distributed algorithm for $l_1$ regularization that is much better suited for such systems than existing algorithms. A careful cost analysis is used to support these points and motivate our method. The main idea of our algorithm is to do block optimization of many variables on the actual objective function within each computing node; this increases the computational cost per step that is matched with the communication cost, and decreases the number of outer iterations, thus yielding a faster overall method. Distributed Gauss-Seidel and Gauss-Southwell greedy schemes are used for choosing variables to update in each step. We establish global convergence theory for our algorithm, including Q-linear rate of convergence. Experiments on two benchmark problems show our method to be much faster than existing methods.
An efficient distributed learning algorithm based on effective local functional approximations
Mar 16, 2015



Abstract:Scalable machine learning over big data is an important problem that is receiving a lot of attention in recent years. On popular distributed environments such as Hadoop running on a cluster of commodity machines, communication costs are substantial and algorithms need to be designed suitably considering those costs. In this paper we give a novel approach to the distributed training of linear classifiers (involving smooth losses and L2 regularization) that is designed to reduce the total communication costs. At each iteration, the nodes minimize locally formed approximate objective functions; then the resulting minimizers are combined to form a descent direction to move. Our approach gives a lot of freedom in the formation of the approximate objective function as well as in the choice of methods to solve them. The method is shown to have $O(log(1/\epsilon))$ time convergence. The method can be viewed as an iterative parameter mixing method. A special instantiation yields a parallel stochastic gradient descent method with strong convergence. When communication times between nodes are large, our method is much faster than the Terascale method (Agarwal et al., 2011), which is a state of the art distributed solver based on the statistical query model (Chuet al., 2006) that computes function and gradient values in a distributed fashion. We also evaluate against other recent distributed methods and demonstrate superior performance of our method.
A Distributed Algorithm for Training Nonlinear Kernel Machines
May 18, 2014



Abstract:This paper concerns the distributed training of nonlinear kernel machines on Map-Reduce. We show that a re-formulation of Nystr\"om approximation based solution which is solved using gradient based techniques is well suited for this, especially when it is necessary to work with a large number of basis points. The main advantages of this approach are: avoidance of computing the pseudo-inverse of the kernel sub-matrix corresponding to the basis points; simplicity and efficiency of the distributed part of the computations; and, friendliness to stage-wise addition of basis points. We implement the method using an AllReduce tree on Hadoop and demonstrate its value on a few large benchmark datasets.
An Empirical Evaluation of Sequence-Tagging Trainers
Nov 11, 2013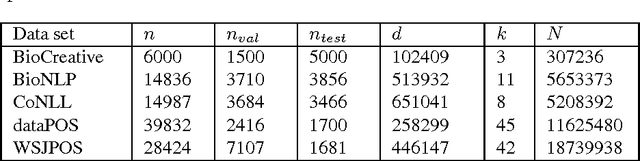
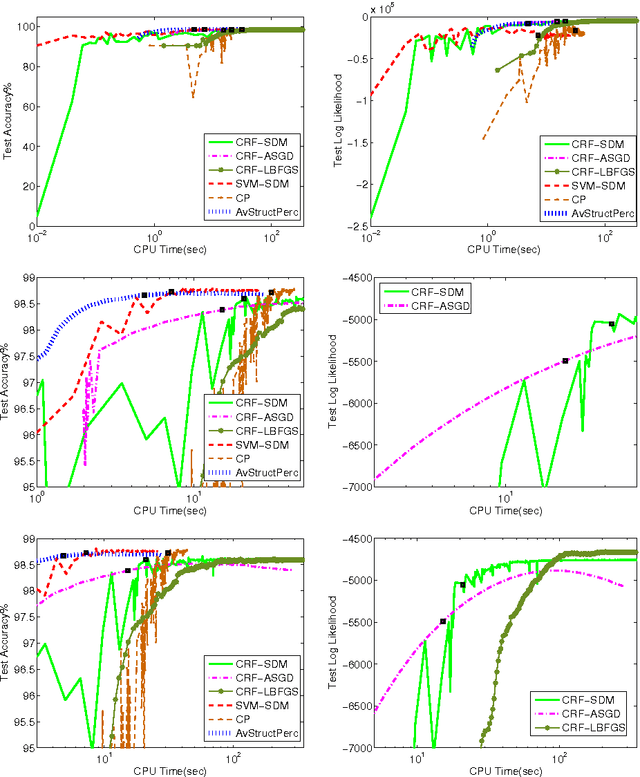
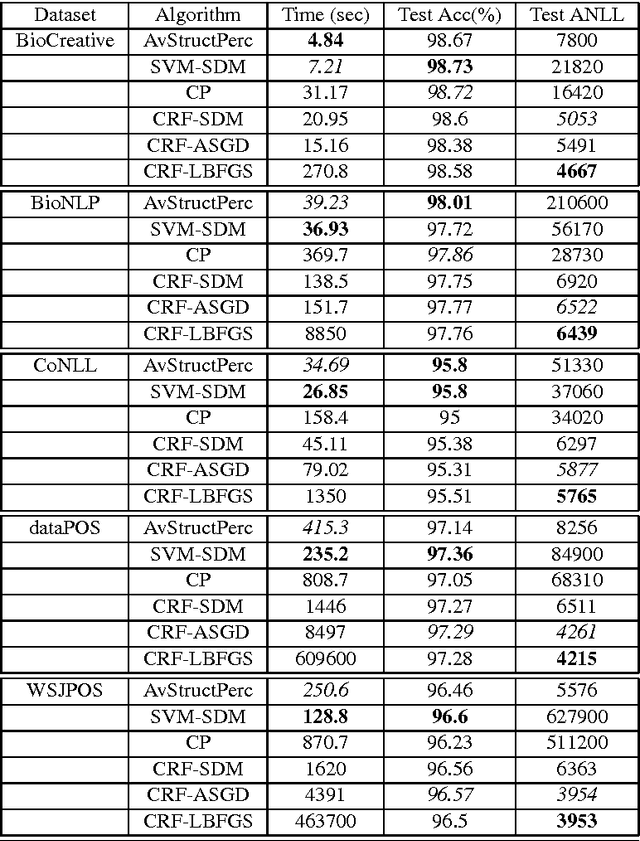
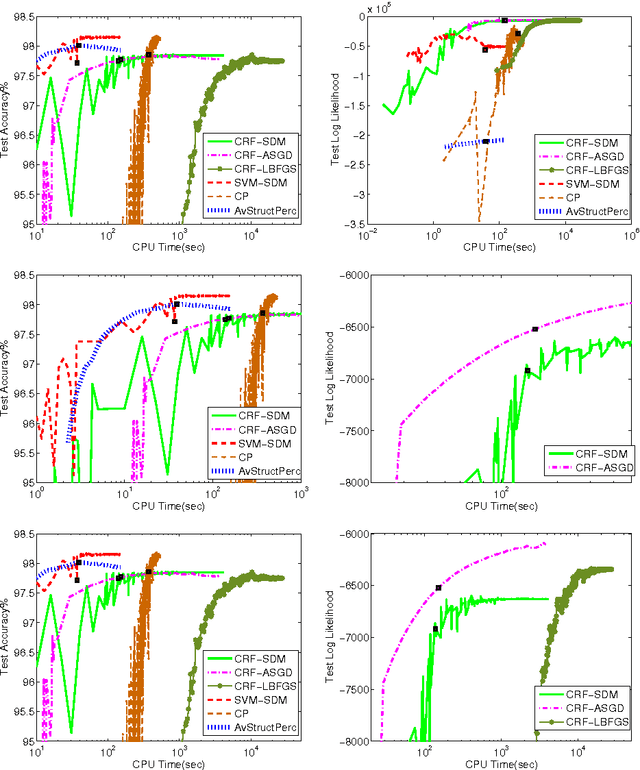
Abstract:The task of assigning label sequences to a set of observed sequences is common in computational linguistics. Several models for sequence labeling have been proposed over the last few years. Here, we focus on discriminative models for sequence labeling. Many batch and online (updating model parameters after visiting each example) learning algorithms have been proposed in the literature. On large datasets, online algorithms are preferred as batch learning methods are slow. These online algorithms were designed to solve either a primal or a dual problem. However, there has been no systematic comparison of these algorithms in terms of their speed, generalization performance (accuracy/likelihood) and their ability to achieve steady state generalization performance fast. With this aim, we compare different algorithms and make recommendations, useful for a practitioner. We conclude that the selection of an algorithm for sequence labeling depends on the evaluation criterion used and its implementation simplicity.
A Parallel SGD method with Strong Convergence
Nov 04, 2013
Abstract:This paper proposes a novel parallel stochastic gradient descent (SGD) method that is obtained by applying parallel sets of SGD iterations (each set operating on one node using the data residing in it) for finding the direction in each iteration of a batch descent method. The method has strong convergence properties. Experiments on datasets with high dimensional feature spaces show the value of this method.
Mechanism Design for Cost Optimal PAC Learning in the Presence of Strategic Noisy Annotators
Oct 16, 2012
Abstract:We consider the problem of Probably Approximate Correct (PAC) learning of a binary classifier from noisy labeled examples acquired from multiple annotators (each characterized by a respective classification noise rate). First, we consider the complete information scenario, where the learner knows the noise rates of all the annotators. For this scenario, we derive sample complexity bound for the Minimum Disagreement Algorithm (MDA) on the number of labeled examples to be obtained from each annotator. Next, we consider the incomplete information scenario, where each annotator is strategic and holds the respective noise rate as a private information. For this scenario, we design a cost optimal procurement auction mechanism along the lines of Myerson's optimal auction design framework in a non-trivial manner. This mechanism satisfies incentive compatibility property, thereby facilitating the learner to elicit true noise rates of all the annotators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge