Kent Loong Tan
Newton Methods for Convolutional Neural Networks
Nov 14, 2018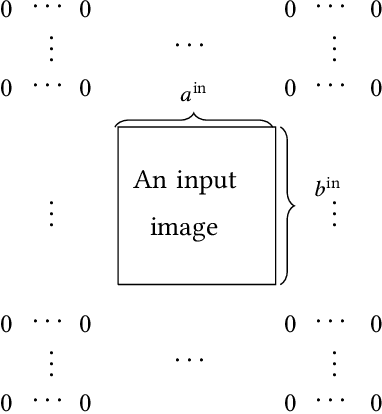



Abstract:Deep learning involves a difficult non-convex optimization problem, which is often solved by stochastic gradient (SG) methods. While SG is usually effective, it may not be robust in some situations. Recently, Newton methods have been investigated as an alternative optimization technique, but nearly all existing studies consider only fully-connected feedforward neural networks. They do not investigate other types of networks such as Convolutional Neural Networks (CNN), which are more commonly used in deep-learning applications. One reason is that Newton methods for CNN involve complicated operations, and so far no works have conducted a thorough investigation. In this work, we give details of all building blocks including function, gradient, and Jacobian evaluation, and Gauss-Newton matrix-vector products. These basic components are very important because with them further developments of Newton methods for CNN become possible. We show that an efficient MATLAB implementation can be done in just several hundred lines of code and demonstrate that the Newton method gives competitive test accuracy.
Distributed Newton Methods for Deep Neural Networks
Feb 01, 2018Abstract:Deep learning involves a difficult non-convex optimization problem with a large number of weights between any two adjacent layers of a deep structure. To handle large data sets or complicated networks, distributed training is needed, but the calculation of function, gradient, and Hessian is expensive. In particular, the communication and the synchronization cost may become a bottleneck. In this paper, we focus on situations where the model is distributedly stored, and propose a novel distributed Newton method for training deep neural networks. By variable and feature-wise data partitions, and some careful designs, we are able to explicitly use the Jacobian matrix for matrix-vector products in the Newton method. Some techniques are incorporated to reduce the running time as well as the memory consumption. First, to reduce the communication cost, we propose a diagonalization method such that an approximate Newton direction can be obtained without communication between machines. Second, we consider subsampled Gauss-Newton matrices for reducing the running time as well as the communication cost. Third, to reduce the synchronization cost, we terminate the process of finding an approximate Newton direction even though some nodes have not finished their tasks. Details of some implementation issues in distributed environments are thoroughly investigated. Experiments demonstrate that the proposed method is effective for the distributed training of deep neural networks. In compared with stochastic gradient methods, it is more robust and may give better test accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge