A spectral method for multi-view subspace learning using the product of projections

Multi-view data provides complementary information on the same set of observations, with multi-omics and multimodal sensor data being common examples. Analyzing such data typically requires distinguishing between shared (joint) and unique (individual) signal subspaces from noisy, high-dimensional measurements. Despite many proposed methods, the conditions for reliably identifying joint and individual subspaces remain unclear. We rigorously quantify these conditions, which depend on the ratio of the signal rank to the ambient dimension, principal angles between true subspaces, and noise levels. Our approach characterizes how spectrum perturbations of the product of projection matrices, derived from each view's estimated subspaces, affect subspace separation. Using these insights, we provide an easy-to-use and scalable estimation algorithm. In particular, we employ rotational bootstrap and random matrix theory to partition the observed spectrum into joint, individual, and noise subspaces. Diagnostic plots visualize this partitioning, providing practical and interpretable insights into the estimation performance. In simulations, our method estimates joint and individual subspaces more accurately than existing approaches. Applications to multi-omics data from colorectal cancer patients and nutrigenomic study of mice demonstrate improved performance in downstream predictive tasks.

An Asymptotically Optimal Coordinate Descent Algorithm for Learning Bayesian Networks from Gaussian Models

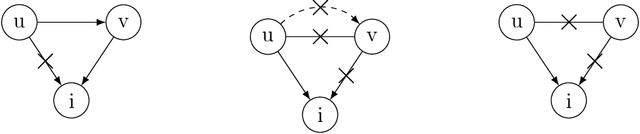
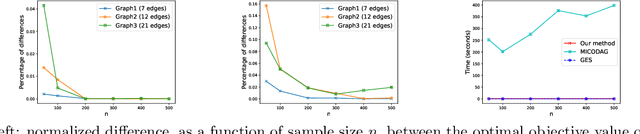
This paper studies the problem of learning Bayesian networks from continuous observational data, generated according to a linear Gaussian structural equation model. We consider an $\ell_0$-penalized maximum likelihood estimator for this problem which is known to have favorable statistical properties but is computationally challenging to solve, especially for medium-sized Bayesian networks. We propose a new coordinate descent algorithm to approximate this estimator and prove several remarkable properties of our procedure: the algorithm converges to a coordinate-wise minimum, and despite the non-convexity of the loss function, as the sample size tends to infinity, the objective value of the coordinate descent solution converges to the optimal objective value of the $\ell_0$-penalized maximum likelihood estimator. Finite-sample optimality and statistical consistency guarantees are also established. To the best of our knowledge, our proposal is the first coordinate descent procedure endowed with optimality and statistical guarantees in the context of learning Bayesian networks. Numerical experiments on synthetic and real data demonstrate that our coordinate descent method can obtain near-optimal solutions while being scalable.

Extremal graphical modeling with latent variables

Extremal graphical models encode the conditional independence structure of multivariate extremes and provide a powerful tool for quantifying the risk of rare events. Prior work on learning these graphs from data has focused on the setting where all relevant variables are observed. For the popular class of H\"usler-Reiss models, we propose the \texttt{eglatent} method, a tractable convex program for learning extremal graphical models in the presence of latent variables. Our approach decomposes the H\"usler-Reiss precision matrix into a sparse component encoding the graphical structure among the observed variables after conditioning on the latent variables, and a low-rank component encoding the effect of a few latent variables on the observed variables. We provide finite-sample guarantees of \texttt{eglatent} and show that it consistently recovers the conditional graph as well as the number of latent variables. We highlight the improved performances of our approach on synthetic and real data.

Causality-oriented robustness: exploiting general additive interventions

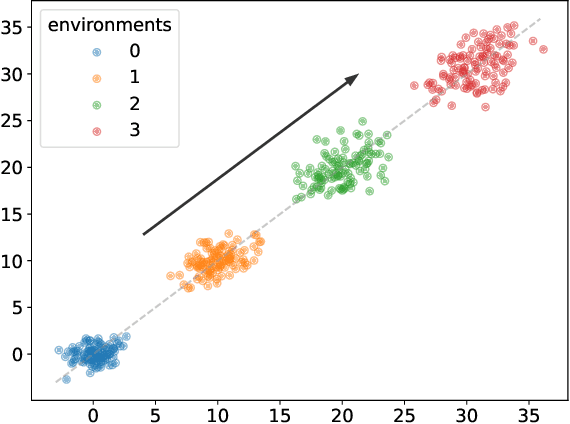
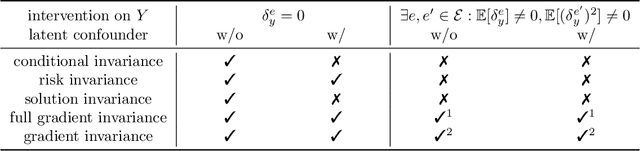
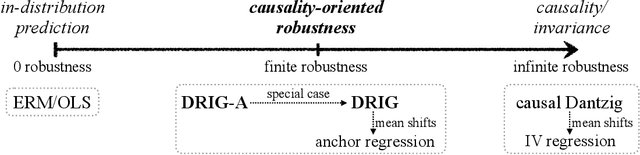
Since distribution shifts are common in real-world applications, there is a pressing need for developing prediction models that are robust against such shifts. Existing frameworks, such as empirical risk minimization or distributionally robust optimization, either lack generalizability for unseen distributions or rely on postulated distance measures. Alternatively, causality offers a data-driven and structural perspective to robust predictions. However, the assumptions necessary for causal inference can be overly stringent, and the robustness offered by such causal models often lacks flexibility. In this paper, we focus on causality-oriented robustness and propose Distributional Robustness via Invariant Gradients (DRIG), a method that exploits general additive interventions in training data for robust predictions against unseen interventions, and naturally interpolates between in-distribution prediction and causality. In a linear setting, we prove that DRIG yields predictions that are robust among a data-dependent class of distribution shifts. Furthermore, we show that our framework includes anchor regression (Rothenh\"ausler et al.\ 2021) as a special case, and that it yields prediction models that protect against more diverse perturbations. We extend our approach to the semi-supervised domain adaptation setting to further improve prediction performance. Finally, we empirically validate our methods on synthetic simulations and on single-cell data.

Characterization and Greedy Learning of Gaussian Structural Causal Models under Unknown Interventions

We consider the problem of recovering the causal structure underlying observations from different experimental conditions when the targets of the interventions in each experiment are unknown. We assume a linear structural causal model with additive Gaussian noise and consider interventions that perturb their targets while maintaining the causal relationships in the system. Different models may entail the same distributions, offering competing causal explanations for the given observations. We fully characterize this equivalence class and offer identifiability results, which we use to derive a greedy algorithm called GnIES to recover the equivalence class of the data-generating model without knowledge of the intervention targets. In addition, we develop a novel procedure to generate semi-synthetic data sets with known causal ground truth but distributions closely resembling those of a real data set of choice. We leverage this procedure and evaluate the performance of GnIES on synthetic, real, and semi-synthetic data sets. Despite the strong Gaussian distributional assumption, GnIES is robust to an array of model violations and competitive in recovering the causal structure in small- to large-sample settings. We provide, in the Python packages "gnies" and "sempler", implementations of GnIES and our semi-synthetic data generation procedure.

Provable concept learning for interpretable predictions using variational inference

In safety critical applications, practitioners are reluctant to trust neural networks when no interpretable explanations are available. Many attempts to provide such explanations revolve around pixel level attributions or use previously known concepts. In this paper we aim to provide explanations by provably identifying \emph{high-level, previously unknown concepts}. To this end, we propose a probabilistic modeling framework to derive (C)oncept (L)earning and (P)rediction (CLAP) -- a VAE-based classifier that uses visually interpretable concepts as linear predictors. Assuming that the data generating mechanism involves predictive concepts, we prove that our method is able to identify them while attaining optimal classification accuracy. We use synthetic experiments for validation, and also show that on real-world (PlantVillage and ChestXRay) datasets, CLAP effectively discovers interpretable factors for classifying diseases.

A Fast Non-parametric Approach for Causal Structure Learning in Polytrees

We study the problem of causal structure learning with no assumptions on the functional relationships and noise. We develop DAG-FOCI, a computationally fast algorithm for this setting that is based on the FOCI variable selection algorithm in \cite{azadkia2019simple}. DAG-FOCI requires no tuning parameter and outputs the parents and the Markov boundary of a response variable of interest. We provide high-dimensional guarantees of our procedure when the underlying graph is a polytree. Furthermore, we demonstrate the applicability of DAG-FOCI on real data from computational biology \cite{sachs2005causal} and illustrate the robustness of our methods to violations of assumptions.

Learning Exponential Family Graphical Models with Latent Variables using Regularized Conditional Likelihood

Fitting a graphical model to a collection of random variables given sample observations is a challenging task if the observed variables are influenced by latent variables, which can induce significant confounding statistical dependencies among the observed variables. We present a new convex relaxation framework based on regularized conditional likelihood for latent-variable graphical modeling in which the conditional distribution of the observed variables conditioned on the latent variables is given by an exponential family graphical model. In comparison to previously proposed tractable methods that proceed by characterizing the marginal distribution of the observed variables, our approach is applicable in a broader range of settings as it does not require knowledge about the specific form of distribution of the latent variables and it can be specialized to yield tractable approaches to problems in which the observed data are not well-modeled as Gaussian. We demonstrate the utility and flexibility of our framework via a series of numerical experiments on synthetic as well as real data.