A spectral method for multi-view subspace learning using the product of projections

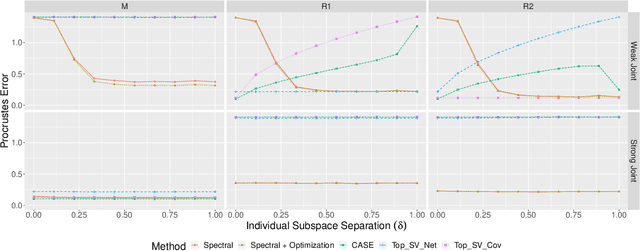
Multi-view data provides complementary information on the same set of observations, with multi-omics and multimodal sensor data being common examples. Analyzing such data typically requires distinguishing between shared (joint) and unique (individual) signal subspaces from noisy, high-dimensional measurements. Despite many proposed methods, the conditions for reliably identifying joint and individual subspaces remain unclear. We rigorously quantify these conditions, which depend on the ratio of the signal rank to the ambient dimension, principal angles between true subspaces, and noise levels. Our approach characterizes how spectrum perturbations of the product of projection matrices, derived from each view's estimated subspaces, affect subspace separation. Using these insights, we provide an easy-to-use and scalable estimation algorithm. In particular, we employ rotational bootstrap and random matrix theory to partition the observed spectrum into joint, individual, and noise subspaces. Diagnostic plots visualize this partitioning, providing practical and interpretable insights into the estimation performance. In simulations, our method estimates joint and individual subspaces more accurately than existing approaches. Applications to multi-omics data from colorectal cancer patients and nutrigenomic study of mice demonstrate improved performance in downstream predictive tasks.

GlucoBench: Curated List of Continuous Glucose Monitoring Datasets with Prediction Benchmarks

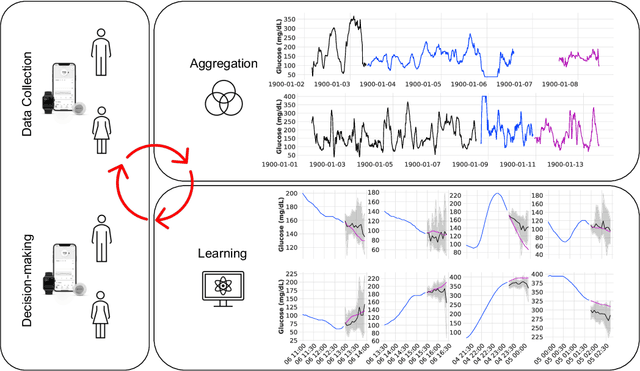
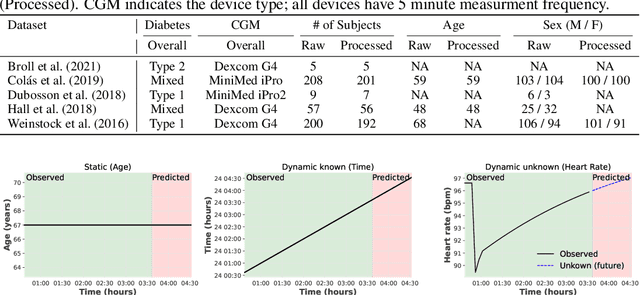
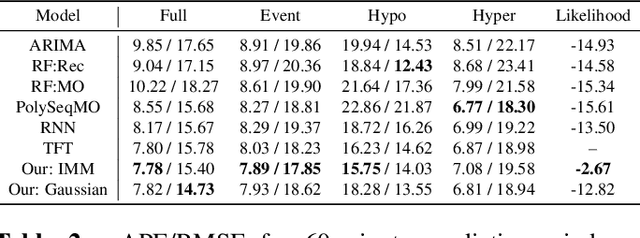
The rising rates of diabetes necessitate innovative methods for its management. Continuous glucose monitors (CGM) are small medical devices that measure blood glucose levels at regular intervals providing insights into daily patterns of glucose variation. Forecasting of glucose trajectories based on CGM data holds the potential to substantially improve diabetes management, by both refining artificial pancreas systems and enabling individuals to make adjustments based on predictions to maintain optimal glycemic range.Despite numerous methods proposed for CGM-based glucose trajectory prediction, these methods are typically evaluated on small, private datasets, impeding reproducibility, further research, and practical adoption. The absence of standardized prediction tasks and systematic comparisons between methods has led to uncoordinated research efforts, obstructing the identification of optimal tools for tackling specific challenges. As a result, only a limited number of prediction methods have been implemented in clinical practice. To address these challenges, we present a comprehensive resource that provides (1) a consolidated repository of curated publicly available CGM datasets to foster reproducibility and accessibility; (2) a standardized task list to unify research objectives and facilitate coordinated efforts; (3) a set of benchmark models with established baseline performance, enabling the research community to objectively gauge new methods' efficacy; and (4) a detailed analysis of performance-influencing factors for model development. We anticipate these resources to propel collaborative research endeavors in the critical domain of CGM-based glucose predictions. {Our code is available online at github.com/IrinaStatsLab/GlucoBench.

Learning Joint and Individual Structure in Network Data with Covariates

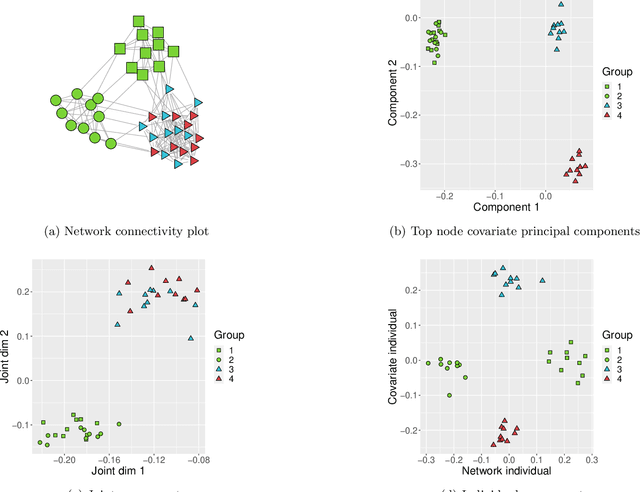
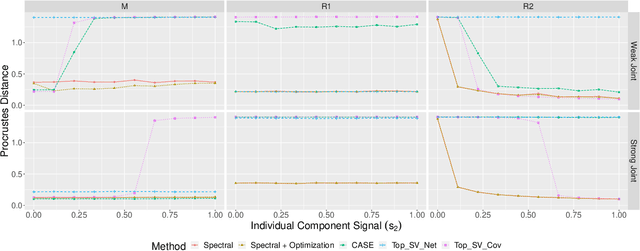
Datasets consisting of a network and covariates associated with its vertices have become ubiquitous. One problem pertaining to this type of data is to identify information unique to the network, information unique to the vertex covariates and information that is shared between the network and the vertex covariates. Existing techniques for network data and vertex covariates focus on capturing structure that is shared but are usually not able to differentiate structure that is unique to each dataset. This work formulates a low-rank model that simultaneously captures joint and individual information in network data with vertex covariates. A two-step estimation procedure is proposed, composed of an efficient spectral method followed by a refinement optimization step. Theoretically, we show that the spectral method is able to consistently recover the joint and individual components under a general signal-plus-noise model. Simulations and real data examples demonstrate the ability of the methods to recover accurate and interpretable components. In particular, the application of the methodology to a food trade network between countries with economic, developmental and geographical country-level indicators as covariates yields joint and individual factors that explain the trading patterns.

Gluformer: Transformer-Based Personalized Glucose Forecasting with Uncertainty Quantification

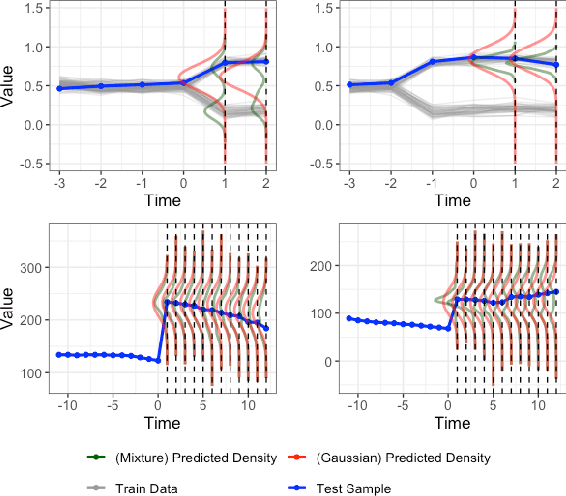
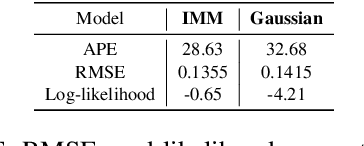
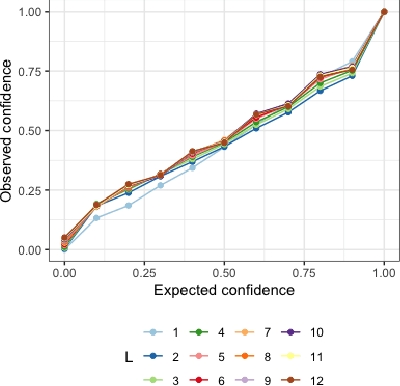
Deep learning models achieve state-of-the art results in predicting blood glucose trajectories, with a wide range of architectures being proposed. However, the adaptation of such models in clinical practice is slow, largely due to the lack of uncertainty quantification of provided predictions. In this work, we propose to model the future glucose trajectory conditioned on the past as an infinite mixture of basis distributions (i.e., Gaussian, Laplace, etc.). This change allows us to learn the uncertainty and predict more accurately in the cases when the trajectory has a heterogeneous or multi-modal distribution. To estimate the parameters of the predictive distribution, we utilize the Transformer architecture. We empirically demonstrate the superiority of our method over existing state-of-the-art techniques both in terms of accuracy and uncertainty on the synthetic and benchmark glucose data sets.

Double-matched matrix decomposition for multi-view data

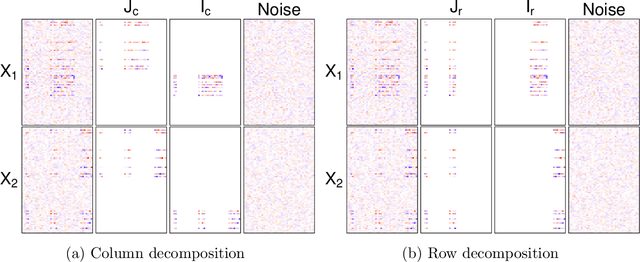
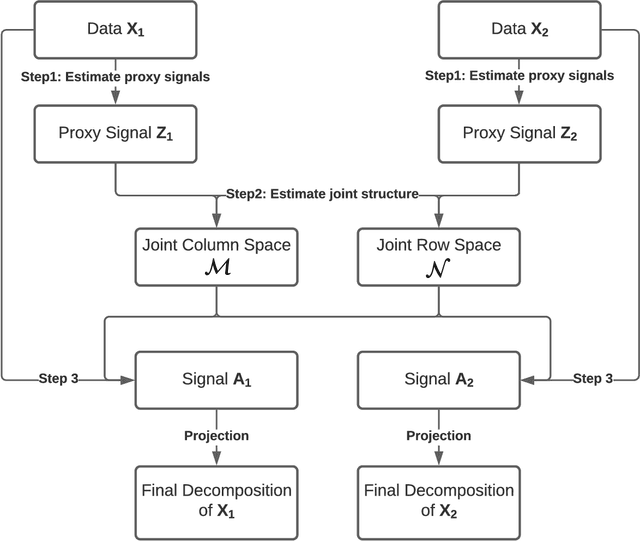
We consider the problem of extracting joint and individual signals from multi-view data, that is data collected from different sources on matched samples. While existing methods for multi-view data decomposition explore single matching of data by samples, we focus on double-matched multi-view data (matched by both samples and source features). Our motivating example is the miRNA data collected from both primary tumor and normal tissues of the same subjects; the measurements from two tissues are thus matched both by subjects and by miRNAs. Our proposed double-matched matrix decomposition allows to simultaneously extract joint and individual signals across subjects, as well as joint and individual signals across miRNAs. Our estimation approach takes advantage of double-matching by formulating a new type of optimization problem with explicit row space and column space constraints, for which we develop an efficient iterative algorithm. Numerical studies indicate that taking advantage of double-matching leads to superior signal estimation performance compared to existing multi-view data decomposition based on single-matching. We apply our method to miRNA data as well as data from the English Premier League soccer matches, and find joint and individual multi-view signals that align with domain specific knowledge.

Compressing Large Sample Data for Discriminant Analysis

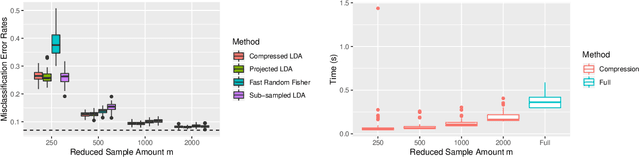
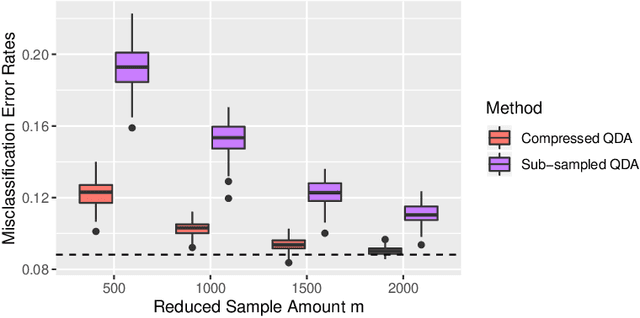
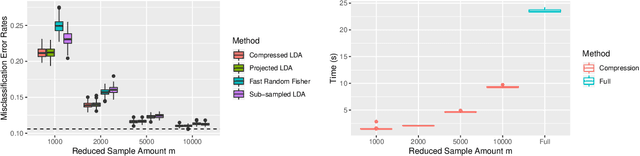
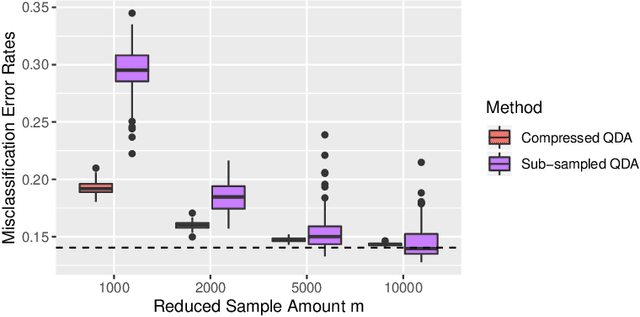
Large-sample data became prevalent as data acquisition became cheaper and easier. While a large sample size has theoretical advantages for many statistical methods, it presents computational challenges. Sketching, or compression, is a well-studied approach to address these issues in regression settings, but considerably less is known about its performance in classification settings. Here we consider the computational issues due to large sample size within the discriminant analysis framework. We propose a new compression approach for reducing the number of training samples for linear and quadratic discriminant analysis, in contrast to existing compression methods which focus on reducing the number of features. We support our approach with a theoretical bound on the misclassification error rate compared to the Bayes classifier. Empirical studies confirm the significant computational gains of the proposed method and its superior predictive ability compared to random sub-sampling.

Sparse Feature Selection in Kernel Discriminant Analysis via Optimal Scoring

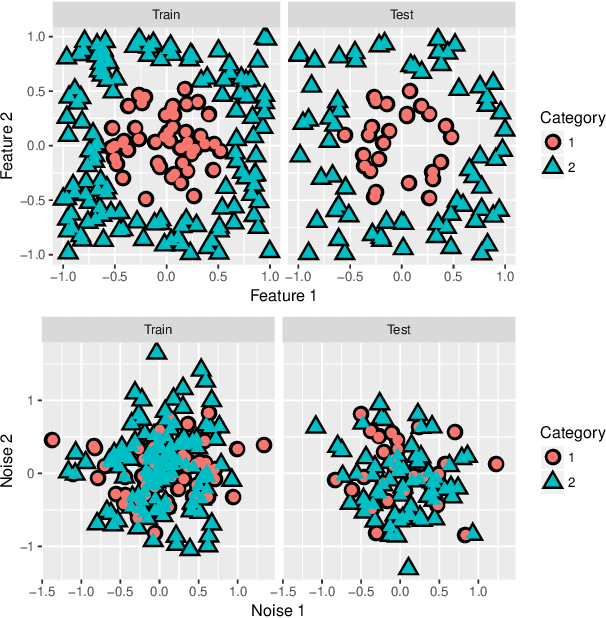
We consider the two-group classification problem and propose a kernel classifier based on the optimal scoring framework. Unlike previous approaches, we provide theoretical guarantees on the expected risk consistency of the method. We also allow for feature selection by imposing structured sparsity using weighted kernels. We propose fully-automated methods for selection of all tuning parameters, and in particular adapt kernel shrinkage ideas for ridge parameter selection. Numerical studies demonstrate the superior classification performance of the proposed approach compared to existing nonparametric classifiers.

Joint association and classification analysis of multi-view data

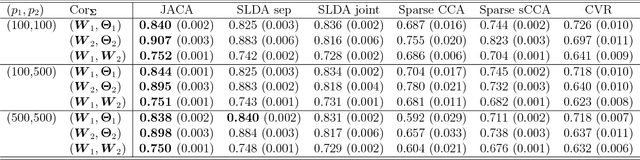
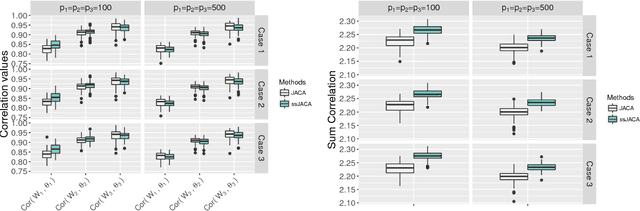
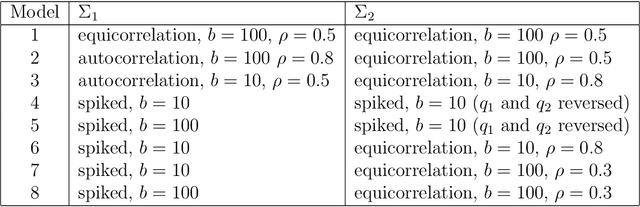
Multi-view data, that is matched sets of measurements on the same subjects, have become increasingly common with technological advances in genomics and other fields. Often, the subjects are separated into known classes, and it is of interest to find associations between the views that are related to the class membership. Existing classification methods can either be applied to each view separately, or to the concatenated matrix of all views without taking into account between-views associations. On the other hand, existing association methods can not directly incorporate class information. In this work we propose a framework for Joint Association and Classification Analysis of multi-view data (JACA). We support the methodology with theoretical guarantees for estimation consistency in high-dimensional settings, and numerical comparisons with existing methods. In addition to joint learning framework, a distinct advantage of our approach is its ability to use partial information: it can be applied both in the settings with missing class labels, and in the settings with missing subsets of views. We apply JACA to colorectal cancer data from The Cancer Genome Atlas project, and quantify the association between RNAseq and miRNA views with respect to consensus molecular subtypes of colorectal cancer.

Oracle Inequalities for High-dimensional Prediction

The abundance of high-dimensional data in the modern sciences has generated tremendous interest in penalized estimators such as the lasso, scaled lasso, square-root lasso, elastic net, and many others. In this paper, we establish a general oracle inequality for prediction in high-dimensional linear regression with such methods. Since the proof relies only on convexity and continuity arguments, the result holds irrespective of the design matrix and applies to a wide range of penalized estimators. Overall, the bound demonstrates that generic estimators can provide consistent prediction with any design matrix. From a practical point of view, the bound can help to identify the potential of specific estimators, and they can help to get a sense of the prediction accuracy in a given application.

Sparse quadratic classification rules via linear dimension reduction

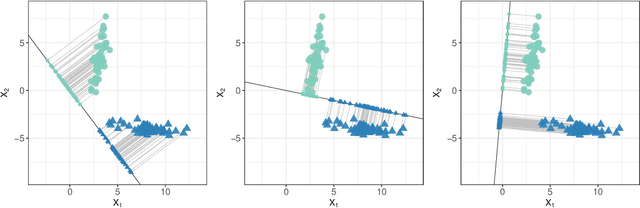
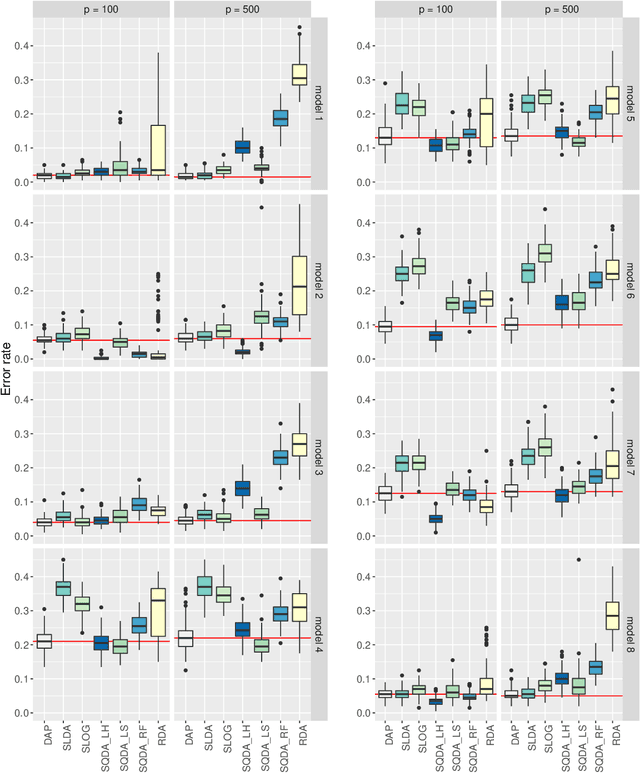
We consider the problem of high-dimensional classification between the two groups with unequal covariance matrices. Rather than estimating the full quadratic discriminant rule, we propose to perform simultaneous variable selection and linear dimension reduction on original data, with the subsequent application of quadratic discriminant analysis on the reduced space. In contrast to quadratic discriminant analysis, the proposed framework doesn't require estimation of precision matrices and scales linearly with the number of measurements, making it especially attractive for the use on high-dimensional datasets. We support the methodology with theoretical guarantees on variable selection consistency, and empirical comparison with competing approaches. We apply the method to gene expression data of breast cancer patients, and confirm the crucial importance of ESR1 gene in differentiating estrogen receptor status.