Carson James
Learning Joint and Individual Structure in Network Data with Covariates
Jun 13, 2024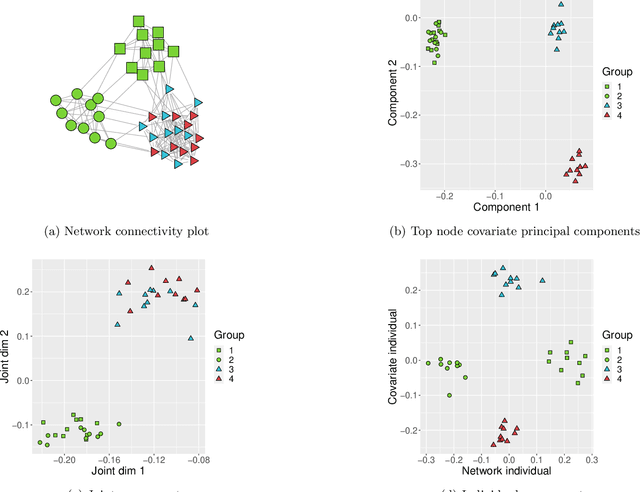

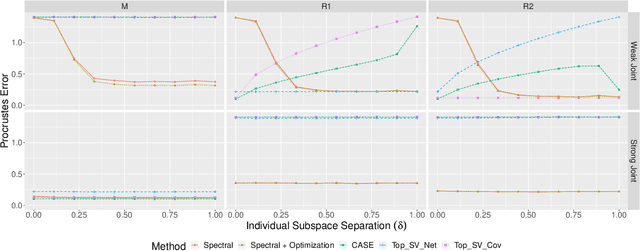
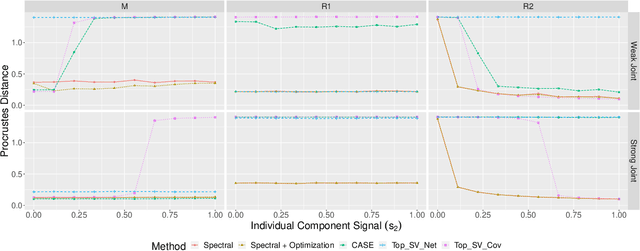
Abstract:Datasets consisting of a network and covariates associated with its vertices have become ubiquitous. One problem pertaining to this type of data is to identify information unique to the network, information unique to the vertex covariates and information that is shared between the network and the vertex covariates. Existing techniques for network data and vertex covariates focus on capturing structure that is shared but are usually not able to differentiate structure that is unique to each dataset. This work formulates a low-rank model that simultaneously captures joint and individual information in network data with vertex covariates. A two-step estimation procedure is proposed, composed of an efficient spectral method followed by a refinement optimization step. Theoretically, we show that the spectral method is able to consistently recover the joint and individual components under a general signal-plus-noise model. Simulations and real data examples demonstrate the ability of the methods to recover accurate and interpretable components. In particular, the application of the methodology to a food trade network between countries with economic, developmental and geographical country-level indicators as covariates yields joint and individual factors that explain the trading patterns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge