Learning Joint and Individual Structure in Network Data with Covariates

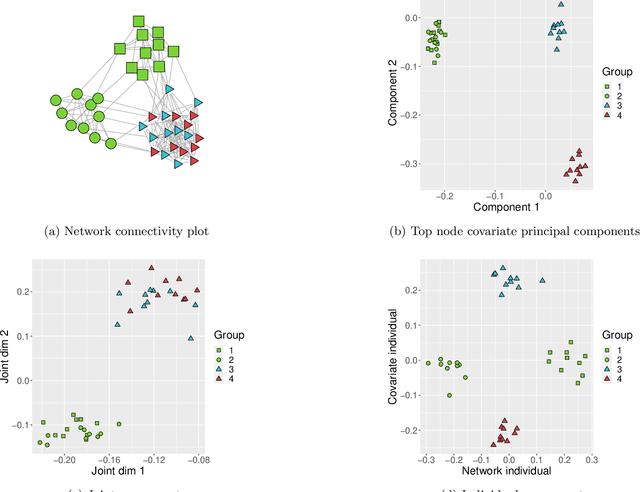
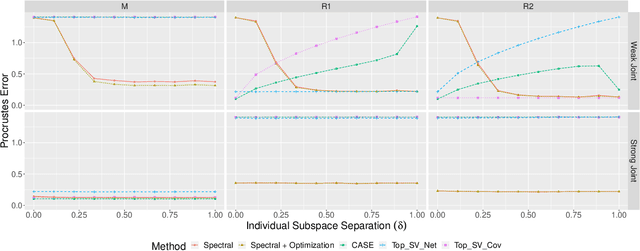
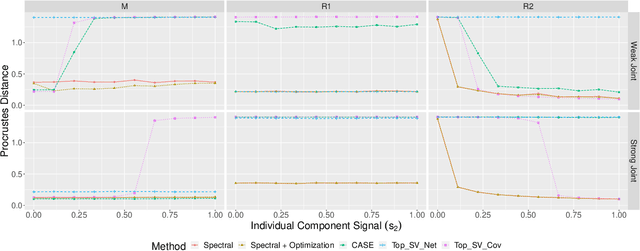
Datasets consisting of a network and covariates associated with its vertices have become ubiquitous. One problem pertaining to this type of data is to identify information unique to the network, information unique to the vertex covariates and information that is shared between the network and the vertex covariates. Existing techniques for network data and vertex covariates focus on capturing structure that is shared but are usually not able to differentiate structure that is unique to each dataset. This work formulates a low-rank model that simultaneously captures joint and individual information in network data with vertex covariates. A two-step estimation procedure is proposed, composed of an efficient spectral method followed by a refinement optimization step. Theoretically, we show that the spectral method is able to consistently recover the joint and individual components under a general signal-plus-noise model. Simulations and real data examples demonstrate the ability of the methods to recover accurate and interpretable components. In particular, the application of the methodology to a food trade network between countries with economic, developmental and geographical country-level indicators as covariates yields joint and individual factors that explain the trading patterns.

Overlapping community detection in networks via sparse spectral decomposition

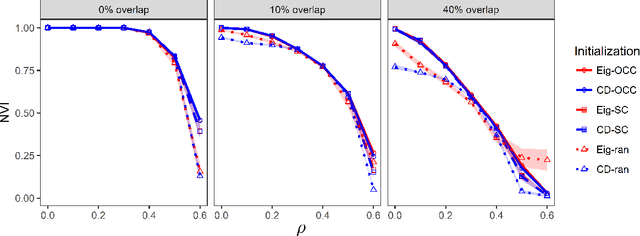
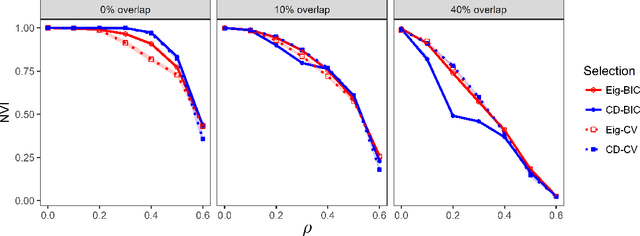
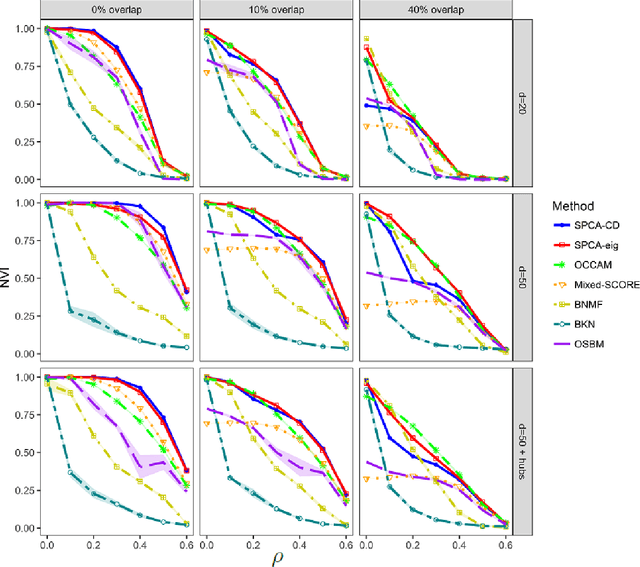
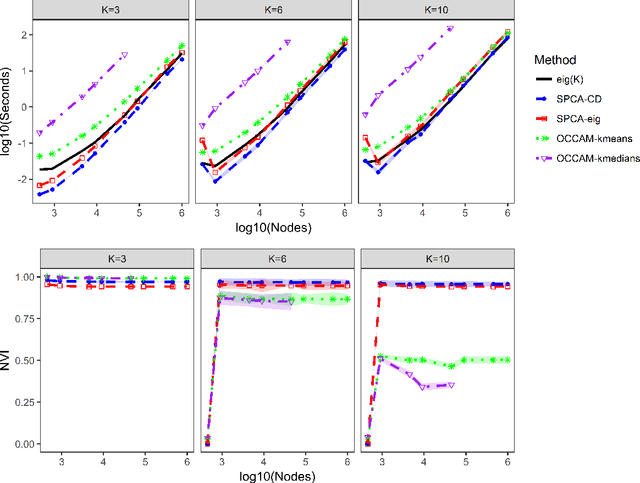
We consider the problem of estimating overlapping community memberships in a network, where each node can belong to multiple communities. More than a few communities per node are difficult to both estimate and interpret, so we focus on sparse node membership vectors. Our algorithm is based on sparse principal subspace estimation with iterative thresholding. The method is computationally efficient, with a computational cost equivalent to estimating the leading eigenvectors of the adjacency matrix, and does not require an additional clustering step, unlike spectral clustering methods. We show that a fixed point of the algorithm corresponds to correct node memberships under a version of the stochastic block model. The methods are evaluated empirically on simulated and real-world networks, showing good statistical performance and computational efficiency.

Simultaneous prediction and community detection for networks with application to neuroimaging

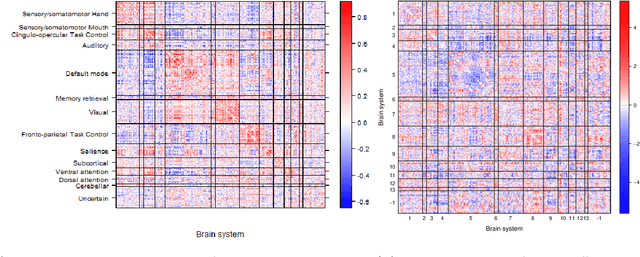
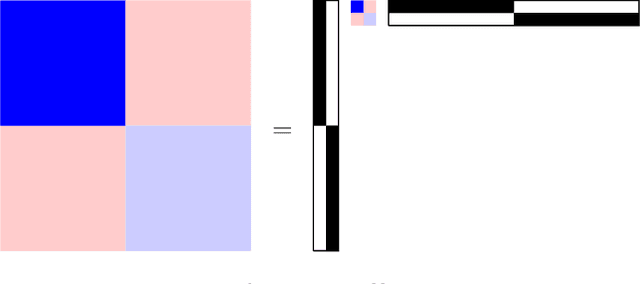
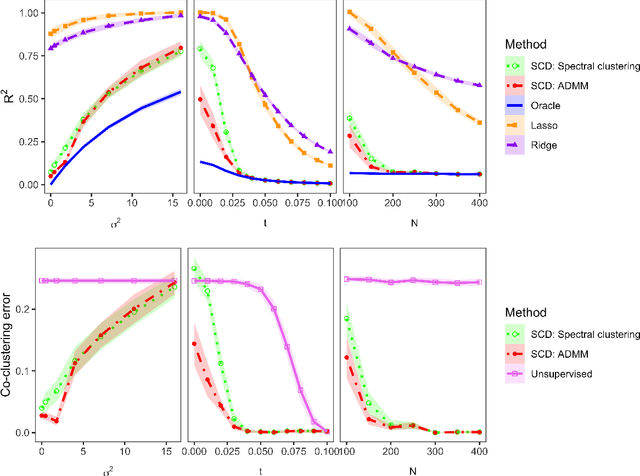
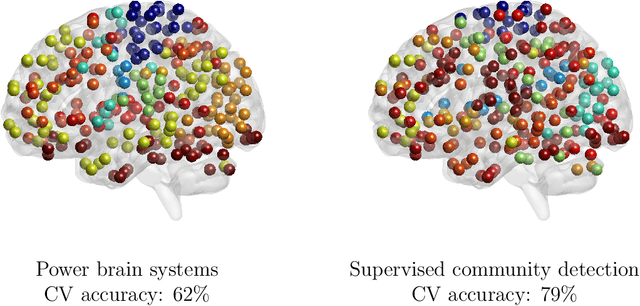
Community structure in networks is observed in many different domains, and unsupervised community detection has received a lot of attention in the literature. Increasingly the focus of network analysis is shifting towards using network information in some other prediction or inference task rather than just analyzing the network itself. In particular, in neuroimaging applications brain networks are available for multiple subjects and the goal is often to predict a phenotype of interest. Community structure is well known to be a feature of brain networks, typically corresponding to different regions of the brain responsible for different functions. There are standard parcellations of the brain into such regions, usually obtained by applying clustering methods to brain connectomes of healthy subjects. However, when the goal is predicting a phenotype or distinguishing between different conditions, these static communities from an unrelated set of healthy subjects may not be the most useful for prediction. Here we present a method for supervised community detection, aiming to find a partition of the network into communities that is most useful for predicting a particular response. We use a block-structured regularization penalty combined with a prediction loss function, and compute the solution with a combination of a spectral method and an ADMM optimization algorithm. We show that the spectral clustering method recovers the correct communities under a weighted stochastic block model. The method performs well on both simulated and real brain networks, providing support for the idea of task-dependent brain regions.

Graph matching between bipartite and unipartite networks: to collapse, or not to collapse, that is the question

Graph matching consists of aligning the vertices of two unlabeled graphs in order to maximize the shared structure across networks; when the graphs are unipartite, this is commonly formulated as minimizing their edge disagreements. In this paper, we address the common setting in which one of the graphs to match is a bipartite network and one is unipartite. Commonly, the bipartite networks are collapsed or projected into a unipartite graph, and graph matching proceeds as in the classical setting. This potentially leads to noisy edge estimates and loss of information. We formulate the graph matching problem between a bipartite and a unipartite graph using an undirected graphical model, and introduce methods to find the alignment with this model without collapsing. In simulations and real data examples, we show how our methods can result in a more accurate matching than the naive approach of transforming the bipartite networks into unipartite, and we demonstrate the performance gains achieved by our method in simulated and real data networks, including a co-authorship-citation network pair and brain structural and functional data.

Maximum Likelihood Estimation and Graph Matching in Errorfully Observed Networks

Given a pair of graphs with the same number of vertices, the inexact graph matching problem consists in finding a correspondence between the vertices of these graphs that minimizes the total number of induced edge disagreements. We study this problem from a statistical framework in which one of the graphs is an errorfully observed copy of the other. We introduce a corrupting channel model, and show that in this model framework, the solution to the graph matching problem is a maximum likelihood estimator. Necessary and sufficient conditions for consistency of this MLE are presented, as well as a relaxed notion of consistency in which a negligible fraction of the vertices need not be matched correctly. The results are used to study matchability in several families of random graphs, including edge independent models, random regular graphs and small-world networks. We also use these results to introduce measures of matching feasibility, and experimentally validate the results on simulated and real-world networks.

Efficient Distributed Estimation of Inverse Covariance Matrices

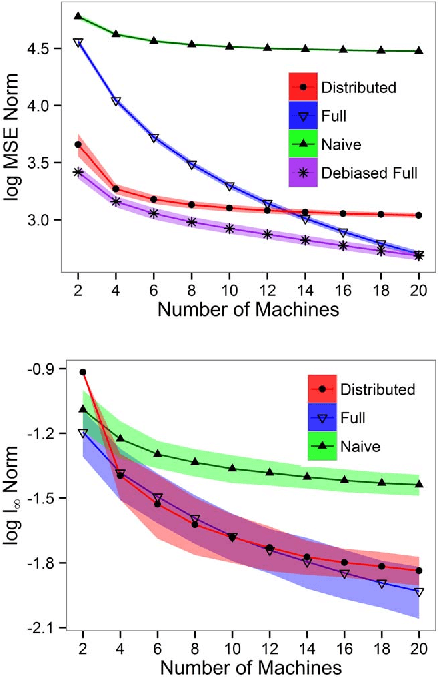
In distributed systems, communication is a major concern due to issues such as its vulnerability or efficiency. In this paper, we are interested in estimating sparse inverse covariance matrices when samples are distributed into different machines. We address communication efficiency by proposing a method where, in a single round of communication, each machine transfers a small subset of the entries of the inverse covariance matrix. We show that, with this efficient distributed method, the error rates can be comparable with estimation in a non-distributed setting, and correct model selection is still possible. Practical performance is shown through simulations.