Regularization can make diffusion models more efficient

Diffusion models are one of the key architectures of generative AI. Their main drawback, however, is the computational costs. This study indicates that the concept of sparsity, well known especially in statistics, can provide a pathway to more efficient diffusion pipelines. Our mathematical guarantees prove that sparsity can reduce the input dimension's influence on the computational complexity to that of a much smaller intrinsic dimension of the data. Our empirical findings confirm that inducing sparsity can indeed lead to better samples at a lower cost.

AnomalyDINO: Boosting Patch-based Few-shot Anomaly Detection with DINOv2

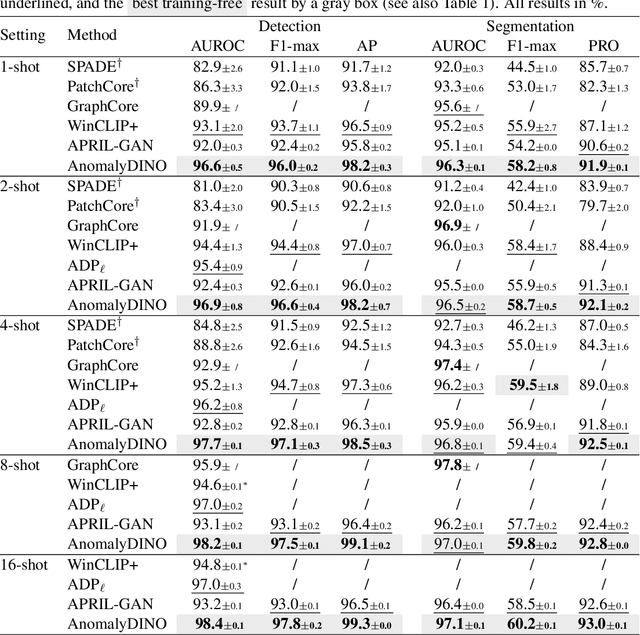
Recent advances in multimodal foundation models have set new standards in few-shot anomaly detection. This paper explores whether high-quality visual features alone are sufficient to rival existing state-of-the-art vision-language models. We affirm this by adapting DINOv2 for one-shot and few-shot anomaly detection, with a focus on industrial applications. We show that this approach does not only rival existing techniques but can even outmatch them in many settings. Our proposed vision-only approach, AnomalyDINO, is based on patch similarities and enables both image-level anomaly prediction and pixel-level anomaly segmentation. The approach is methodologically simple and training-free and, thus, does not require any additional data for fine-tuning or meta-learning. Despite its simplicity, AnomalyDINO achieves state-of-the-art results in one- and few-shot anomaly detection (e.g., pushing the one-shot performance on MVTec-AD from an AUROC of 93.1% to 96.6%). The reduced overhead, coupled with its outstanding few-shot performance, makes AnomalyDINO a strong candidate for fast deployment, for example, in industrial contexts.

Benchmarking the Fairness of Image Upsampling Methods

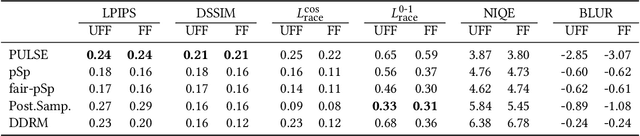
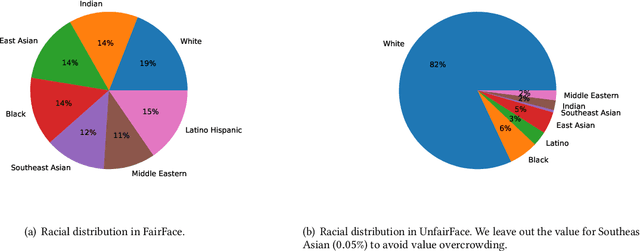
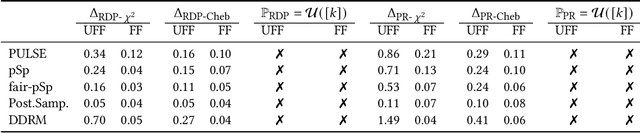
Recent years have witnessed a rapid development of deep generative models for creating synthetic media, such as images and videos. While the practical applications of these models in everyday tasks are enticing, it is crucial to assess the inherent risks regarding their fairness. In this work, we introduce a comprehensive framework for benchmarking the performance and fairness of conditional generative models. We develop a set of metrics$\unicode{x2013}$inspired by their supervised fairness counterparts$\unicode{x2013}$to evaluate the models on their fairness and diversity. Focusing on the specific application of image upsampling, we create a benchmark covering a wide variety of modern upsampling methods. As part of the benchmark, we introduce UnfairFace, a subset of FairFace that replicates the racial distribution of common large-scale face datasets. Our empirical study highlights the importance of using an unbiased training set and reveals variations in how the algorithms respond to dataset imbalances. Alarmingly, we find that none of the considered methods produces statistically fair and diverse results.

Affine Invariance in Continuous-Domain Convolutional Neural Networks

The notion of group invariance helps neural networks in recognizing patterns and features under geometric transformations. Indeed, it has been shown that group invariance can largely improve deep learning performances in practice, where such transformations are very common. This research studies affine invariance on continuous-domain convolutional neural networks. Despite other research considering isometric invariance or similarity invariance, we focus on the full structure of affine transforms generated by the generalized linear group $\mathrm{GL}_2(\mathbb{R})$. We introduce a new criterion to assess the similarity of two input signals under affine transformations. Then, unlike conventional methods that involve solving complex optimization problems on the Lie group $G_2$, we analyze the convolution of lifted signals and compute the corresponding integration over $G_2$. In sum, our research could eventually extend the scope of geometrical transformations that practical deep-learning pipelines can handle.

Single-Model Attribution via Final-Layer Inversion

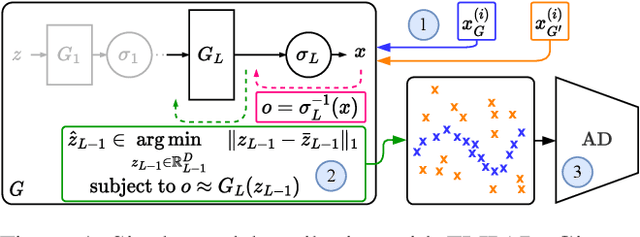
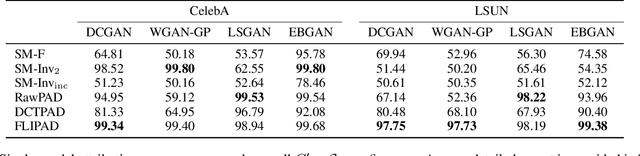
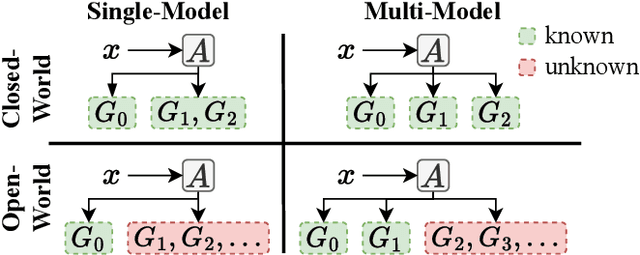
Recent groundbreaking developments on generative modeling have sparked interest in practical single-model attribution. Such methods predict whether a sample was generated by a specific generator or not, for instance, to prove intellectual property theft. However, previous works are either limited to the closed-world setting or require undesirable changes of the generative model. We address these shortcomings by proposing FLIPAD, a new approach for single-model attribution in the open-world setting based on final-layer inversion and anomaly detection. We show that the utilized final-layer inversion can be reduced to a convex lasso optimization problem, making our approach theoretically sound and computationally efficient. The theoretical findings are accompanied by an experimental study demonstrating the effectiveness of our approach, outperforming the existing methods.

Lag selection and estimation of stable parameters for multiple autoregressive processes through convex programming

Motivated by a variety of applications, high-dimensional time series have become an active topic of research. In particular, several methods and finite-sample theories for individual stable autoregressive processes with known lag have become available very recently. We, instead, consider multiple stable autoregressive processes that share an unknown lag. We use information across the different processes to simultaneously select the lag and estimate the parameters. We prove that the estimated process is stable, and we establish rates for the forecasting error that can outmatch the known rate in our setting. Our insights on the lag selection and the stability are also of interest for the case of individual autoregressive processes.

The DeepCAR Method: Forecasting Time-Series Data That Have Change Points

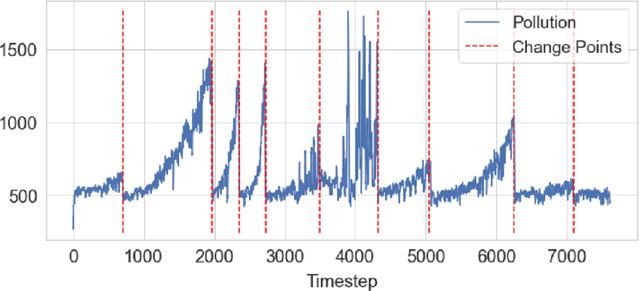
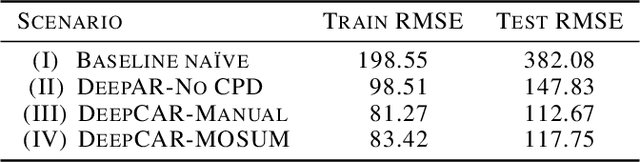
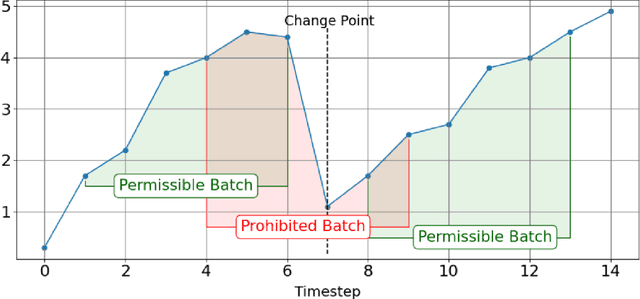
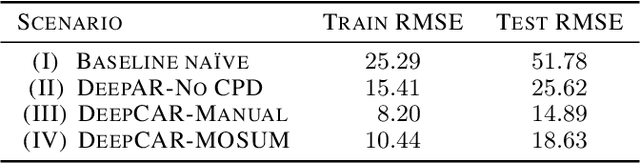
Many methods for time-series forecasting are known in classical statistics, such as autoregression, moving averages, and exponential smoothing. The DeepAR framework is a novel, recent approach for time-series forecasting based on deep learning. DeepAR has shown very promising results already. However, time series often have change points, which can degrade the DeepAR's prediction performance substantially. This paper extends the DeepAR framework by detecting and including those change points. We show that our method performs as well as standard DeepAR when there are no change points and considerably better when there are change points. More generally, we show that the batch size provides an effective and surprisingly simple way to deal with change points in DeepAR, Transformers, and other modern forecasting models.

Statistical guarantees for sparse deep learning

Neural networks are becoming increasingly popular in applications, but our mathematical understanding of their potential and limitations is still limited. In this paper, we further this understanding by developing statistical guarantees for sparse deep learning. In contrast to previous work, we consider different types of sparsity, such as few active connections, few active nodes, and other norm-based types of sparsity. Moreover, our theories cover important aspects that previous theories have neglected, such as multiple outputs, regularization, and l2-loss. The guarantees have a mild dependence on network widths and depths, which means that they support the application of sparse but wide and deep networks from a statistical perspective. Some of the concepts and tools that we use in our derivations are uncommon in deep learning and, hence, might be of additional interest.

Marginal Tail-Adaptive Normalizing Flows

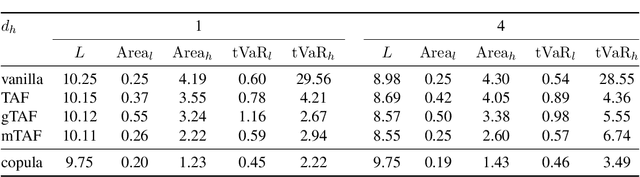
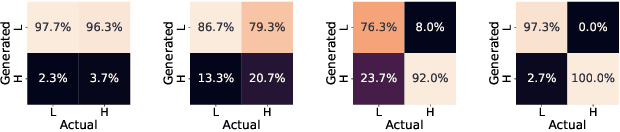
Learning the tail behavior of a distribution is a notoriously difficult problem. By definition, the number of samples from the tail is small, and deep generative models, such as normalizing flows, tend to concentrate on learning the body of the distribution. In this paper, we focus on improving the ability of normalizing flows to correctly capture the tail behavior and, thus, form more accurate models. We prove that the marginal tailedness of an autoregressive flow can be controlled via the tailedness of the marginals of its base distribution. This theoretical insight leads us to a novel type of flows based on flexible base distributions and data-driven linear layers. An empirical analysis shows that the proposed method improves on the accuracy -- especially on the tails of the distribution -- and is able to generate heavy-tailed data. We demonstrate its application on a weather and climate example, in which capturing the tail behavior is essential.

Statistical Guarantees for Approximate Stationary Points of Simple Neural Networks

Since statistical guarantees for neural networks are usually restricted to global optima of intricate objective functions, it is not clear whether these theories really explain the performances of actual outputs of neural-network pipelines. The goal of this paper is, therefore, to bring statistical theory closer to practice. We develop statistical guarantees for simple neural networks that coincide up to logarithmic factors with the global optima but apply to stationary points and the points nearby. These results support the common notion that neural networks do not necessarily need to be optimized globally from a mathematical perspective. More generally, despite being limited to simple neural networks for now, our theories make a step forward in describing the practical properties of neural networks in mathematical terms.