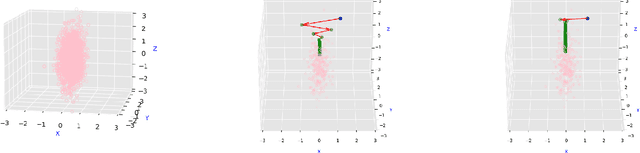
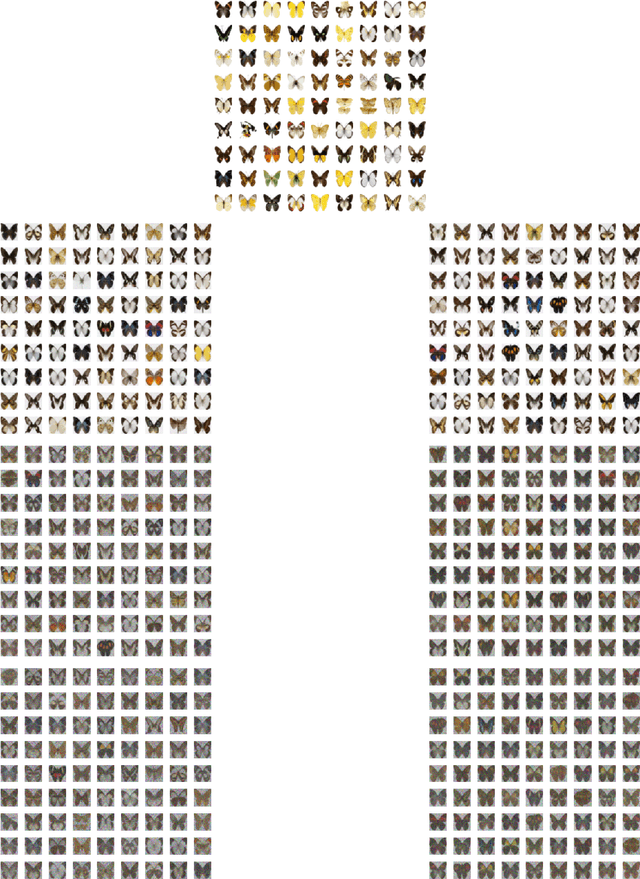
Regularization can make diffusion models more efficient

Diffusion models are one of the key architectures of generative AI. Their main drawback, however, is the computational costs. This study indicates that the concept of sparsity, well known especially in statistics, can provide a pathway to more efficient diffusion pipelines. Our mathematical guarantees prove that sparsity can reduce the input dimension's influence on the computational complexity to that of a much smaller intrinsic dimension of the data. Our empirical findings confirm that inducing sparsity can indeed lead to better samples at a lower cost.

Statistical Guarantees for Approximate Stationary Points of Simple Neural Networks

Since statistical guarantees for neural networks are usually restricted to global optima of intricate objective functions, it is not clear whether these theories really explain the performances of actual outputs of neural-network pipelines. The goal of this paper is, therefore, to bring statistical theory closer to practice. We develop statistical guarantees for simple neural networks that coincide up to logarithmic factors with the global optima but apply to stationary points and the points nearby. These results support the common notion that neural networks do not necessarily need to be optimized globally from a mathematical perspective. More generally, despite being limited to simple neural networks for now, our theories make a step forward in describing the practical properties of neural networks in mathematical terms.

Statistical Guarantees for Regularized Neural Networks

Neural networks have become standard tools in the analysis of data, but they lack comprehensive mathematical theories. For example, there are very few statistical guarantees for learning neural networks from data, especially for classes of estimators that are used in practice or at least similar to such. In this paper, we develop a general statistical guarantee for estimators that consist of a least-squares term and a regularizer. We then exemplify this guarantee with $\ell_1$-regularization, showing that the corresponding prediction error increases at most sub-linearly in the number of layers and at most logarithmically in the total number of parameters. Our results establish a mathematical basis for regularized estimation of neural networks, and they deepen our mathematical understanding of neural networks and deep learning more generally.