Compressing Large Sample Data for Discriminant Analysis

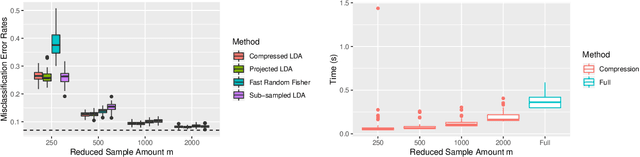
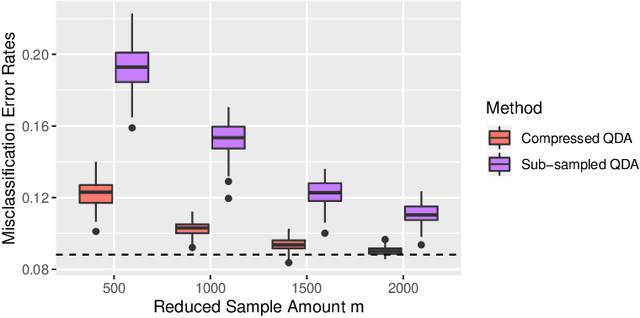
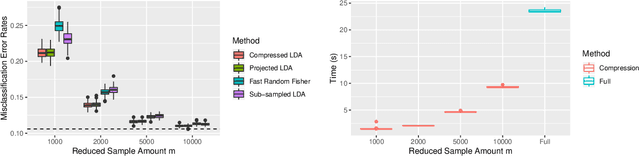
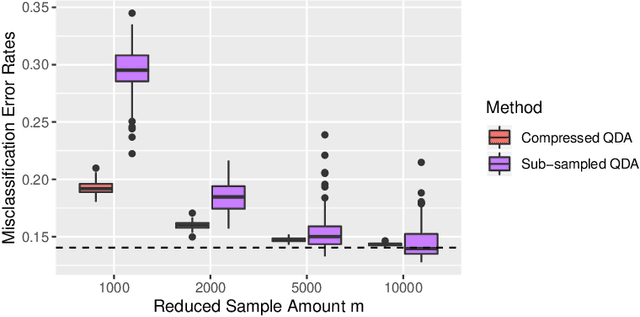
Large-sample data became prevalent as data acquisition became cheaper and easier. While a large sample size has theoretical advantages for many statistical methods, it presents computational challenges. Sketching, or compression, is a well-studied approach to address these issues in regression settings, but considerably less is known about its performance in classification settings. Here we consider the computational issues due to large sample size within the discriminant analysis framework. We propose a new compression approach for reducing the number of training samples for linear and quadratic discriminant analysis, in contrast to existing compression methods which focus on reducing the number of features. We support our approach with a theoretical bound on the misclassification error rate compared to the Bayes classifier. Empirical studies confirm the significant computational gains of the proposed method and its superior predictive ability compared to random sub-sampling.