Progression: an extrapolation principle for regression

The problem of regression extrapolation, or out-of-distribution generalization, arises when predictions are required at test points outside the range of the training data. In such cases, the non-parametric guarantees for regression methods from both statistics and machine learning typically fail. Based on the theory of tail dependence, we propose a novel statistical extrapolation principle. After a suitable, data-adaptive marginal transformation, it assumes a simple relationship between predictors and the response at the boundary of the training predictor samples. This assumption holds for a wide range of models, including non-parametric regression functions with additive noise. Our semi-parametric method, progression, leverages this extrapolation principle and offers guarantees on the approximation error beyond the training data range. We demonstrate how this principle can be effectively integrated with existing approaches, such as random forests and additive models, to improve extrapolation performance on out-of-distribution samples.

Validating Deep-Learning Weather Forecast Models on Recent High-Impact Extreme Events

The forecast accuracy of deep-learning-based weather prediction models is improving rapidly, leading many to speak of a "second revolution in weather forecasting". With numerous methods being developed, and limited physical guarantees offered by deep-learning models, there is a critical need for comprehensive evaluation of these emerging techniques. While this need has been partly fulfilled by benchmark datasets, they provide little information on rare and impactful extreme events, or on compound impact metrics, for which model accuracy might degrade due to misrepresented dependencies between variables. To address these issues, we compare deep-learning weather prediction models (GraphCast, PanguWeather, FourCastNet) and ECMWF's high-resolution forecast (HRES) system in three case studies: the 2021 Pacific Northwest heatwave, the 2023 South Asian humid heatwave, and the North American winter storm in 2021. We find evidence that machine learning (ML) weather prediction models can locally achieve similar accuracy to HRES on record-shattering events such as the 2021 Pacific Northwest heatwave and even forecast the compound 2021 North American winter storm substantially better. However, extrapolating to extreme conditions may impact machine learning models more severely than HRES, as evidenced by the comparable or superior spatially- and temporally-aggregated forecast accuracy of HRES for the two heatwaves studied. The ML forecasts also lack variables required to assess the health risks of events such as the 2023 South Asian humid heatwave. Generally, case-study-driven, impact-centric evaluation can complement existing research, increase public trust, and aid in developing reliable ML weather prediction models.

Extremal graphical modeling with latent variables

Extremal graphical models encode the conditional independence structure of multivariate extremes and provide a powerful tool for quantifying the risk of rare events. Prior work on learning these graphs from data has focused on the setting where all relevant variables are observed. For the popular class of H\"usler-Reiss models, we propose the \texttt{eglatent} method, a tractable convex program for learning extremal graphical models in the presence of latent variables. Our approach decomposes the H\"usler-Reiss precision matrix into a sparse component encoding the graphical structure among the observed variables after conditioning on the latent variables, and a low-rank component encoding the effect of a few latent variables on the observed variables. We provide finite-sample guarantees of \texttt{eglatent} and show that it consistently recovers the conditional graph as well as the number of latent variables. We highlight the improved performances of our approach on synthetic and real data.

Boosted Control Functions

Modern machine learning methods and the availability of large-scale data opened the door to accurately predict target quantities from large sets of covariates. However, existing prediction methods can perform poorly when the training and testing data are different, especially in the presence of hidden confounding. While hidden confounding is well studied for causal effect estimation (e.g., instrumental variables), this is not the case for prediction tasks. This work aims to bridge this gap by addressing predictions under different training and testing distributions in the presence of unobserved confounding. In particular, we establish a novel connection between the field of distribution generalization from machine learning, and simultaneous equation models and control function from econometrics. Central to our contribution are simultaneous equation models for distribution generalization (SIMDGs) which describe the data-generating process under a set of distributional shifts. Within this framework, we propose a strong notion of invariance for a predictive model and compare it with existing (weaker) versions. Building on the control function approach from instrumental variable regression, we propose the boosted control function (BCF) as a target of inference and prove its ability to successfully predict even in intervened versions of the underlying SIMDG. We provide necessary and sufficient conditions for identifying the BCF and show that it is worst-case optimal. We introduce the ControlTwicing algorithm to estimate the BCF and analyze its predictive performance on simulated and real world data.

Neural Networks for Extreme Quantile Regression with an Application to Forecasting of Flood Risk

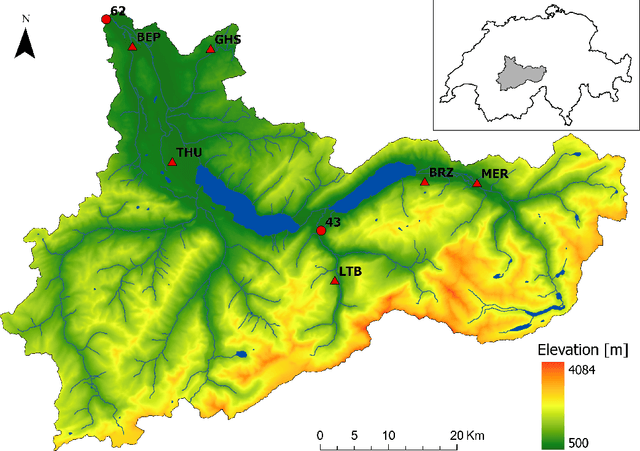
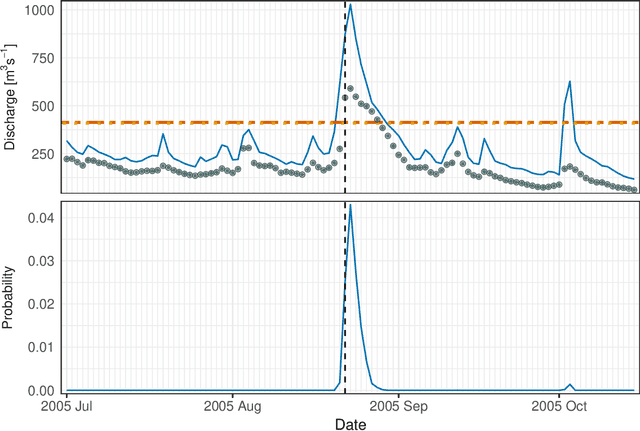
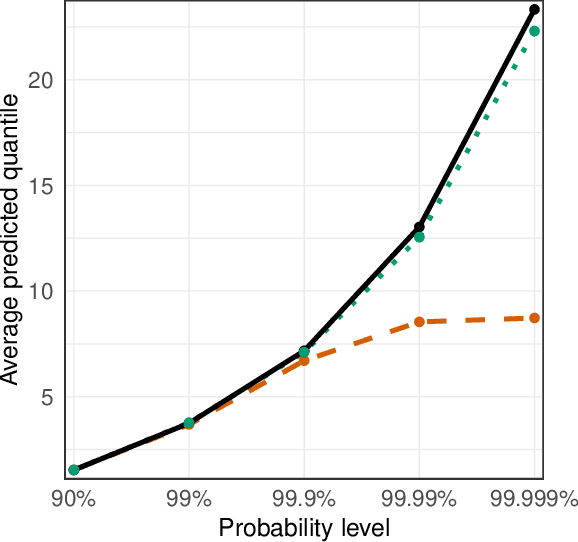
Risk assessment for extreme events requires accurate estimation of high quantiles that go beyond the range of historical observations. When the risk depends on the values of observed predictors, regression techniques are used to interpolate in the predictor space. We propose the EQRN model that combines tools from neural networks and extreme value theory into a method capable of extrapolation in the presence of complex predictor dependence. Neural networks can naturally incorporate additional structure in the data. We develop a recurrent version of EQRN that is able to capture complex sequential dependence in time series. We apply this method to forecasting of flood risk in the Swiss Aare catchment. It exploits information from multiple covariates in space and time to provide one-day-ahead predictions of return levels and exceedances probabilities. This output complements the static return level from a traditional extreme value analysis and the predictions are able to adapt to distributional shifts as experienced in a changing climate. Our model can help authorities to manage flooding more effectively and to minimize their disastrous impacts through early warning systems.

Modelling and simulating spatial extremes by combining extreme value theory with generative adversarial networks

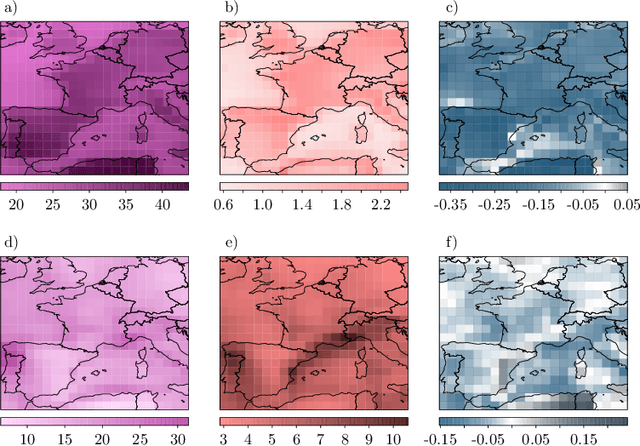
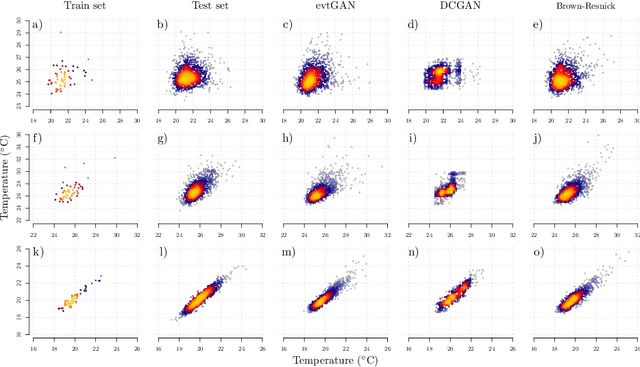
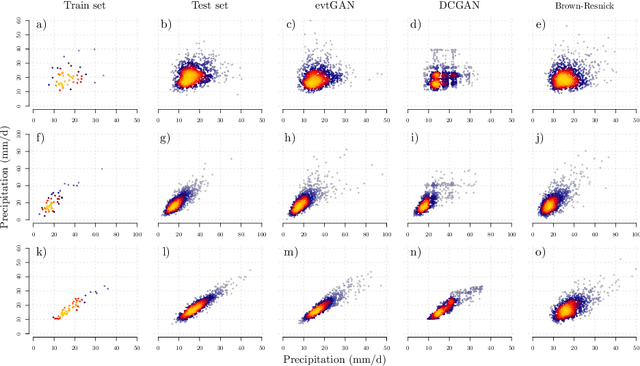
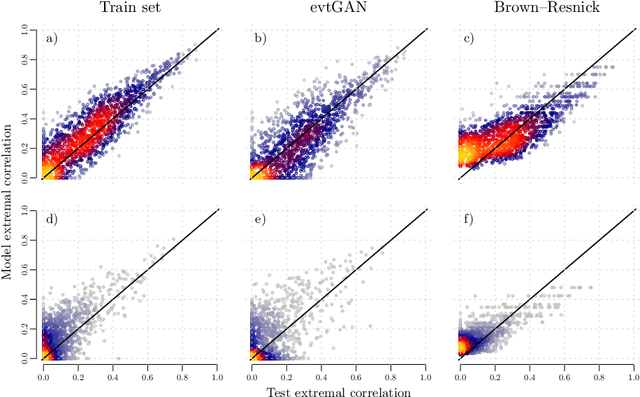
Modelling dependencies between climate extremes is important for climate risk assessment, for instance when allocating emergency management funds. In statistics, multivariate extreme value theory is often used to model spatial extremes. However, most commonly used approaches require strong assumptions and are either too simplistic or over-parametrised. From a machine learning perspective, Generative Adversarial Networks (GANs) are a powerful tool to model dependencies in high-dimensional spaces. Yet in the standard setting, GANs do not well represent dependencies in the extremes. Here we combine GANs with extreme value theory (evtGAN) to model spatial dependencies in summer maxima of temperature and winter maxima in precipitation over a large part of western Europe. We use data from a stationary 2000-year climate model simulation to validate the approach and explore its sensitivity to small sample sizes. Our results show that evtGAN outperforms classical GANs and standard statistical approaches to model spatial extremes. Already with about 50 years of data, which corresponds to commonly available climate records, we obtain reasonably good performance. In general, dependencies between temperature extremes are better captured than dependencies between precipitation extremes due to the high spatial coherence in temperature fields. Our approach can be applied to other climate variables and can be used to emulate climate models when running very long simulations to determine dependencies in the extremes is deemed infeasible.

Synergy Effect between Convolutional Neural Networks and the Multiplicity of SMILES for Improvement of Molecular Prediction

In our study, we demonstrate the synergy effect between convolutional neural networks and the multiplicity of SMILES. The model we propose, the so-called Convolutional Neural Fingerprint (CNF) model, reaches the accuracy of traditional descriptors such as Dragon (Mauri et al. [22]), RDKit (Landrum [18]), CDK2 (Willighagen et al. [43]) and PyDescriptor (Masand and Rastija [20]). Moreover the CNF model generally performs better than highly fine-tuned traditional descriptors, especially on small data sets, which is of great interest for the chemical field where data sets are generally small due to experimental costs, the availability of molecules or accessibility to private databases. We evaluate the CNF model along with SMILES augmentation during both training and testing. To the best of our knowledge, this is the first time that such a methodology is presented. We show that using the multiplicity of SMILES during training acts as a regulariser and therefore avoids overfitting and can be seen as ensemble learning when considered for testing.

Extreme Value Theory for Open Set Classification - GPD and GEV Classifiers

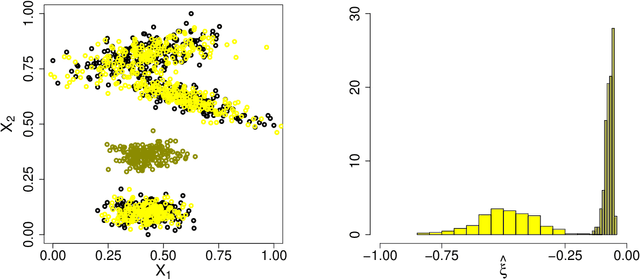
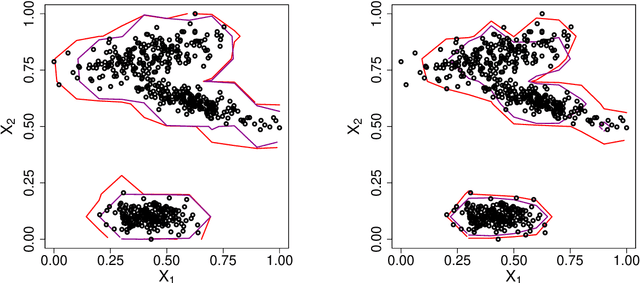
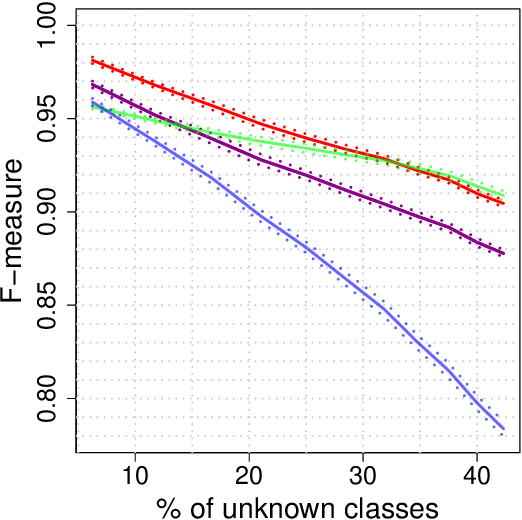
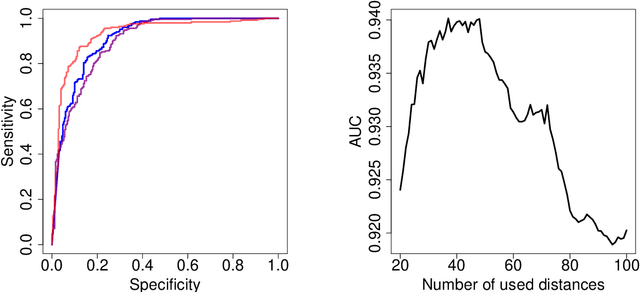
Classification tasks usually assume that all possible classes are present during the training phase. This is restrictive if the algorithm is used over a long time and possibly encounters samples from unknown classes. The recently introduced extreme value machine, a classifier motivated by extreme value theory, addresses this problem and achieves competitive performance in specific cases. We show that this algorithm can fail when the geometries of known and unknown classes differ. To overcome this problem, we propose two new algorithms relying on approximations from extreme value theory. We show the effectiveness of our classifiers in simulations and on the LETTER and MNIST data sets.