Modelling and simulating spatial extremes by combining extreme value theory with generative adversarial networks

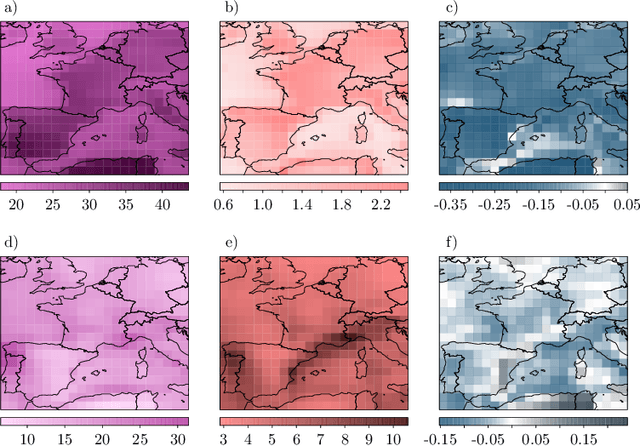
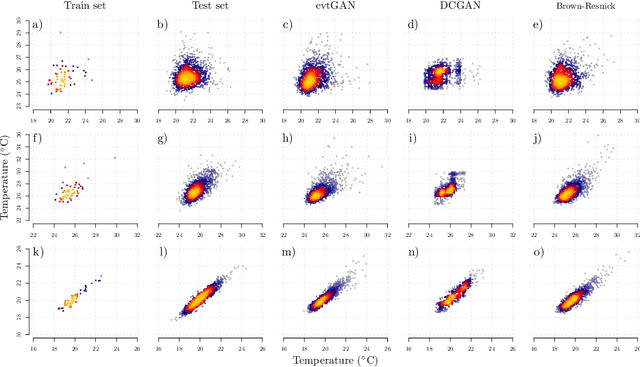
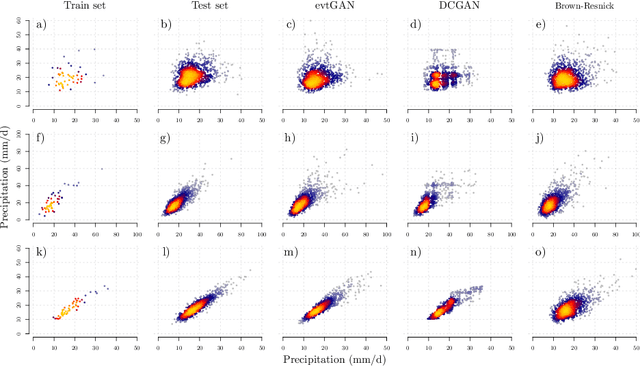
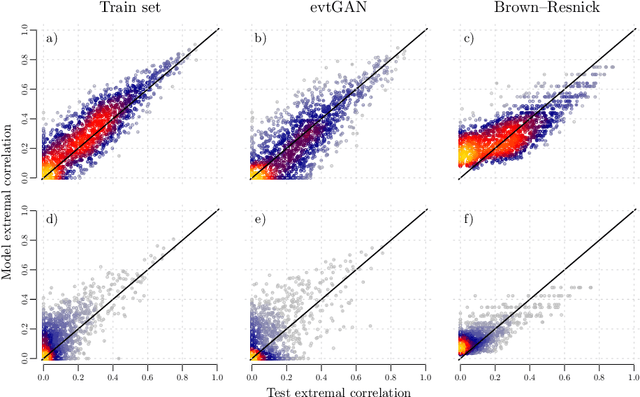
Modelling dependencies between climate extremes is important for climate risk assessment, for instance when allocating emergency management funds. In statistics, multivariate extreme value theory is often used to model spatial extremes. However, most commonly used approaches require strong assumptions and are either too simplistic or over-parametrised. From a machine learning perspective, Generative Adversarial Networks (GANs) are a powerful tool to model dependencies in high-dimensional spaces. Yet in the standard setting, GANs do not well represent dependencies in the extremes. Here we combine GANs with extreme value theory (evtGAN) to model spatial dependencies in summer maxima of temperature and winter maxima in precipitation over a large part of western Europe. We use data from a stationary 2000-year climate model simulation to validate the approach and explore its sensitivity to small sample sizes. Our results show that evtGAN outperforms classical GANs and standard statistical approaches to model spatial extremes. Already with about 50 years of data, which corresponds to commonly available climate records, we obtain reasonably good performance. In general, dependencies between temperature extremes are better captured than dependencies between precipitation extremes due to the high spatial coherence in temperature fields. Our approach can be applied to other climate variables and can be used to emulate climate models when running very long simulations to determine dependencies in the extremes is deemed infeasible.

Extreme Value Theory for Open Set Classification - GPD and GEV Classifiers

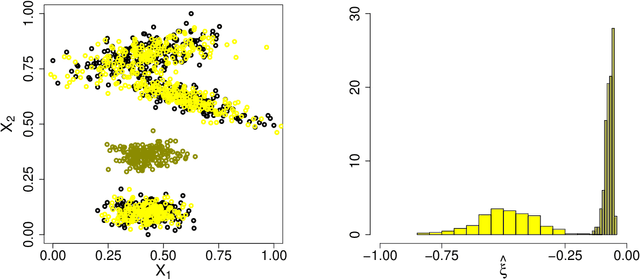
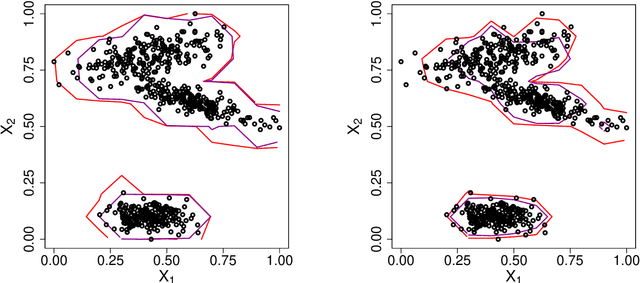
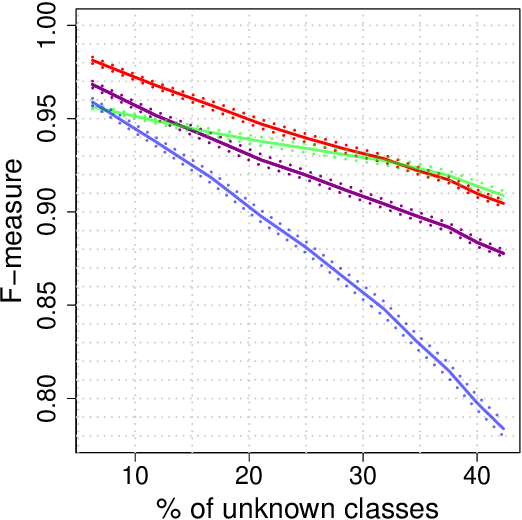
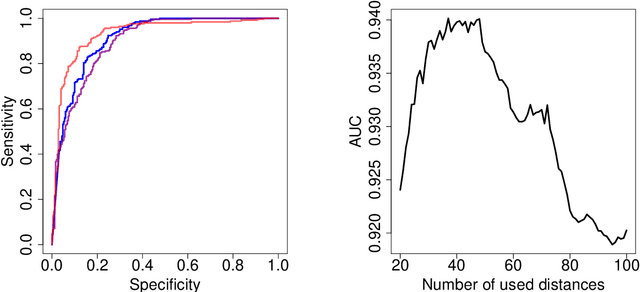
Classification tasks usually assume that all possible classes are present during the training phase. This is restrictive if the algorithm is used over a long time and possibly encounters samples from unknown classes. The recently introduced extreme value machine, a classifier motivated by extreme value theory, addresses this problem and achieves competitive performance in specific cases. We show that this algorithm can fail when the geometries of known and unknown classes differ. To overcome this problem, we propose two new algorithms relying on approximations from extreme value theory. We show the effectiveness of our classifiers in simulations and on the LETTER and MNIST data sets.