Bandits for Online Calibration: An Application to Content Moderation on Social Media Platforms

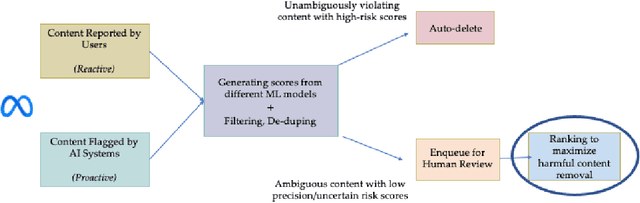
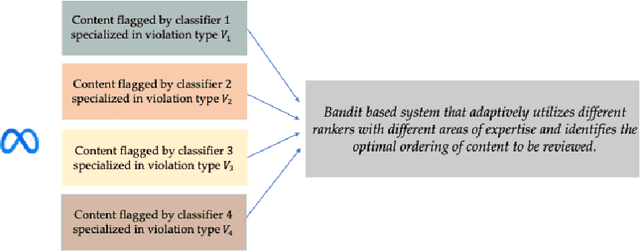
We describe the current content moderation strategy employed by Meta to remove policy-violating content from its platforms. Meta relies on both handcrafted and learned risk models to flag potentially violating content for human review. Our approach aggregates these risk models into a single ranking score, calibrating them to prioritize more reliable risk models. A key challenge is that violation trends change over time, affecting which risk models are most reliable. Our system additionally handles production challenges such as changing risk models and novel risk models. We use a contextual bandit to update the calibration in response to such trends. Our approach increases Meta's top-line metric for measuring the effectiveness of its content moderation strategy by 13%.

QUEST: Queue Simulation for Content Moderation at Scale

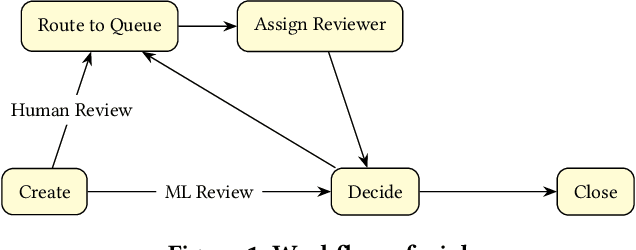
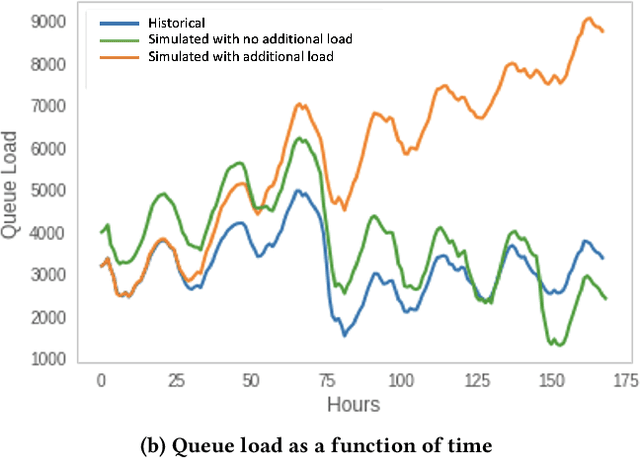
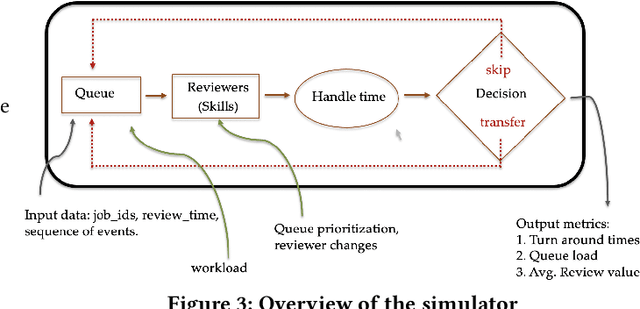
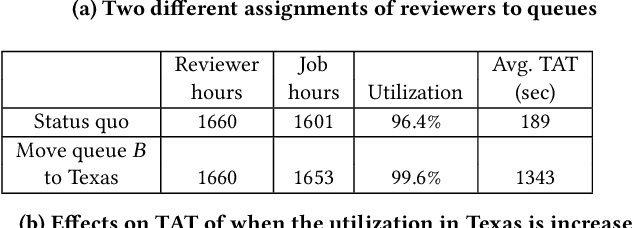
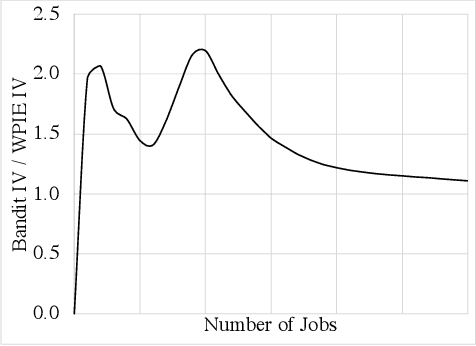
Moderating content in social media platforms is a formidable challenge due to the unprecedented scale of such systems, which typically handle billions of posts per day. Some of the largest platforms such as Facebook blend machine learning with manual review of platform content by thousands of reviewers. Operating a large-scale human review system poses interesting and challenging methodological questions that can be addressed with operations research techniques. We investigate the problem of optimally operating such a review system at scale using ideas from queueing theory and simulation.

Learning Exponential Family Graphical Models with Latent Variables using Regularized Conditional Likelihood

Fitting a graphical model to a collection of random variables given sample observations is a challenging task if the observed variables are influenced by latent variables, which can induce significant confounding statistical dependencies among the observed variables. We present a new convex relaxation framework based on regularized conditional likelihood for latent-variable graphical modeling in which the conditional distribution of the observed variables conditioned on the latent variables is given by an exponential family graphical model. In comparison to previously proposed tractable methods that proceed by characterizing the marginal distribution of the observed variables, our approach is applicable in a broader range of settings as it does not require knowledge about the specific form of distribution of the latent variables and it can be specialized to yield tractable approaches to problems in which the observed data are not well-modeled as Gaussian. We demonstrate the utility and flexibility of our framework via a series of numerical experiments on synthetic as well as real data.

Forward - Backward Greedy Algorithms for Atomic Norm Regularization

In many signal processing applications, the aim is to reconstruct a signal that has a simple representation with respect to a certain basis or frame. Fundamental elements of the basis known as "atoms" allow us to define "atomic norms" that can be used to formulate convex regularizations for the reconstruction problem. Efficient algorithms are available to solve these formulations in certain special cases, but an approach that works well for general atomic norms, both in terms of speed and reconstruction accuracy, remains to be found. This paper describes an optimization algorithm called CoGEnT that produces solutions with succinct atomic representations for reconstruction problems, generally formulated with atomic-norm constraints. CoGEnT combines a greedy selection scheme based on the conditional gradient approach with a backward (or "truncation") step that exploits the quadratic nature of the objective to reduce the basis size. We establish convergence properties and validate the algorithm via extensive numerical experiments on a suite of signal processing applications. Our algorithm and analysis also allow for inexact forward steps and for occasional enhancements of the current representation to be performed. CoGEnT can outperform the basic conditional gradient method, and indeed many methods that are tailored to specific applications, when the enhancement and truncation steps are defined appropriately. We also introduce several novel applications that are enabled by the atomic-norm framework, including tensor completion, moment problems in signal processing, and graph deconvolution.

Optimal Low-Rank Tensor Recovery from Separable Measurements: Four Contractions Suffice

Tensors play a central role in many modern machine learning and signal processing applications. In such applications, the target tensor is usually of low rank, i.e., can be expressed as a sum of a small number of rank one tensors. This motivates us to consider the problem of low rank tensor recovery from a class of linear measurements called separable measurements. As specific examples, we focus on two distinct types of separable measurement mechanisms (a) Random projections, where each measurement corresponds to an inner product of the tensor with a suitable random tensor, and (b) the completion problem where measurements constitute revelation of a random set of entries. We present a computationally efficient algorithm, with rigorous and order-optimal sample complexity results (upto logarithmic factors) for tensor recovery. Our method is based on reduction to matrix completion sub-problems and adaptation of Leurgans' method for tensor decomposition. We extend the methodology and sample complexity results to higher order tensors, and experimentally validate our theoretical results.