Online Learning with Sublinear Best-Action Queries

In online learning, a decision maker repeatedly selects one of a set of actions, with the goal of minimizing the overall loss incurred. Following the recent line of research on algorithms endowed with additional predictive features, we revisit this problem by allowing the decision maker to acquire additional information on the actions to be selected. In particular, we study the power of \emph{best-action queries}, which reveal beforehand the identity of the best action at a given time step. In practice, predictive features may be expensive, so we allow the decision maker to issue at most $k$ such queries. We establish tight bounds on the performance any algorithm can achieve when given access to $k$ best-action queries for different types of feedback models. In particular, we prove that in the full feedback model, $k$ queries are enough to achieve an optimal regret of $\Theta\left(\min\left\{\sqrt T, \frac Tk\right\}\right)$. This finding highlights the significant multiplicative advantage in the regret rate achievable with even a modest (sublinear) number $k \in \Omega(\sqrt{T})$ of queries. Additionally, we study the challenging setting in which the only available feedback is obtained during the time steps corresponding to the $k$ best-action queries. There, we provide a tight regret rate of $\Theta\left(\min\left\{\frac{T}{\sqrt k},\frac{T^2}{k^2}\right\}\right)$, which improves over the standard $\Theta\left(\frac{T}{\sqrt k}\right)$ regret rate for label efficient prediction for $k \in \Omega(T^{2/3})$.

On the convergence of loss and uncertainty-based active learning algorithms

We study convergence rates of loss and uncertainty-based active learning algorithms under various assumptions. First, we provide a set of conditions under which a convergence rate guarantee holds, and use this for linear classifiers and linearly separable datasets to show convergence rate guarantees for loss-based sampling and different loss functions. Second, we provide a framework that allows us to derive convergence rate bounds for loss-based sampling by deploying known convergence rate bounds for stochastic gradient descent algorithms. Third, and last, we propose an active learning algorithm that combines sampling of points and stochastic Polyak's step size. We show a condition on the sampling that ensures a convergence rate guarantee for this algorithm for smooth convex loss functions. Our numerical results demonstrate efficiency of our proposed algorithm.

Bandits for Online Calibration: An Application to Content Moderation on Social Media Platforms

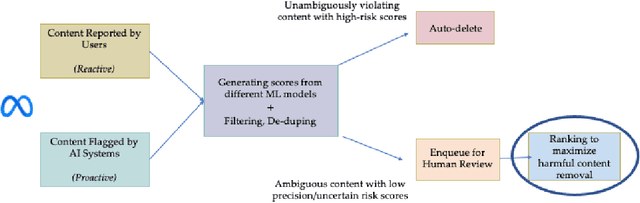
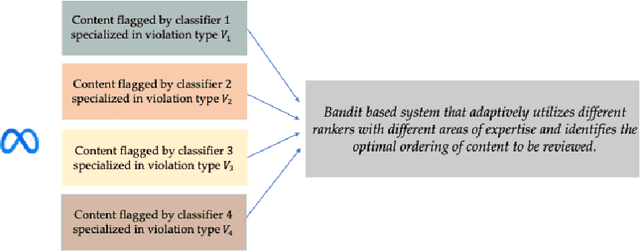
We describe the current content moderation strategy employed by Meta to remove policy-violating content from its platforms. Meta relies on both handcrafted and learned risk models to flag potentially violating content for human review. Our approach aggregates these risk models into a single ranking score, calibrating them to prioritize more reliable risk models. A key challenge is that violation trends change over time, affecting which risk models are most reliable. Our system additionally handles production challenges such as changing risk models and novel risk models. We use a contextual bandit to update the calibration in response to such trends. Our approach increases Meta's top-line metric for measuring the effectiveness of its content moderation strategy by 13%.

CUT: Controllable Unsupervised Text Simplification

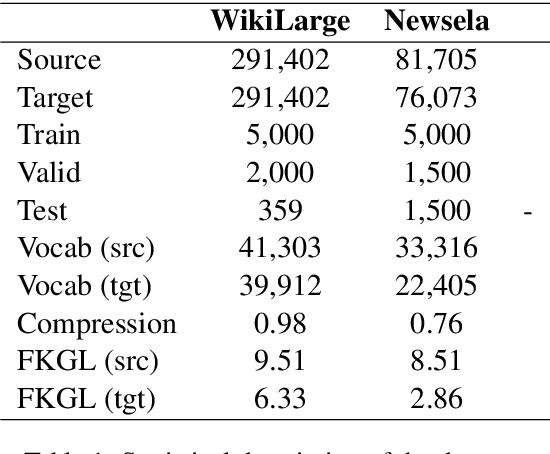
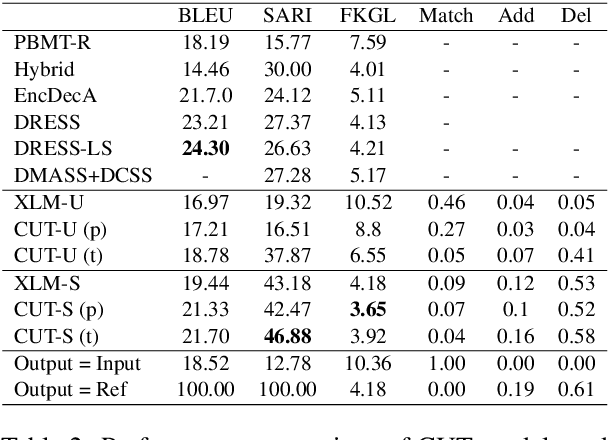
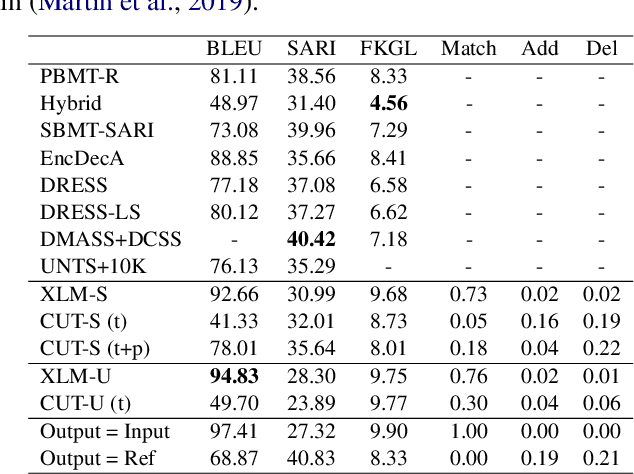
In this paper, we focus on the challenge of learning controllable text simplifications in unsupervised settings. While this problem has been previously discussed for supervised learning algorithms, the literature on the analogies in unsupervised methods is scarse. We propose two unsupervised mechanisms for controlling the output complexity of the generated texts, namely, back translation with control tokens (a learning-based approach) and simplicity-aware beam search (decoding-based approach). We show that by nudging a back-translation algorithm to understand the relative simplicity of a text in comparison to its noisy translation, the algorithm self-supervises itself to produce the output of the desired complexity. This approach achieves competitive performance on well-established benchmarks: SARI score of 46.88% and FKGL of 3.65% on the Newsela dataset.