Online Learning with Sublinear Best-Action Queries

In online learning, a decision maker repeatedly selects one of a set of actions, with the goal of minimizing the overall loss incurred. Following the recent line of research on algorithms endowed with additional predictive features, we revisit this problem by allowing the decision maker to acquire additional information on the actions to be selected. In particular, we study the power of \emph{best-action queries}, which reveal beforehand the identity of the best action at a given time step. In practice, predictive features may be expensive, so we allow the decision maker to issue at most $k$ such queries. We establish tight bounds on the performance any algorithm can achieve when given access to $k$ best-action queries for different types of feedback models. In particular, we prove that in the full feedback model, $k$ queries are enough to achieve an optimal regret of $\Theta\left(\min\left\{\sqrt T, \frac Tk\right\}\right)$. This finding highlights the significant multiplicative advantage in the regret rate achievable with even a modest (sublinear) number $k \in \Omega(\sqrt{T})$ of queries. Additionally, we study the challenging setting in which the only available feedback is obtained during the time steps corresponding to the $k$ best-action queries. There, we provide a tight regret rate of $\Theta\left(\min\left\{\frac{T}{\sqrt k},\frac{T^2}{k^2}\right\}\right)$, which improves over the standard $\Theta\left(\frac{T}{\sqrt k}\right)$ regret rate for label efficient prediction for $k \in \Omega(T^{2/3})$.

The Role of Transparency in Repeated First-Price Auctions with Unknown Valuations

We study the problem of regret minimization for a single bidder in a sequence of first-price auctions where the bidder knows the item's value only if the auction is won. Our main contribution is a complete characterization, up to logarithmic factors, of the minimax regret in terms of the auction's transparency, which regulates the amount of information on competing bids disclosed by the auctioneer at the end of each auction. Our results hold under different assumptions (stochastic, adversarial, and their smoothed variants) on the environment generating the bidder's valuations and competing bids. These minimax rates reveal how the interplay between transparency and the nature of the environment affects how fast one can learn to bid optimally in first-price auctions.

Repeated Bilateral Trade Against a Smoothed Adversary

We study repeated bilateral trade where an adaptive $\sigma$-smooth adversary generates the valuations of sellers and buyers. We provide a complete characterization of the regret regimes for fixed-price mechanisms under different feedback models in the two cases where the learner can post either the same or different prices to buyers and sellers. We begin by showing that the minimax regret after $T$ rounds is of order $\sqrt{T}$ in the full-feedback scenario. Under partial feedback, any algorithm that has to post the same price to buyers and sellers suffers worst-case linear regret. However, when the learner can post two different prices at each round, we design an algorithm enjoying regret of order $T^{3/4}$ ignoring log factors. We prove that this rate is optimal by presenting a surprising $T^{3/4}$ lower bound, which is the main technical contribution of the paper.

Fully Dynamic Online Selection through Online Contention Resolution Schemes

We study fully dynamic online selection problems in an adversarial/stochastic setting that includes Bayesian online selection, prophet inequalities, posted price mechanisms, and stochastic probing problems subject to combinatorial constraints. In the classical ``incremental'' version of the problem, selected elements remain active until the end of the input sequence. On the other hand, in the fully dynamic version of the problem, elements stay active for a limited time interval, and then leave. This models, for example, the online matching of tasks to workers with task/worker-dependent working times, and sequential posted pricing of perishable goods. A successful approach to online selection problems in the adversarial setting is given by the notion of Online Contention Resolution Scheme (OCRS), that uses a priori information to formulate a linear relaxation of the underlying optimization problem, whose optimal fractional solution is rounded online for any adversarial order of the input sequence. Our main contribution is providing a general method for constructing an OCRS for fully dynamic online selection problems. Then, we show how to employ such OCRS to construct no-regret algorithms in a partial information model with semi-bandit feedback and adversarial inputs.

AI-based Data Preparation and Data Analytics in Healthcare: The Case of Diabetes

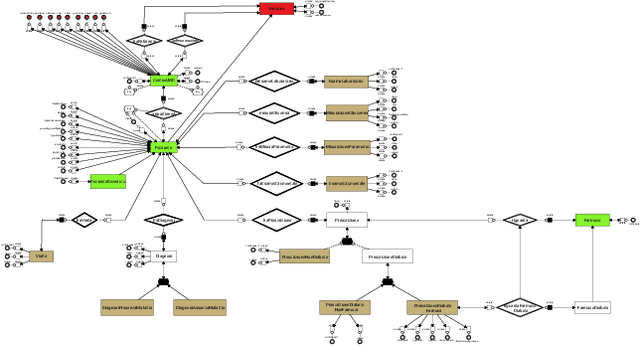
The Associazione Medici Diabetologi (AMD) collects and manages one of the largest worldwide-available collections of diabetic patient records, also known as the AMD database. This paper presents the initial results of an ongoing project whose focus is the application of Artificial Intelligence and Machine Learning techniques for conceptualizing, cleaning, and analyzing such an important and valuable dataset, with the goal of providing predictive insights to better support diabetologists in their diagnostic and therapeutic choices.

Allocating Indivisible Goods to Strategic Agents: Pure Nash Equilibria and Fairness

We consider the problem of fairly allocating a set of indivisible goods to a set of strategic agents with additive valuation functions. We assume no monetary transfers and, therefore, a mechanism in our setting is an algorithm that takes as input the reported -- rather than the true -- values of the agents. Our main goal is to explore whether there exist mechanisms that have pure Nash equilibria for every instance and, at the same time, provide fairness guarantees for the allocations that correspond to these equilibria. We focus on two relaxations of envy-freeness, namely envy-freeness up to one good (EF1), and envy-freeness up to any good (EFX), and we positively answer the above question. In particular, we study two algorithms that are known to produce such allocations in the non-strategic setting: Round-Robin (EF1 allocations for any number of agents) and a cut-and-choose algorithm of Plaut and Roughgarden [SIAM Journal of Discrete Mathematics, 2020] (EFX allocations for two agents). For Round-Robin we show that all of its pure Nash equilibria induce allocations that are EF1 with respect to the underlying true values, while for the algorithm of Plaut and Roughgarden we show that the corresponding allocations not only are EFX but also satisfy maximin share fairness, something that is not true for this algorithm in the non-strategic setting! Further, we show that a weaker version of the latter result holds for any mechanism for two agents that always has pure Nash equilibria which all induce EFX allocations.

Bilateral Trade: A Regret Minimization Perspective

Bilateral trade, a fundamental topic in economics, models the problem of intermediating between two strategic agents, a seller and a buyer, willing to trade a good for which they hold private valuations. In this paper, we cast the bilateral trade problem in a regret minimization framework over $T$ rounds of seller/buyer interactions, with no prior knowledge on their private valuations. Our main contribution is a complete characterization of the regret regimes for fixed-price mechanisms with different feedback models and private valuations, using as a benchmark the best fixed-price in hindsight. More precisely, we prove the following tight bounds on the regret: - $\Theta(\sqrt{T})$ for full-feedback (i.e., direct revelation mechanisms). - $\Theta(T^{2/3})$ for realistic feedback (i.e., posted-price mechanisms) and independent seller/buyer valuations with bounded densities. - $\Theta(T)$ for realistic feedback and seller/buyer valuations with bounded densities. - $\Theta(T)$ for realistic feedback and independent seller/buyer valuations. - $\Theta(T)$ for the adversarial setting.

Humans as Path-Finders for Safe Navigation

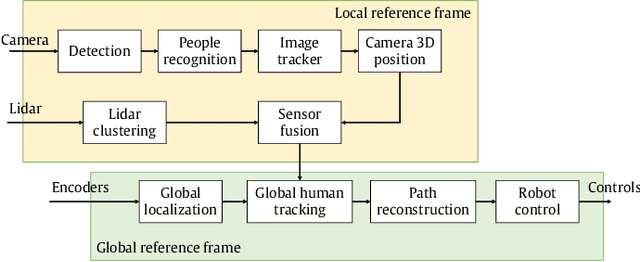
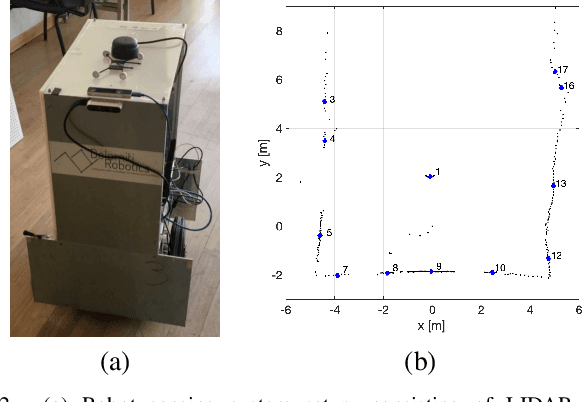
One of the most important barriers toward a widespread use of mobile robots in unstructured and human populated work environments is the ability to plan a safe path. In this paper, we propose to delegate this activity to a human operator that walks in front of the robot marking with her/his footsteps the path to be followed. The implementation of this approach requires a high degree of robustness in locating the specific person to be followed (the leader). We propose a three phase approach to fulfil this goal: 1. identification and tracking of the person in the image space, 2. sensor fusion between camera data and laser sensors, 3. point interpolation with continuous curvature curves. The approach is described in the paper and extensively validated with experimental results.

Stochastic Bandits for Multi-platform Budget Optimization in Online Advertising

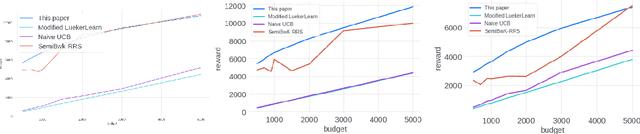
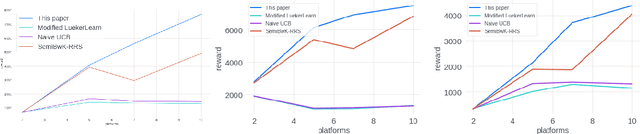
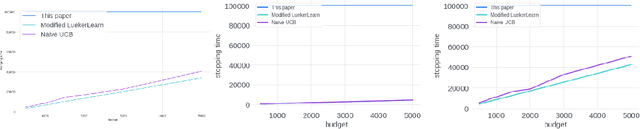
We study the problem of an online advertising system that wants to optimally spend an advertiser's given budget for a campaign across multiple platforms, without knowing the value for showing an ad to the users on those platforms. We model this challenging practical application as a Stochastic Bandits with Knapsacks problem over $T$ rounds of bidding with the set of arms given by the set of distinct bidding $m$-tuples, where $m$ is the number of platforms. We modify the algorithm proposed in Badanidiyuru \emph{et al.,} to extend it to the case of multiple platforms to obtain an algorithm for both the discrete and continuous bid-spaces. Namely, for discrete bid spaces we give an algorithm with regret $O\left(OPT \sqrt {\frac{mn}{B} }+ \sqrt{mn OPT}\right)$, where $OPT$ is the performance of the optimal algorithm that knows the distributions. For continuous bid spaces the regret of our algorithm is $\tilde{O}\left(m^{1/3} \cdot \min\left\{ B^{2/3}, (m T)^{2/3} \right\} \right)$. When restricted to this special-case, this bound improves over Sankararaman and Slivkins in the regime $OPT \ll T$, as is the case in the particular application at hand. Second, we show an $ \Omega\left (\sqrt {m OPT} \right)$ lower bound for the discrete case and an $\Omega\left( m^{1/3} B^{2/3}\right)$ lower bound for the continuous setting, almost matching the upper bounds. Finally, we use a real-world data set from a large internet online advertising company with multiple ad platforms and show that our algorithms outperform common benchmarks and satisfy the required properties warranted in the real-world application.

Submodular Maximization subject to a Knapsack Constraint: Combinatorial Algorithms with Near-optimal Adaptive Complexity

The growing need to deal with massive instances motivates the design of algorithms balancing the quality of the solution with applicability. For the latter, an important measure is the \emph{adaptive complexity}, capturing the number of sequential rounds of parallel computation needed. In this work we obtain the first \emph{constant factor} approximation algorithm for non-monotone submodular maximization subject to a knapsack constraint with \emph{near-optimal} $O(\log n)$ adaptive complexity. Low adaptivity by itself, however, is not enough: one needs to account for the total number of function evaluations (or value queries) as well. Our algorithm asks $\tilde{O}(n^2)$ value queries, but can be modified to run with only $\tilde{O}(n)$ instead, while retaining a low adaptive complexity of $O(\log^2n)$. Besides the above improvement in adaptivity, this is also the first \emph{combinatorial} approach with sublinear adaptive complexity for the problem and yields algorithms comparable to the state-of-the-art even for the special cases of cardinality constraints or monotone objectives. Finally, we showcase our algorithms' applicability on real-world datasets.