Riccardo Colini-Baldeschi
Fully Dynamic Online Selection through Online Contention Resolution Schemes
Jan 08, 2023
Abstract:We study fully dynamic online selection problems in an adversarial/stochastic setting that includes Bayesian online selection, prophet inequalities, posted price mechanisms, and stochastic probing problems subject to combinatorial constraints. In the classical ``incremental'' version of the problem, selected elements remain active until the end of the input sequence. On the other hand, in the fully dynamic version of the problem, elements stay active for a limited time interval, and then leave. This models, for example, the online matching of tasks to workers with task/worker-dependent working times, and sequential posted pricing of perishable goods. A successful approach to online selection problems in the adversarial setting is given by the notion of Online Contention Resolution Scheme (OCRS), that uses a priori information to formulate a linear relaxation of the underlying optimization problem, whose optimal fractional solution is rounded online for any adversarial order of the input sequence. Our main contribution is providing a general method for constructing an OCRS for fully dynamic online selection problems. Then, we show how to employ such OCRS to construct no-regret algorithms in a partial information model with semi-bandit feedback and adversarial inputs.
Stochastic Bandits for Multi-platform Budget Optimization in Online Advertising
Mar 25, 2021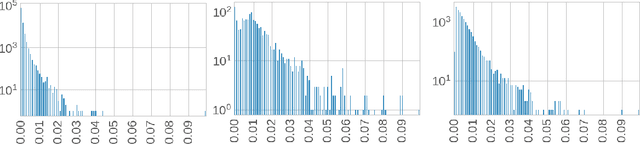
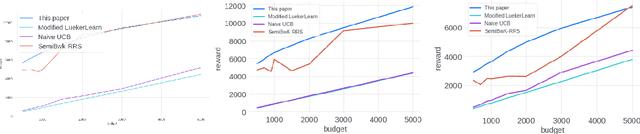
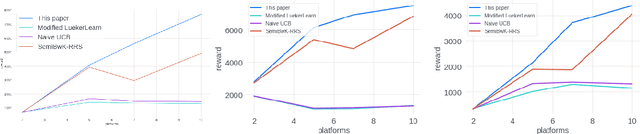
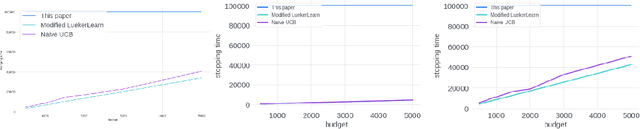
Abstract:We study the problem of an online advertising system that wants to optimally spend an advertiser's given budget for a campaign across multiple platforms, without knowing the value for showing an ad to the users on those platforms. We model this challenging practical application as a Stochastic Bandits with Knapsacks problem over $T$ rounds of bidding with the set of arms given by the set of distinct bidding $m$-tuples, where $m$ is the number of platforms. We modify the algorithm proposed in Badanidiyuru \emph{et al.,} to extend it to the case of multiple platforms to obtain an algorithm for both the discrete and continuous bid-spaces. Namely, for discrete bid spaces we give an algorithm with regret $O\left(OPT \sqrt {\frac{mn}{B} }+ \sqrt{mn OPT}\right)$, where $OPT$ is the performance of the optimal algorithm that knows the distributions. For continuous bid spaces the regret of our algorithm is $\tilde{O}\left(m^{1/3} \cdot \min\left\{ B^{2/3}, (m T)^{2/3} \right\} \right)$. When restricted to this special-case, this bound improves over Sankararaman and Slivkins in the regime $OPT \ll T$, as is the case in the particular application at hand. Second, we show an $ \Omega\left (\sqrt {m OPT} \right)$ lower bound for the discrete case and an $\Omega\left( m^{1/3} B^{2/3}\right)$ lower bound for the continuous setting, almost matching the upper bounds. Finally, we use a real-world data set from a large internet online advertising company with multiple ad platforms and show that our algorithms outperform common benchmarks and satisfy the required properties warranted in the real-world application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge