Multi-Platform Budget Management in Ad Markets with Non-IC Auctions

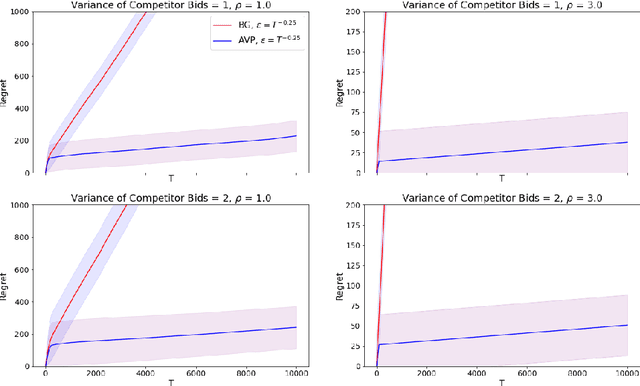
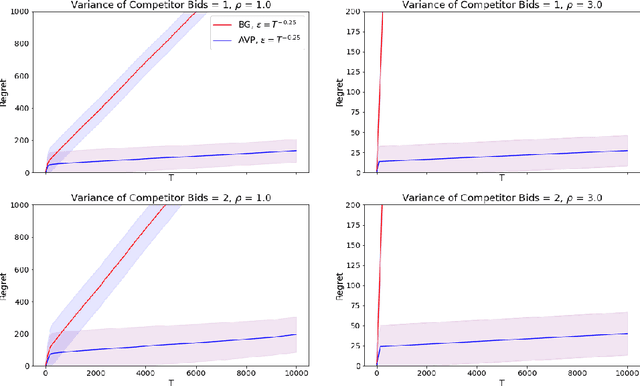
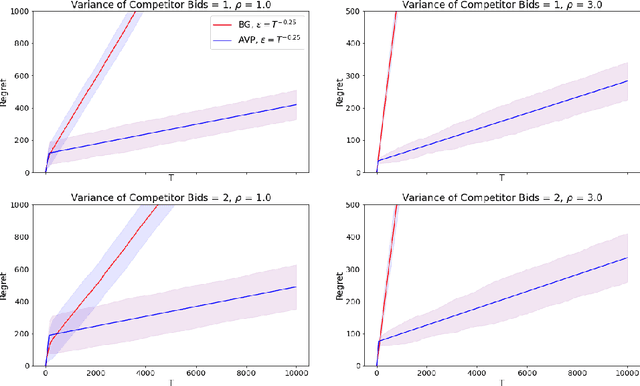
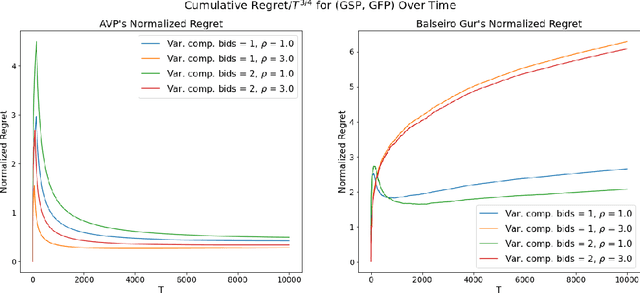
In online advertising markets, budget-constrained advertisers acquire ad placements through repeated bidding in auctions on various platforms. We present a strategy for bidding optimally in a set of auctions that may or may not be incentive-compatible under the presence of budget constraints. Our strategy maximizes the expected total utility across auctions while satisfying the advertiser's budget constraints in expectation. Additionally, we investigate the online setting where the advertiser must submit bids across platforms while learning about other bidders' bids over time. Our algorithm has $O(T^{3/4})$ regret under the full-information setting. Finally, we demonstrate that our algorithms have superior cumulative regret on both synthetic and real-world datasets of ad placement auctions, compared to existing adaptive pacing algorithms.

Optimal Spend Rate Estimation and Pacing for Ad Campaigns with Budgets

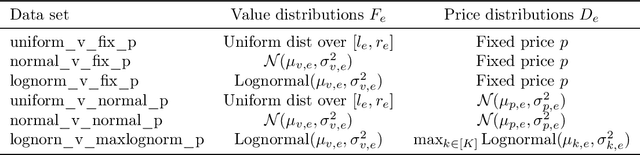
Online ad platforms offer budget management tools for advertisers that aim to maximize the number of conversions given a budget constraint. As the volume of impressions, conversion rates and prices vary over time, these budget management systems learn a spend plan (to find the optimal distribution of budget over time) and run a pacing algorithm which follows the spend plan. This paper considers two models for impressions and competition that varies with time: a) an episodic model which exhibits stationarity in each episode, but each episode can be arbitrarily different from the next, and b) a model where the distributions of prices and values change slowly over time. We present the first learning theoretic guarantees on both the accuracy of spend plans and the resulting end-to-end budget management system. We present four main results: 1) for the episodic setting we give sample complexity bounds for the spend rate prediction problem: given $n$ samples from each episode, with high probability we have $|\widehat{\rho}_e - \rho_e| \leq \tilde{O}(\frac{1}{n^{1/3}})$ where $\rho_e$ is the optimal spend rate for the episode, $\widehat{\rho}_e$ is the estimate from our algorithm, 2) we extend the algorithm of Balseiro and Gur (2017) to operate on varying, approximate spend rates and show that the resulting combined system of optimal spend rate estimation and online pacing algorithm for episodic settings has regret that vanishes in number of historic samples $n$ and the number of rounds $T$, 3) for non-episodic but slowly-changing distributions we show that the same approach approximates the optimal bidding strategy up to a factor dependent on the rate-of-change of the distributions and 4) we provide experiments showing that our algorithm outperforms both static spend plans and non-pacing across a wide variety of settings.

Stochastic Bandits for Multi-platform Budget Optimization in Online Advertising

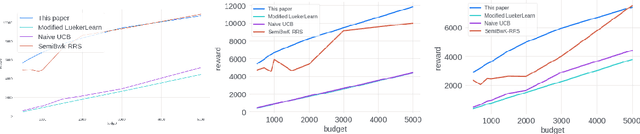
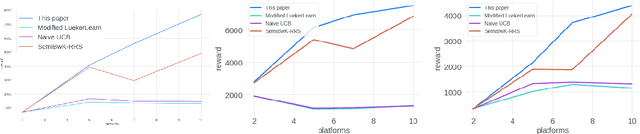
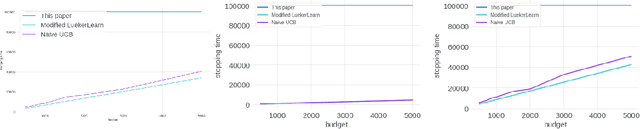
We study the problem of an online advertising system that wants to optimally spend an advertiser's given budget for a campaign across multiple platforms, without knowing the value for showing an ad to the users on those platforms. We model this challenging practical application as a Stochastic Bandits with Knapsacks problem over $T$ rounds of bidding with the set of arms given by the set of distinct bidding $m$-tuples, where $m$ is the number of platforms. We modify the algorithm proposed in Badanidiyuru \emph{et al.,} to extend it to the case of multiple platforms to obtain an algorithm for both the discrete and continuous bid-spaces. Namely, for discrete bid spaces we give an algorithm with regret $O\left(OPT \sqrt {\frac{mn}{B} }+ \sqrt{mn OPT}\right)$, where $OPT$ is the performance of the optimal algorithm that knows the distributions. For continuous bid spaces the regret of our algorithm is $\tilde{O}\left(m^{1/3} \cdot \min\left\{ B^{2/3}, (m T)^{2/3} \right\} \right)$. When restricted to this special-case, this bound improves over Sankararaman and Slivkins in the regime $OPT \ll T$, as is the case in the particular application at hand. Second, we show an $ \Omega\left (\sqrt {m OPT} \right)$ lower bound for the discrete case and an $\Omega\left( m^{1/3} B^{2/3}\right)$ lower bound for the continuous setting, almost matching the upper bounds. Finally, we use a real-world data set from a large internet online advertising company with multiple ad platforms and show that our algorithms outperform common benchmarks and satisfy the required properties warranted in the real-world application.