Multi-Platform Budget Management in Ad Markets with Non-IC Auctions

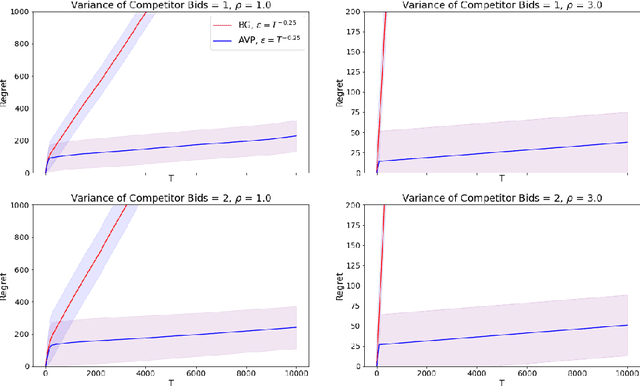
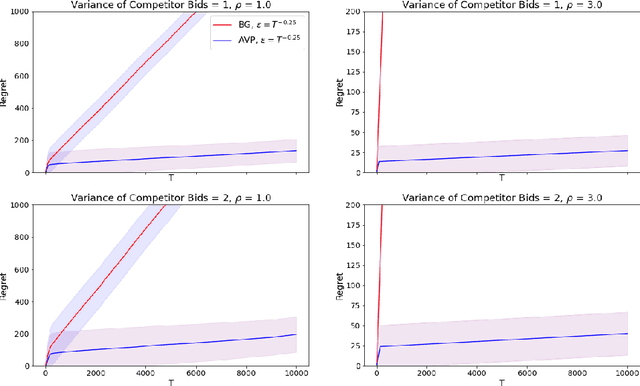
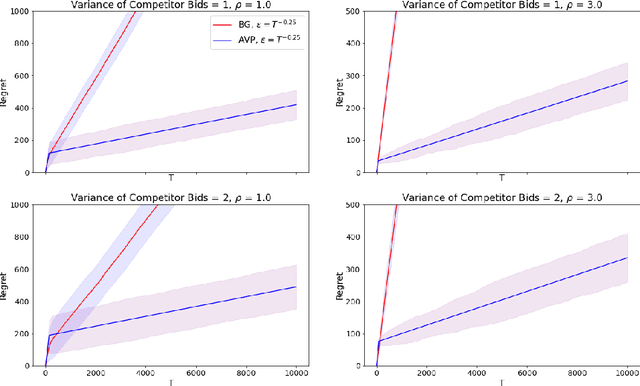
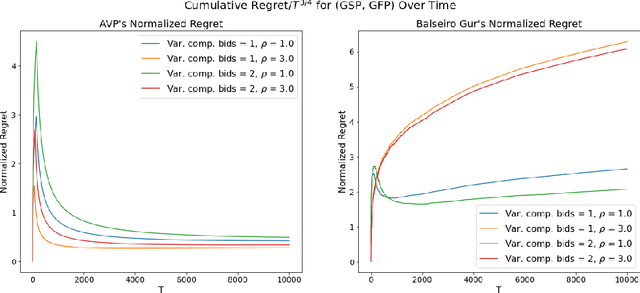
In online advertising markets, budget-constrained advertisers acquire ad placements through repeated bidding in auctions on various platforms. We present a strategy for bidding optimally in a set of auctions that may or may not be incentive-compatible under the presence of budget constraints. Our strategy maximizes the expected total utility across auctions while satisfying the advertiser's budget constraints in expectation. Additionally, we investigate the online setting where the advertiser must submit bids across platforms while learning about other bidders' bids over time. Our algorithm has $O(T^{3/4})$ regret under the full-information setting. Finally, we demonstrate that our algorithms have superior cumulative regret on both synthetic and real-world datasets of ad placement auctions, compared to existing adaptive pacing algorithms.

Active Learning for Non-Parametric Choice Models

We study the problem of actively learning a non-parametric choice model based on consumers' decisions. We present a negative result showing that such choice models may not be identifiable. To overcome the identifiability problem, we introduce a directed acyclic graph (DAG) representation of the choice model, which in a sense captures as much information about the choice model as could information-theoretically be identified. We then consider the problem of learning an approximation to this DAG representation in an active-learning setting. We design an efficient active-learning algorithm to estimate the DAG representation of the non-parametric choice model, which runs in polynomial time when the set of frequent rankings is drawn uniformly at random. Our algorithm learns the distribution over the most popular items of frequent preferences by actively and repeatedly offering assortments of items and observing the item chosen. We show that our algorithm can better recover a set of frequent preferences on both a synthetic and publicly available dataset on consumers' preferences, compared to the corresponding non-active learning estimation algorithms. This demonstrates the value of our algorithm and active-learning approaches more generally.

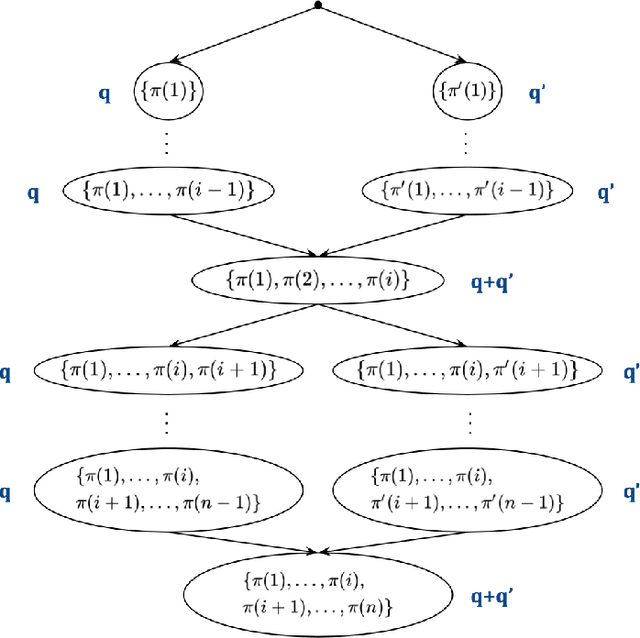
Online Learning via Offline Greedy Algorithms: Applications in Market Design and Optimization

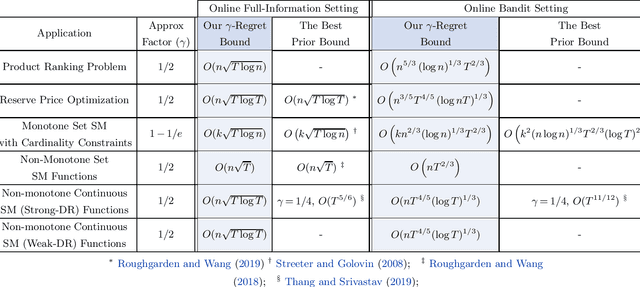
Motivated by online decision-making in time-varying combinatorial environments, we study the problem of transforming offline algorithms to their online counterparts. We focus on offline combinatorial problems that are amenable to a constant factor approximation using a greedy algorithm that is robust to local errors. For such problems, we provide a general framework that efficiently transforms offline robust greedy algorithms to online ones using Blackwell approachability. We show that the resulting online algorithms have $O(\sqrt{T})$ (approximate) regret under the full information setting. We further introduce a bandit extension of Blackwell approachability that we call Bandit Blackwell approachability. We leverage this notion to transform greedy robust offline algorithms into a $O(T^{2/3})$ (approximate) regret in the bandit setting. Demonstrating the flexibility of our framework, we apply our offline-to-online transformation to several problems at the intersection of revenue management, market design, and online optimization, including product ranking optimization in online platforms, reserve price optimization in auctions, and submodular maximization. We show that our transformation, when applied to these applications, leads to new regret bounds or improves the current known bounds.