Learning in Repeated Multi-Unit Pay-As-Bid Auctions

Motivated by Carbon Emissions Trading Schemes, Treasury Auctions, and Procurement Auctions, which all involve the auctioning of homogeneous multiple units, we consider the problem of learning how to bid in repeated multi-unit pay-as-bid auctions. In each of these auctions, a large number of (identical) items are to be allocated to the largest submitted bids, where the price of each of the winning bids is equal to the bid itself. The problem of learning how to bid in pay-as-bid auctions is challenging due to the combinatorial nature of the action space. We overcome this challenge by focusing on the offline setting, where the bidder optimizes their vector of bids while only having access to the past submitted bids by other bidders. We show that the optimal solution to the offline problem can be obtained using a polynomial time dynamic programming (DP) scheme. We leverage the structure of the DP scheme to design online learning algorithms with polynomial time and space complexity under full information and bandit feedback settings. We achieve an upper bound on regret of $O(M\sqrt{T\log |\mathcal{B}|})$ and $O(M\sqrt{|\mathcal{B}|T\log |\mathcal{B}|})$ respectively, where $M$ is the number of units demanded by the bidder, $T$ is the total number of auctions, and $|\mathcal{B}|$ is the size of the discretized bid space. We accompany these results with a regret lower bound, which match the linear dependency in $M$. Our numerical results suggest that when all agents behave according to our proposed no regret learning algorithms, the resulting market dynamics mainly converge to a welfare maximizing equilibrium where bidders submit uniform bids. Lastly, our experiments demonstrate that the pay-as-bid auction consistently generates significantly higher revenue compared to its popular alternative, the uniform price auction.

Online Resource Allocation with Convex-set Machine-Learned Advice

Decision-makers often have access to a machine-learned prediction about demand, referred to as advice, which can potentially be utilized in online decision-making processes for resource allocation. However, exploiting such advice poses challenges due to its potential inaccuracy. To address this issue, we propose a framework that enhances online resource allocation decisions with potentially unreliable machine-learned (ML) advice. We assume here that this advice is represented by a general convex uncertainty set for the demand vector. We introduce a parameterized class of Pareto optimal online resource allocation algorithms that strike a balance between consistent and robust ratios. The consistent ratio measures the algorithm's performance (compared to the optimal hindsight solution) when the ML advice is accurate, while the robust ratio captures performance under an adversarial demand process when the advice is inaccurate. Specifically, in a C-Pareto optimal setting, we maximize the robust ratio while ensuring that the consistent ratio is at least C. Our proposed C-Pareto optimal algorithm is an adaptive protection level algorithm, which extends the classical fixed protection level algorithm introduced in Littlewood (2005) and Ball and Queyranne (2009). Solving a complex non-convex continuous optimization problem characterizes the adaptive protection level algorithm. To complement our algorithms, we present a simple method for computing the maximum achievable consistent ratio, which serves as an estimate for the maximum value of the ML advice. Additionally, we present numerical studies to evaluate the performance of our algorithm in comparison to benchmark algorithms. The results demonstrate that by adjusting the parameter C, our algorithms effectively strike a balance between worst-case and average performance, outperforming the benchmark algorithms.

Multi-Platform Budget Management in Ad Markets with Non-IC Auctions

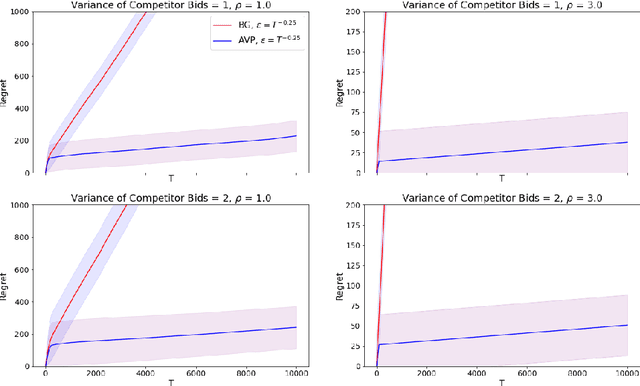
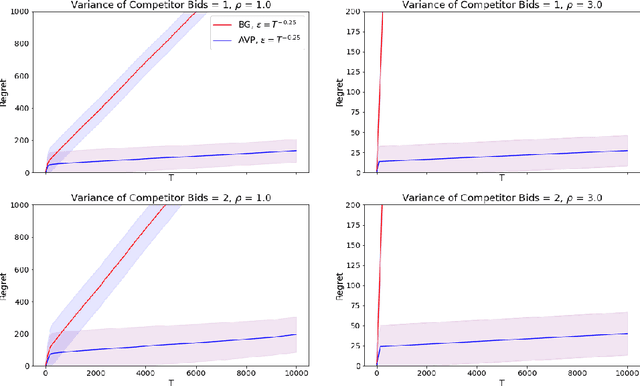
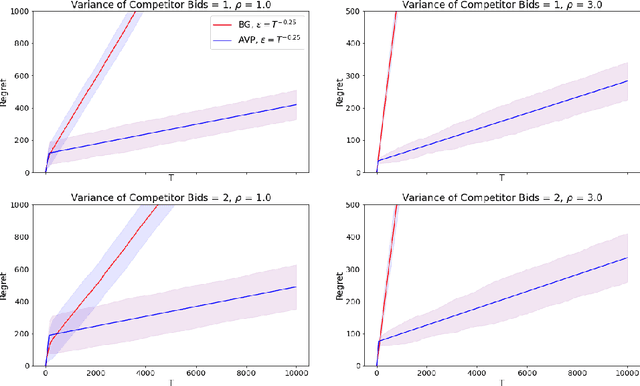
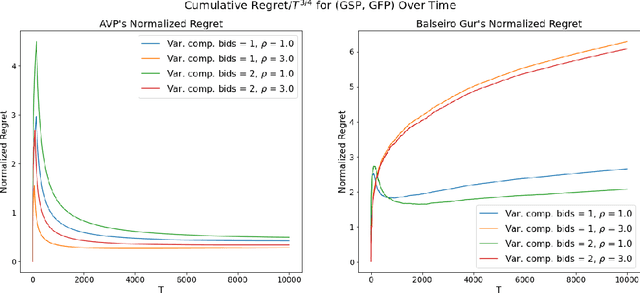
In online advertising markets, budget-constrained advertisers acquire ad placements through repeated bidding in auctions on various platforms. We present a strategy for bidding optimally in a set of auctions that may or may not be incentive-compatible under the presence of budget constraints. Our strategy maximizes the expected total utility across auctions while satisfying the advertiser's budget constraints in expectation. Additionally, we investigate the online setting where the advertiser must submit bids across platforms while learning about other bidders' bids over time. Our algorithm has $O(T^{3/4})$ regret under the full-information setting. Finally, we demonstrate that our algorithms have superior cumulative regret on both synthetic and real-world datasets of ad placement auctions, compared to existing adaptive pacing algorithms.

Interpolating Item and User Fairness in Recommendation Systems

Online platforms employ recommendation systems to enhance customer engagement and drive revenue. However, in a multi-sided platform where the platform interacts with diverse stakeholders such as sellers (items) and customers (users), each with their own desired outcomes, finding an appropriate middle ground becomes a complex operational challenge. In this work, we investigate the ``price of fairness'', which captures the platform's potential compromises when balancing the interests of different stakeholders. Motivated by this, we propose a fair recommendation framework where the platform maximizes its revenue while interpolating between item and user fairness constraints. We further examine the fair recommendation problem in a more realistic yet challenging online setting, where the platform lacks knowledge of user preferences and can only observe binary purchase decisions. To address this, we design a low-regret online optimization algorithm that preserves the platform's revenue while achieving fairness for both items and users. Finally, we demonstrate the effectiveness of our framework and proposed method via a case study on MovieLens data.

Online Learning in Multi-unit Auctions

We consider repeated multi-unit auctions with uniform pricing, which are widely used in practice for allocating goods such as carbon licenses. In each round, $K$ identical units of a good are sold to a group of buyers that have valuations with diminishing marginal returns. The buyers submit bids for the units, and then a price $p$ is set per unit so that all the units are sold. We consider two variants of the auction, where the price is set to the $K$-th highest bid and $(K+1)$-st highest bid, respectively. We analyze the properties of this auction in both the offline and online settings. In the offline setting, we consider the problem that one player $i$ is facing: given access to a data set that contains the bids submitted by competitors in past auctions, find a bid vector that maximizes player $i$'s cumulative utility on the data set. We design a polynomial time algorithm for this problem, by showing it is equivalent to finding a maximum-weight path on a carefully constructed directed acyclic graph. In the online setting, the players run learning algorithms to update their bids as they participate in the auction over time. Based on our offline algorithm, we design efficient online learning algorithms for bidding. The algorithms have sublinear regret, under both full information and bandit feedback structures. We complement our online learning algorithms with regret lower bounds. Finally, we analyze the quality of the equilibria in the worst case through the lens of the core solution concept in the game among the bidders. We show that the $(K+1)$-st price format is susceptible to collusion among the bidders; meanwhile, the $K$-th price format does not have this issue.

Multi-channel Autobidding with Budget and ROI Constraints

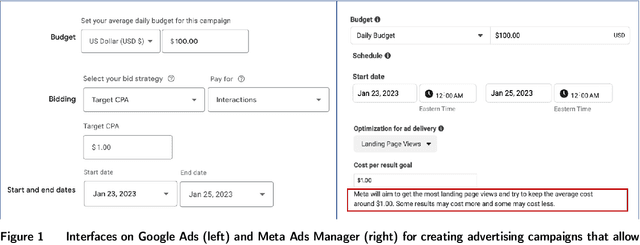
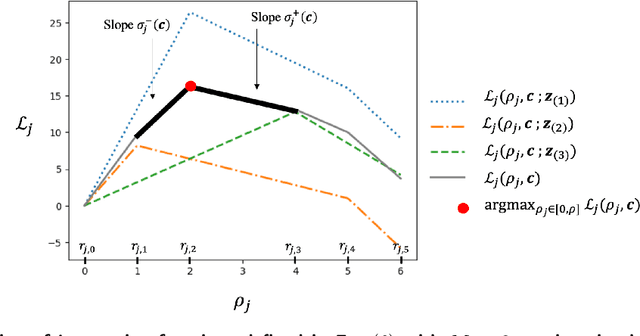
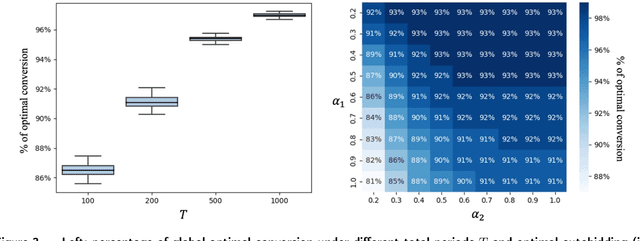
In digital online advertising, advertisers procure ad impressions simultaneously on multiple platforms, or so-called channels, such as Google Ads, Meta Ads Manager, etc., each of which consists of numerous ad auctions. We study how an advertiser maximizes total conversion (e.g. ad clicks) while satisfying aggregate return-on-investment (ROI) and budget constraints across all channels. In practice, an advertiser does not have control over, and thus cannot globally optimize, which individual ad auctions she participates in for each channel, and instead authorizes a channel to procure impressions on her behalf: the advertiser can only utilize two levers on each channel, namely setting a per-channel budget and per-channel target ROI. In this work, we first analyze the effectiveness of each of these levers for solving the advertiser's global multi-channel problem. We show that when an advertiser only optimizes over per-channel ROIs, her total conversion can be arbitrarily worse than what she could have obtained in the global problem. Further, we show that the advertiser can achieve the global optimal conversion when she only optimizes over per-channel budgets. In light of this finding, under a bandit feedback setting that mimics real-world scenarios where advertisers have limited information on ad auctions in each channels and how channels procure ads, we present an efficient learning algorithm that produces per-channel budgets whose resulting conversion approximates that of the global optimal problem. Finally, we argue that all our results hold for both single-item and multi-item auctions from which channels procure impressions on advertisers' behalf.

Dynamic Bandits with an Auto-Regressive Temporal Structure

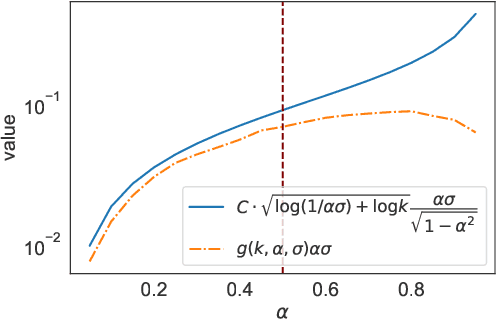
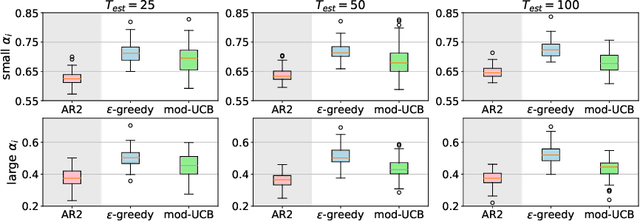
Multi-armed bandit (MAB) problems are mainly studied under two extreme settings known as stochastic and adversarial. These two settings, however, do not capture realistic environments such as search engines and marketing and advertising, in which rewards stochastically change in time. Motivated by that, we introduce and study a dynamic MAB problem with stochastic temporal structure, where the expected reward of each arm is governed by an auto-regressive (AR) model. Due to the dynamic nature of the rewards, simple "explore and commit" policies fail, as all arms have to be explored continuously over time. We formalize this by characterizing a per-round regret lower bound, where the regret is measured against a strong (dynamic) benchmark. We then present an algorithm whose per-round regret almost matches our regret lower bound. Our algorithm relies on two mechanisms: (i) alternating between recently pulled arms and unpulled arms with potential, and (ii) restarting. These mechanisms enable the algorithm to dynamically adapt to changes and discard irrelevant past information at a suitable rate. In numerical studies, we further demonstrate the strength of our algorithm under different types of non-stationary settings.

Active Learning for Non-Parametric Choice Models

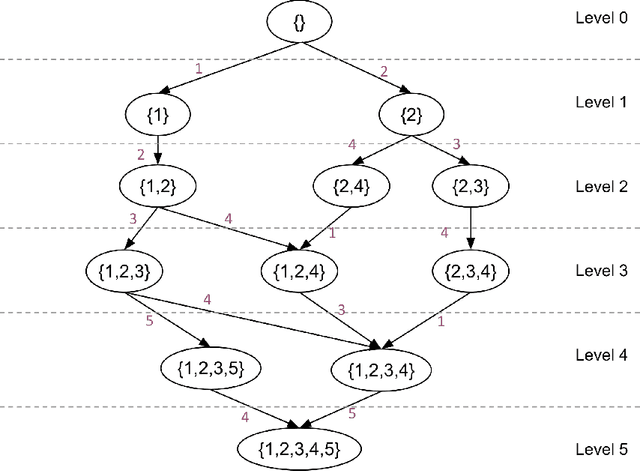
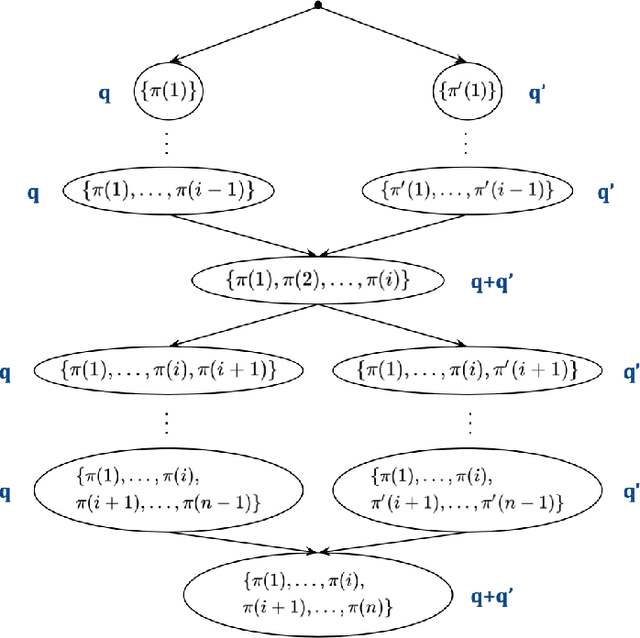
We study the problem of actively learning a non-parametric choice model based on consumers' decisions. We present a negative result showing that such choice models may not be identifiable. To overcome the identifiability problem, we introduce a directed acyclic graph (DAG) representation of the choice model, which in a sense captures as much information about the choice model as could information-theoretically be identified. We then consider the problem of learning an approximation to this DAG representation in an active-learning setting. We design an efficient active-learning algorithm to estimate the DAG representation of the non-parametric choice model, which runs in polynomial time when the set of frequent rankings is drawn uniformly at random. Our algorithm learns the distribution over the most popular items of frequent preferences by actively and repeatedly offering assortments of items and observing the item chosen. We show that our algorithm can better recover a set of frequent preferences on both a synthetic and publicly available dataset on consumers' preferences, compared to the corresponding non-active learning estimation algorithms. This demonstrates the value of our algorithm and active-learning approaches more generally.

Online Learning via Offline Greedy Algorithms: Applications in Market Design and Optimization

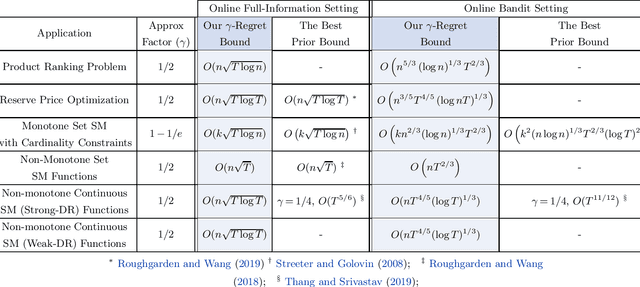
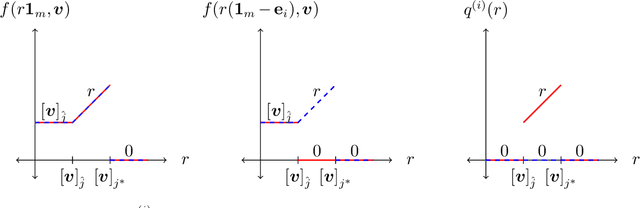
Motivated by online decision-making in time-varying combinatorial environments, we study the problem of transforming offline algorithms to their online counterparts. We focus on offline combinatorial problems that are amenable to a constant factor approximation using a greedy algorithm that is robust to local errors. For such problems, we provide a general framework that efficiently transforms offline robust greedy algorithms to online ones using Blackwell approachability. We show that the resulting online algorithms have $O(\sqrt{T})$ (approximate) regret under the full information setting. We further introduce a bandit extension of Blackwell approachability that we call Bandit Blackwell approachability. We leverage this notion to transform greedy robust offline algorithms into a $O(T^{2/3})$ (approximate) regret in the bandit setting. Demonstrating the flexibility of our framework, we apply our offline-to-online transformation to several problems at the intersection of revenue management, market design, and online optimization, including product ranking optimization in online platforms, reserve price optimization in auctions, and submodular maximization. We show that our transformation, when applied to these applications, leads to new regret bounds or improves the current known bounds.

Learning Product Rankings Robust to Fake Users

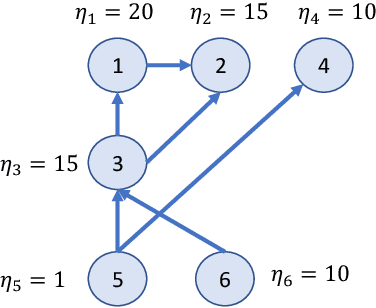
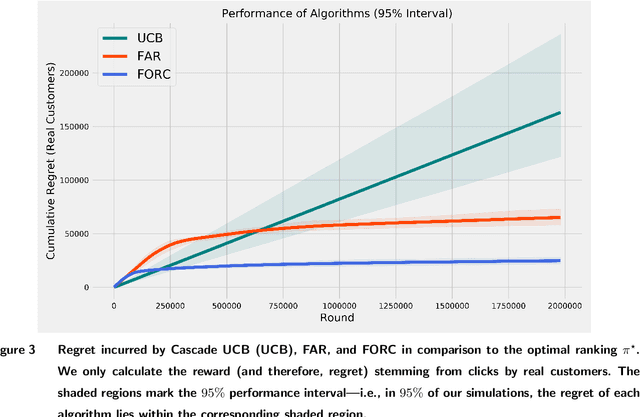
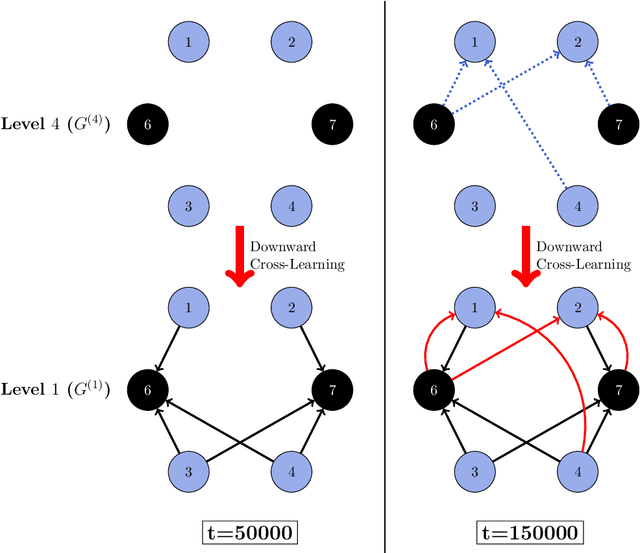
In many online platforms, customers' decisions are substantially influenced by product rankings as most customers only examine a few top-ranked products. Concurrently, such platforms also use the same data corresponding to customers' actions to learn how these products must be ranked or ordered. These interactions in the underlying learning process, however, may incentivize sellers to artificially inflate their position by employing fake users, as exemplified by the emergence of click farms. Motivated by such fraudulent behavior, we study the ranking problem of a platform that faces a mixture of real and fake users who are indistinguishable from one another. We first show that existing learning algorithms---that are optimal in the absence of fake users---may converge to highly sub-optimal rankings under manipulation by fake users. To overcome this deficiency, we develop efficient learning algorithms under two informational environments: in the first setting, the platform is aware of the number of fake users, and in the second setting, it is agnostic to the number of fake users. For both these environments, we prove that our algorithms converge to the optimal ranking, while being robust to the aforementioned fraudulent behavior; we also present worst-case performance guarantees for our methods, and show that they significantly outperform existing algorithms. At a high level, our work employs several novel approaches to guarantee robustness such as: (i) constructing product-ordering graphs that encode the pairwise relationships between products inferred from the customers' actions; and (ii) implementing multiple levels of learning with a judicious amount of bi-directional cross-learning between levels.