Dynamic Bandits with an Auto-Regressive Temporal Structure

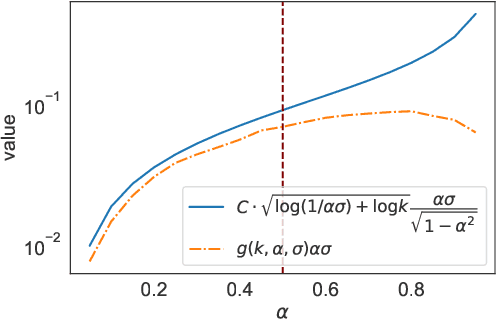
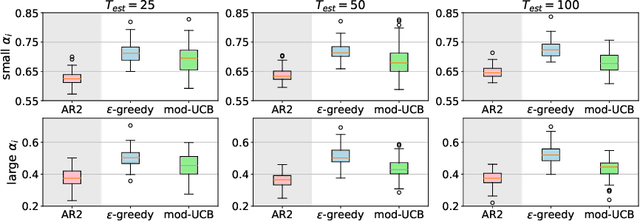
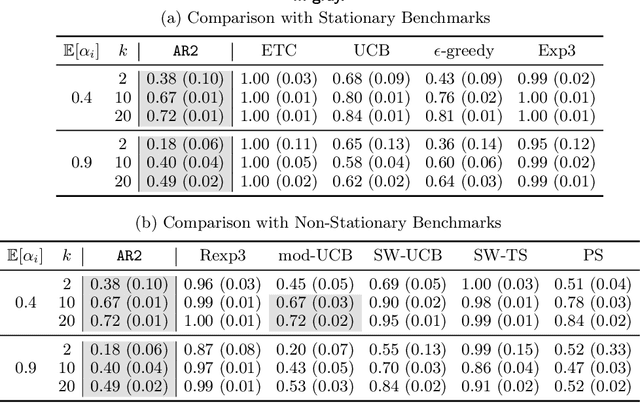
Multi-armed bandit (MAB) problems are mainly studied under two extreme settings known as stochastic and adversarial. These two settings, however, do not capture realistic environments such as search engines and marketing and advertising, in which rewards stochastically change in time. Motivated by that, we introduce and study a dynamic MAB problem with stochastic temporal structure, where the expected reward of each arm is governed by an auto-regressive (AR) model. Due to the dynamic nature of the rewards, simple "explore and commit" policies fail, as all arms have to be explored continuously over time. We formalize this by characterizing a per-round regret lower bound, where the regret is measured against a strong (dynamic) benchmark. We then present an algorithm whose per-round regret almost matches our regret lower bound. Our algorithm relies on two mechanisms: (i) alternating between recently pulled arms and unpulled arms with potential, and (ii) restarting. These mechanisms enable the algorithm to dynamically adapt to changes and discard irrelevant past information at a suitable rate. In numerical studies, we further demonstrate the strength of our algorithm under different types of non-stationary settings.