Learning Universal User Representations Leveraging Cross-domain User Intent at Snapchat

The development of powerful user representations is a key factor in the success of recommender systems (RecSys). Online platforms employ a range of RecSys techniques to personalize user experience across diverse in-app surfaces. User representations are often learned individually through user's historical interactions within each surface and user representations across different surfaces can be shared post-hoc as auxiliary features or additional retrieval sources. While effective, such schemes cannot directly encode collaborative filtering signals across different surfaces, hindering its capacity to discover complex relationships between user behaviors and preferences across the whole platform. To bridge this gap at Snapchat, we seek to conduct universal user modeling (UUM) across different in-app surfaces, learning general-purpose user representations which encode behaviors across surfaces. Instead of replacing domain-specific representations, UUM representations capture cross-domain trends, enriching existing representations with complementary information. This work discusses our efforts in developing initial UUM versions, practical challenges, technical choices and modeling and research directions with promising offline performance. Following successful A/B testing, UUM representations have been launched in production, powering multiple use cases and demonstrating their value. UUM embedding has been incorporated into (i) Long-form Video embedding-based retrieval, leading to 2.78% increase in Long-form Video Open Rate, (ii) Long-form Video L2 ranking, with 19.2% increase in Long-form Video View Time sum, (iii) Lens L2 ranking, leading to 1.76% increase in Lens play time, and (iv) Notification L2 ranking, with 0.87% increase in Notification Open Rate.

On the Robustness of Epoch-Greedy in Multi-Agent Contextual Bandit Mechanisms

Efficient learning in multi-armed bandit mechanisms such as pay-per-click (PPC) auctions typically involves three challenges: 1) inducing truthful bidding behavior (incentives), 2) using personalization in the users (context), and 3) circumventing manipulations in click patterns (corruptions). Each of these challenges has been studied orthogonally in the literature; incentives have been addressed by a line of work on truthful multi-armed bandit mechanisms, context has been extensively tackled by contextual bandit algorithms, while corruptions have been discussed via a recent line of work on bandits with adversarial corruptions. Since these challenges co-exist, it is important to understand the robustness of each of these approaches in addressing the other challenges, provide algorithms that can handle all simultaneously, and highlight inherent limitations in this combination. In this work, we show that the most prominent contextual bandit algorithm, $\epsilon$-greedy can be extended to handle the challenges introduced by strategic arms in the contextual multi-arm bandit mechanism setting. We further show that $\epsilon$-greedy is inherently robust to adversarial data corruption attacks and achieves performance that degrades linearly with the amount of corruption.

Optimal Spend Rate Estimation and Pacing for Ad Campaigns with Budgets

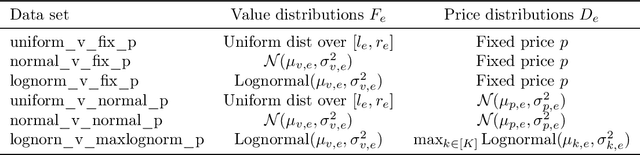
Online ad platforms offer budget management tools for advertisers that aim to maximize the number of conversions given a budget constraint. As the volume of impressions, conversion rates and prices vary over time, these budget management systems learn a spend plan (to find the optimal distribution of budget over time) and run a pacing algorithm which follows the spend plan. This paper considers two models for impressions and competition that varies with time: a) an episodic model which exhibits stationarity in each episode, but each episode can be arbitrarily different from the next, and b) a model where the distributions of prices and values change slowly over time. We present the first learning theoretic guarantees on both the accuracy of spend plans and the resulting end-to-end budget management system. We present four main results: 1) for the episodic setting we give sample complexity bounds for the spend rate prediction problem: given $n$ samples from each episode, with high probability we have $|\widehat{\rho}_e - \rho_e| \leq \tilde{O}(\frac{1}{n^{1/3}})$ where $\rho_e$ is the optimal spend rate for the episode, $\widehat{\rho}_e$ is the estimate from our algorithm, 2) we extend the algorithm of Balseiro and Gur (2017) to operate on varying, approximate spend rates and show that the resulting combined system of optimal spend rate estimation and online pacing algorithm for episodic settings has regret that vanishes in number of historic samples $n$ and the number of rounds $T$, 3) for non-episodic but slowly-changing distributions we show that the same approach approximates the optimal bidding strategy up to a factor dependent on the rate-of-change of the distributions and 4) we provide experiments showing that our algorithm outperforms both static spend plans and non-pacing across a wide variety of settings.