Variational and Explanatory Neural Networks for Encoding Cancer Profiles and Predicting Drug Responses

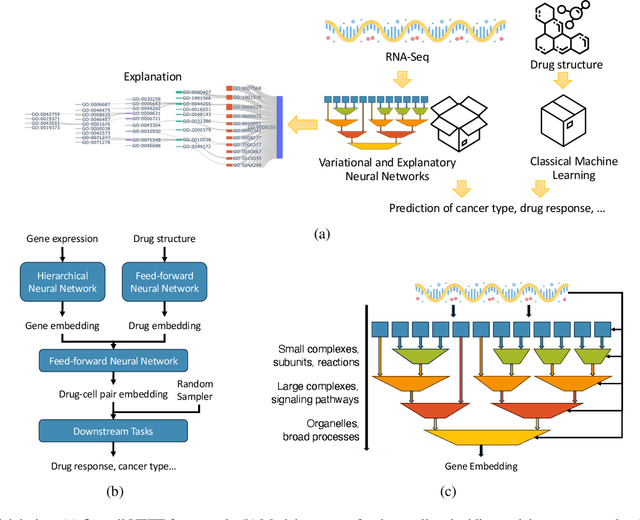
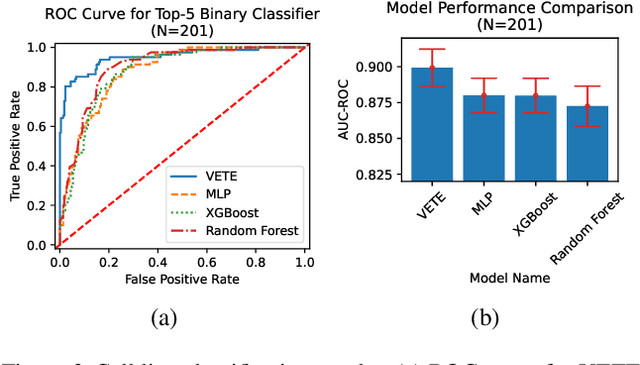
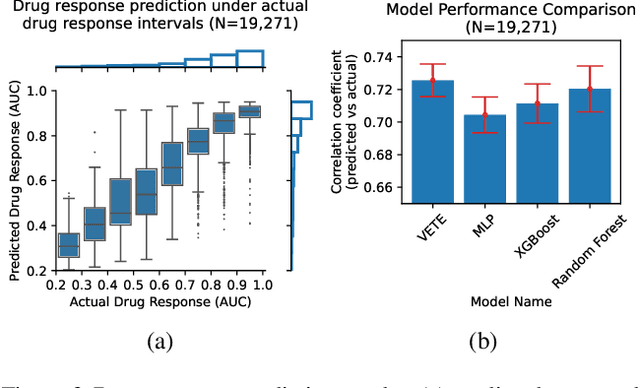
Human cancers present a significant public health challenge and require the discovery of novel drugs through translational research. Transcriptomics profiling data that describes molecular activities in tumors and cancer cell lines are widely utilized for predicting anti-cancer drug responses. However, existing AI models face challenges due to noise in transcriptomics data and lack of biological interpretability. To overcome these limitations, we introduce VETE (Variational and Explanatory Transcriptomics Encoder), a novel neural network framework that incorporates a variational component to mitigate noise effects and integrates traceable gene ontology into the neural network architecture for encoding cancer transcriptomics data. Key innovations include a local interpretability-guided method for identifying ontology paths, a visualization tool to elucidate biological mechanisms of drug responses, and the application of centralized large scale hyperparameter optimization. VETE demonstrated robust accuracy in cancer cell line classification and drug response prediction. Additionally, it provided traceable biological explanations for both tasks and offers insights into the mechanisms underlying its predictions. VETE bridges the gap between AI-driven predictions and biologically meaningful insights in cancer research, which represents a promising advancement in the field.

Estimation of High-Dimensional Markov-Switching VAR Models with an Approximate EM Algorithm

Regime shifts in high-dimensional time series arise naturally in many applications, from neuroimaging to finance. This problem has received considerable attention in low-dimensional settings, with both Bayesian and frequentist methods used extensively for parameter estimation. The EM algorithm is a particularly popular strategy for parameter estimation in low-dimensional settings, although the statistical properties of the resulting estimates have not been well understood. Furthermore, its extension to high-dimensional time series has proved challenging. To overcome these challenges, in this paper we propose an approximate EM algorithm for Markov-switching VAR models that leads to efficient computation and also facilitates the investigation of asymptotic properties of the resulting parameter estimates. We establish the consistency of the proposed EM algorithm in high dimensions and investigate its performance via simulation studies.

Inference on the change point in high dimensional time series models via plug in least squares

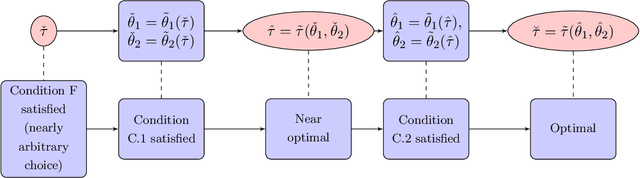
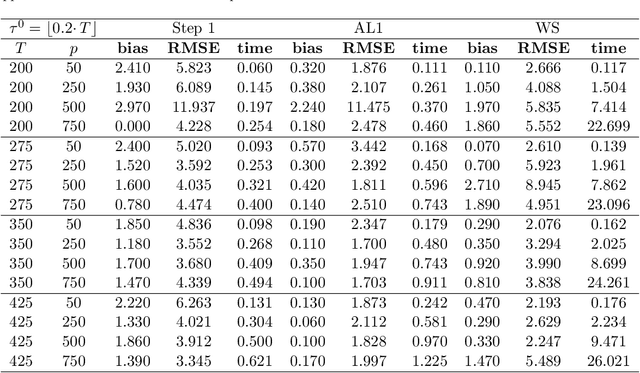
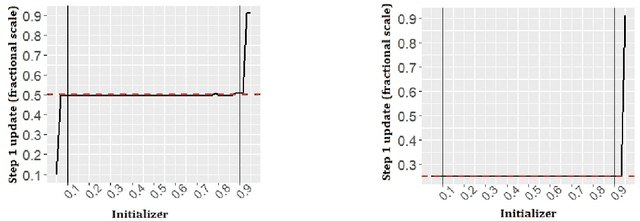
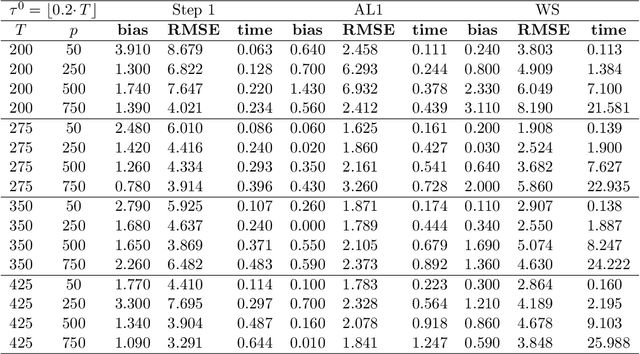
We study a plug in least squares estimator for the change point parameter where change is in the mean of a high dimensional random vector under subgaussian or subexponential distributions. We obtain sufficient conditions under which this estimator possesses sufficient adaptivity against plug in estimates of mean parameters in order to yield an optimal rate of convergence $O_p(\xi^{-2})$ in the integer scale. This rate is preserved while allowing high dimensionality as well as a potentially diminishing jump size $\xi,$ provided $s\log (p\vee T)=o(\surd(Tl_T))$ or $s\log^{3/2}(p\vee T)=o(\surd(Tl_T))$ in the subgaussian and subexponential cases, respectively. Here $s,p,T$ and $l_T$ represent a sparsity parameter, model dimension, sampling period and the separation of the change point from its parametric boundary. Moreover, since the rate of convergence is free of $s,p$ and logarithmic terms of $T,$ it allows the existence of limiting distributions. These distributions are then derived as the {\it argmax} of a two sided negative drift Brownian motion or a two sided negative drift random walk under vanishing and non-vanishing jump size regimes, respectively. Thereby allowing inference of the change point parameter in the high dimensional setting. Feasible algorithms for implementation of the proposed methodology are provided. Theoretical results are supported with monte-carlo simulations.