Nicholas Chia
Division of Data Science and Learning, Argonne National Laboratory, Lemont, IL, USA
HiPerRAG: High-Performance Retrieval Augmented Generation for Scientific Insights
May 07, 2025Abstract:The volume of scientific literature is growing exponentially, leading to underutilized discoveries, duplicated efforts, and limited cross-disciplinary collaboration. Retrieval Augmented Generation (RAG) offers a way to assist scientists by improving the factuality of Large Language Models (LLMs) in processing this influx of information. However, scaling RAG to handle millions of articles introduces significant challenges, including the high computational costs associated with parsing documents and embedding scientific knowledge, as well as the algorithmic complexity of aligning these representations with the nuanced semantics of scientific content. To address these issues, we introduce HiPerRAG, a RAG workflow powered by high performance computing (HPC) to index and retrieve knowledge from more than 3.6 million scientific articles. At its core are Oreo, a high-throughput model for multimodal document parsing, and ColTrast, a query-aware encoder fine-tuning algorithm that enhances retrieval accuracy by using contrastive learning and late-interaction techniques. HiPerRAG delivers robust performance on existing scientific question answering benchmarks and two new benchmarks introduced in this work, achieving 90% accuracy on SciQ and 76% on PubMedQA-outperforming both domain-specific models like PubMedGPT and commercial LLMs such as GPT-4. Scaling to thousands of GPUs on the Polaris, Sunspot, and Frontier supercomputers, HiPerRAG delivers million document-scale RAG workflows for unifying scientific knowledge and fostering interdisciplinary innovation.
AdaParse: An Adaptive Parallel PDF Parsing and Resource Scaling Engine
Apr 23, 2025Abstract:Language models for scientific tasks are trained on text from scientific publications, most distributed as PDFs that require parsing. PDF parsing approaches range from inexpensive heuristics (for simple documents) to computationally intensive ML-driven systems (for complex or degraded ones). The choice of the "best" parser for a particular document depends on its computational cost and the accuracy of its output. To address these issues, we introduce an Adaptive Parallel PDF Parsing and Resource Scaling Engine (AdaParse), a data-driven strategy for assigning an appropriate parser to each document. We enlist scientists to select preferred parser outputs and incorporate this information through direct preference optimization (DPO) into AdaParse, thereby aligning its selection process with human judgment. AdaParse then incorporates hardware requirements and predicted accuracy of each parser to orchestrate computational resources efficiently for large-scale parsing campaigns. We demonstrate that AdaParse, when compared to state-of-the-art parsers, improves throughput by $17\times$ while still achieving comparable accuracy (0.2 percent better) on a benchmark set of 1000 scientific documents. AdaParse's combination of high accuracy and parallel scalability makes it feasible to parse large-scale scientific document corpora to support the development of high-quality, trillion-token-scale text datasets. The implementation is available at https://github.com/7shoe/AdaParse/
Benchmarking community drug response prediction models: datasets, models, tools, and metrics for cross-dataset generalization analysis
Mar 18, 2025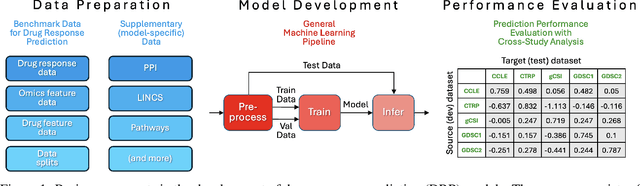
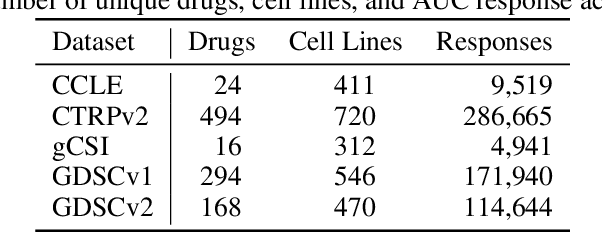
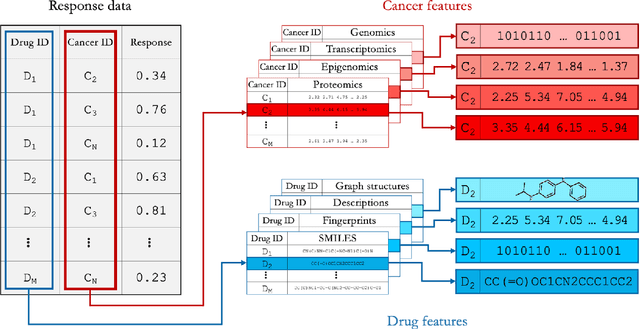

Abstract:Deep learning (DL) and machine learning (ML) models have shown promise in drug response prediction (DRP), yet their ability to generalize across datasets remains an open question, raising concerns about their real-world applicability. Due to the lack of standardized benchmarking approaches, model evaluations and comparisons often rely on inconsistent datasets and evaluation criteria, making it difficult to assess true predictive capabilities. In this work, we introduce a benchmarking framework for evaluating cross-dataset prediction generalization in DRP models. Our framework incorporates five publicly available drug screening datasets, six standardized DRP models, and a scalable workflow for systematic evaluation. To assess model generalization, we introduce a set of evaluation metrics that quantify both absolute performance (e.g., predictive accuracy across datasets) and relative performance (e.g., performance drop compared to within-dataset results), enabling a more comprehensive assessment of model transferability. Our results reveal substantial performance drops when models are tested on unseen datasets, underscoring the importance of rigorous generalization assessments. While several models demonstrate relatively strong cross-dataset generalization, no single model consistently outperforms across all datasets. Furthermore, we identify CTRPv2 as the most effective source dataset for training, yielding higher generalization scores across target datasets. By sharing this standardized evaluation framework with the community, our study aims to establish a rigorous foundation for model comparison, and accelerate the development of robust DRP models for real-world applications.
Variational and Explanatory Neural Networks for Encoding Cancer Profiles and Predicting Drug Responses
Jul 05, 2024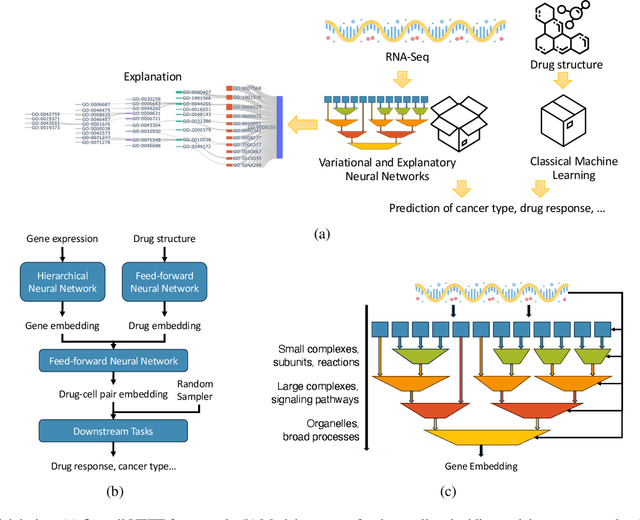

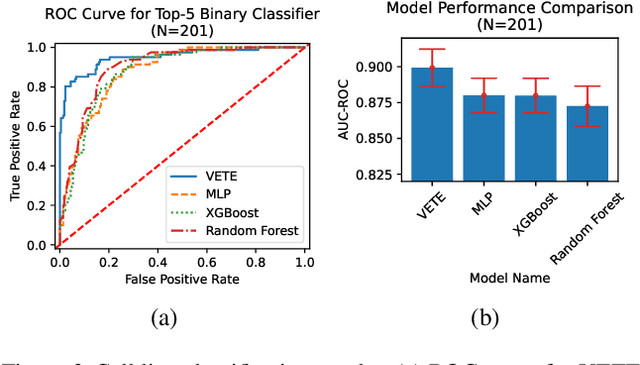
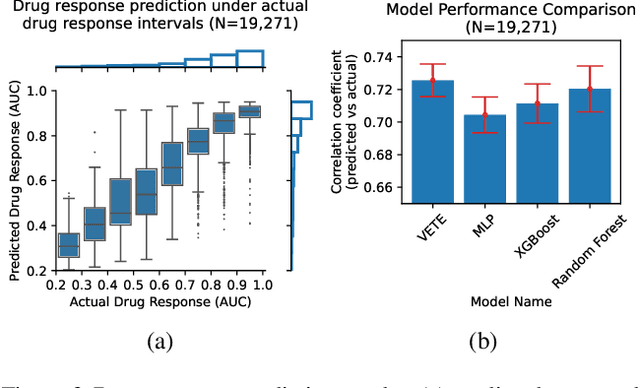
Abstract:Human cancers present a significant public health challenge and require the discovery of novel drugs through translational research. Transcriptomics profiling data that describes molecular activities in tumors and cancer cell lines are widely utilized for predicting anti-cancer drug responses. However, existing AI models face challenges due to noise in transcriptomics data and lack of biological interpretability. To overcome these limitations, we introduce VETE (Variational and Explanatory Transcriptomics Encoder), a novel neural network framework that incorporates a variational component to mitigate noise effects and integrates traceable gene ontology into the neural network architecture for encoding cancer transcriptomics data. Key innovations include a local interpretability-guided method for identifying ontology paths, a visualization tool to elucidate biological mechanisms of drug responses, and the application of centralized large scale hyperparameter optimization. VETE demonstrated robust accuracy in cancer cell line classification and drug response prediction. Additionally, it provided traceable biological explanations for both tasks and offers insights into the mechanisms underlying its predictions. VETE bridges the gap between AI-driven predictions and biologically meaningful insights in cancer research, which represents a promising advancement in the field.
Invariant Risk Minimisation for Cross-Organism Inference: Substituting Mouse Data for Human Data in Human Risk Factor Discovery
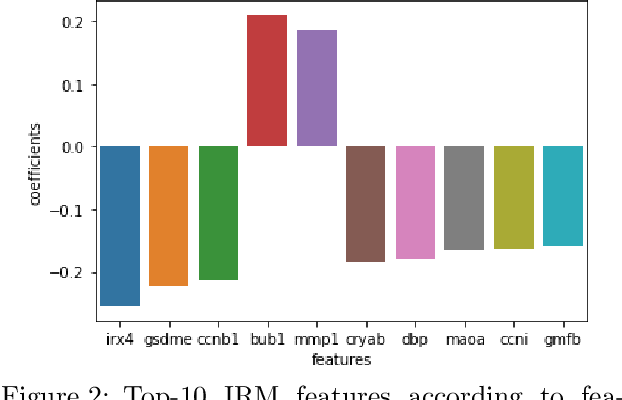
Nov 14, 2021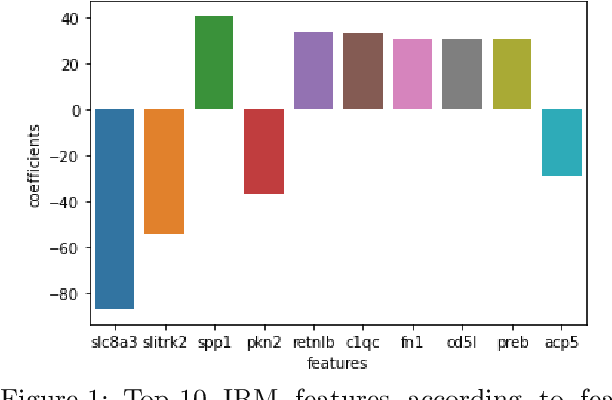
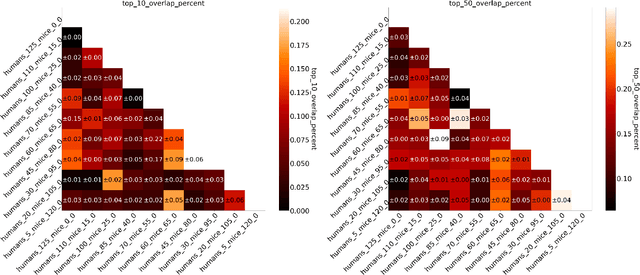
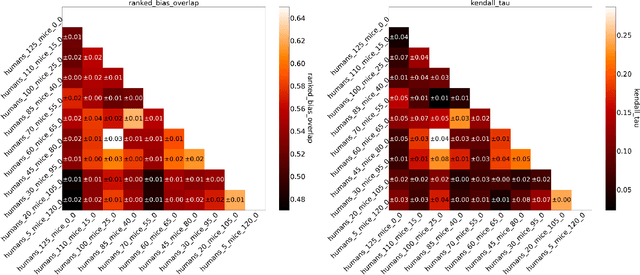
Abstract:Human medical data can be challenging to obtain due to data privacy concerns, difficulties conducting certain types of experiments, or prohibitive associated costs. In many settings, data from animal models or in-vitro cell lines are available to help augment our understanding of human data. However, this data is known for having low etiological validity in comparison to human data. In this work, we augment small human medical datasets with in-vitro data and animal models. We use Invariant Risk Minimisation (IRM) to elucidate invariant features by considering cross-organism data as belonging to different data-generating environments. Our models identify genes of relevance to human cancer development. We observe a degree of consistency between varying the amounts of human and mouse data used, however, further work is required to obtain conclusive insights. As a secondary contribution, we enhance existing open source datasets and provide two uniformly processed, cross-organism, homologue gene-matched datasets to the community.
On Invariance Penalties for Risk Minimization
Jun 17, 2021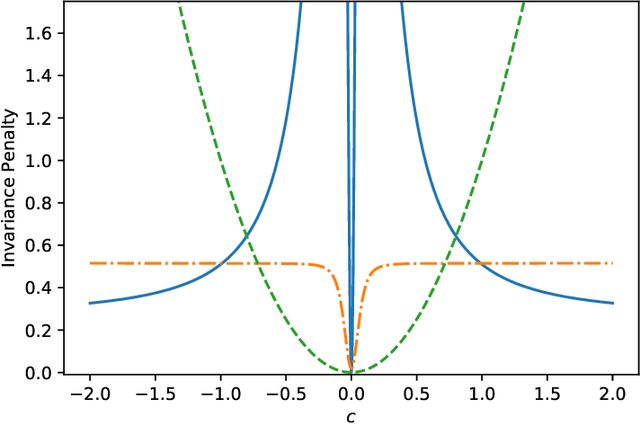
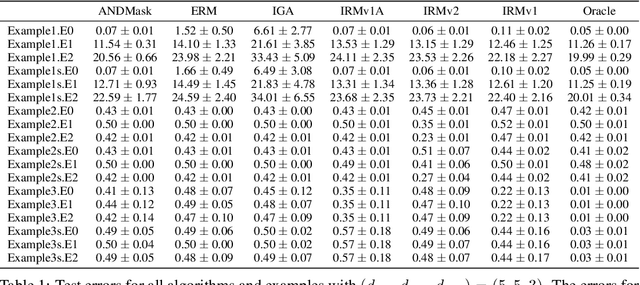

Abstract:The Invariant Risk Minimization (IRM) principle was first proposed by Arjovsky et al. [2019] to address the domain generalization problem by leveraging data heterogeneity from differing experimental conditions. Specifically, IRM seeks to find a data representation under which an optimal classifier remains invariant across all domains. Despite the conceptual appeal of IRM, the effectiveness of the originally proposed invariance penalty has recently been brought into question. In particular, there exists counterexamples for which that invariance penalty can be arbitrarily small for non-invariant data representations. We propose an alternative invariance penalty by revisiting the Gramian matrix of the data representation. We discuss the role of its eigenvalues in the relationship between the risk and the invariance penalty, and demonstrate that it is ill-conditioned for said counterexamples. The proposed approach is guaranteed to recover an invariant representation for linear settings under mild non-degeneracy conditions. Its effectiveness is substantiated by experiments on DomainBed and InvarianceUnitTest, two extensive test beds for domain generalization.
M-decomposability, elliptical unimodal densities, and applications to clustering and kernel density estimation
Apr 21, 2010


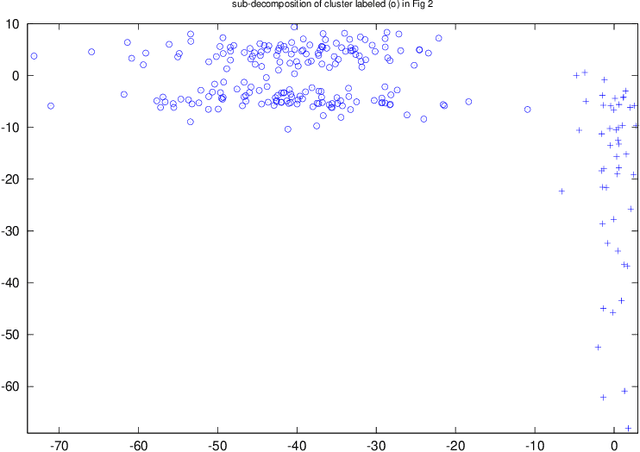
Abstract:Chia and Nakano (2009) introduced the concept of M-decomposability of probability densities in one-dimension. In this paper, we generalize M-decomposability to any dimension. We prove that all elliptical unimodal densities are M-undecomposable. We also derive an inequality to show that it is better to represent an M-decomposable density via a mixture of unimodal densities. Finally, we demonstrate the application of M-decomposability to clustering and kernel density estimation, using real and simulated data. Our results show that M-decomposability can be used as a non-parametric criterion to locate modes in probability densities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge