Inference for Change Points in High Dimensional Mean Shift Models

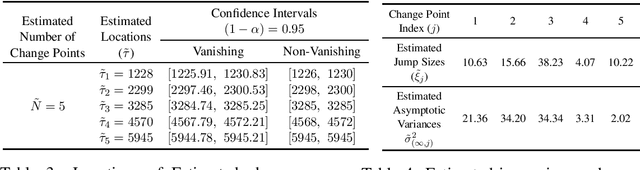
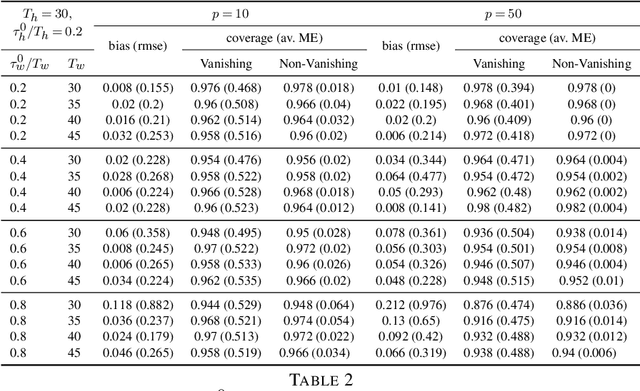
We consider the problem of constructing confidence intervals for the locations of change points in a high-dimensional mean shift model. To that end, we develop a locally refitted least squares estimator and obtain component-wise and simultaneous rates of estimation of the underlying change points. The simultaneous rate is the sharpest available in the literature by at least a factor of $\log p,$ while the component-wise one is optimal. These results enable existence of limiting distributions. Component-wise distributions are characterized under both vanishing and non-vanishing jump size regimes, while joint distributions for any finite subset of change point estimates are characterized under the latter regime, which also yields asymptotic independence of these estimates. The combined results are used to construct asymptotically valid component-wise and simultaneous confidence intervals for the change point parameters. The results are established under a high dimensional scaling, allowing for diminishing jump sizes, in the presence of diverging number of change points and under subexponential errors. They are illustrated on synthetic data and on sensor measurements from smartphones for activity recognition.

Segmentation of high dimensional means over multi-dimensional change points and connections to regression trees

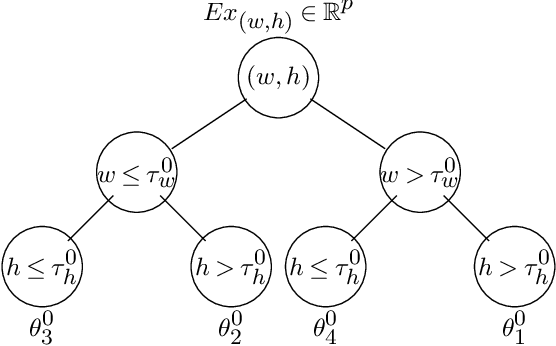
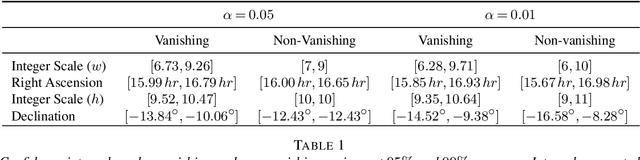
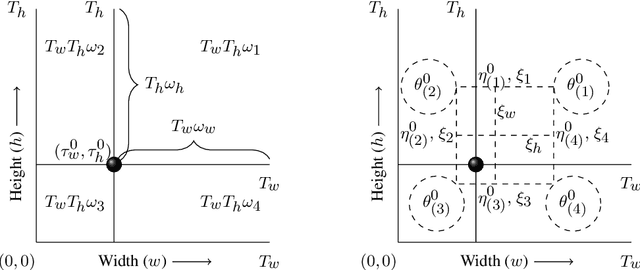
This article is motivated by the objective of providing a new analytically tractable and fully frequentist framework to characterize and implement regression trees while also allowing a multivariate (potentially high dimensional) response. The connection to regression trees is made by a high dimensional model with dynamic mean vectors over multi-dimensional change axes. Our theoretical analysis is carried out under a single two dimensional change point setting. An optimal rate of convergence of the proposed estimator is obtained, which in turn allows existence of limiting distributions. Distributional behavior of change point estimates are split into two distinct regimes, the limiting distributions under each regime is then characterized, in turn allowing construction of asymptotically valid confidence intervals for $2d$-location of change. All results are obtained under a high dimensional scaling $s\log^2 p=o(T_wT_h),$ where $p$ is the response dimension, $s$ is a sparsity parameter, and $T_w,T_h$ are sampling periods along change axes. We characterize full regression trees by defining a multiple multi-dimensional change point model. Natural extensions of the single $2d$-change point estimation methodology are provided. Two applications, first on segmentation of {\it Infra-red astronomy satellite (IRAS)} data and second to segmentation of digital images are provided. Methodology and theoretical results are supported with monte-carlo simulations.

Inference on the change point in high dimensional time series models via plug in least squares

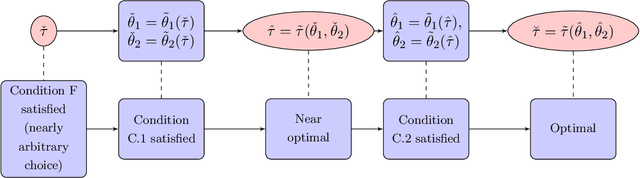
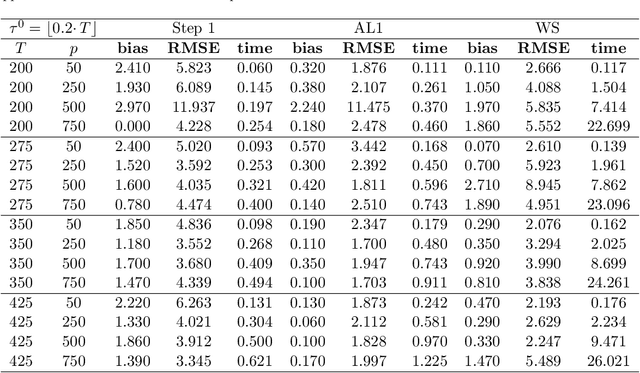
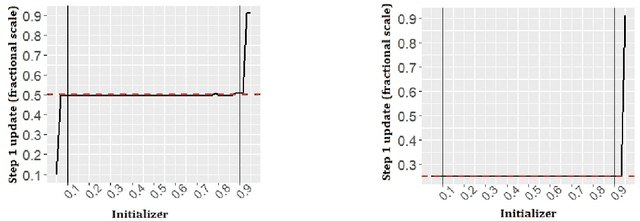
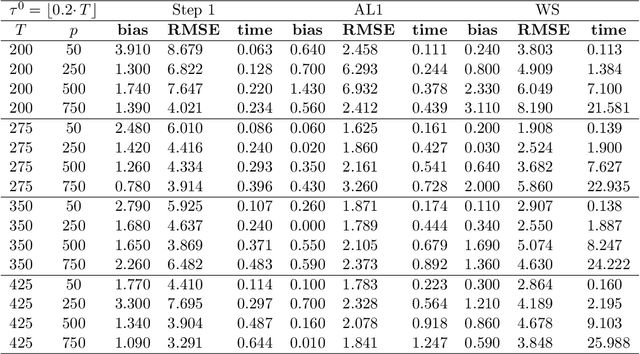
We study a plug in least squares estimator for the change point parameter where change is in the mean of a high dimensional random vector under subgaussian or subexponential distributions. We obtain sufficient conditions under which this estimator possesses sufficient adaptivity against plug in estimates of mean parameters in order to yield an optimal rate of convergence $O_p(\xi^{-2})$ in the integer scale. This rate is preserved while allowing high dimensionality as well as a potentially diminishing jump size $\xi,$ provided $s\log (p\vee T)=o(\surd(Tl_T))$ or $s\log^{3/2}(p\vee T)=o(\surd(Tl_T))$ in the subgaussian and subexponential cases, respectively. Here $s,p,T$ and $l_T$ represent a sparsity parameter, model dimension, sampling period and the separation of the change point from its parametric boundary. Moreover, since the rate of convergence is free of $s,p$ and logarithmic terms of $T,$ it allows the existence of limiting distributions. These distributions are then derived as the {\it argmax} of a two sided negative drift Brownian motion or a two sided negative drift random walk under vanishing and non-vanishing jump size regimes, respectively. Thereby allowing inference of the change point parameter in the high dimensional setting. Feasible algorithms for implementation of the proposed methodology are provided. Theoretical results are supported with monte-carlo simulations.

Inference on the Change Point in High Dimensional Dynamic Graphical Models

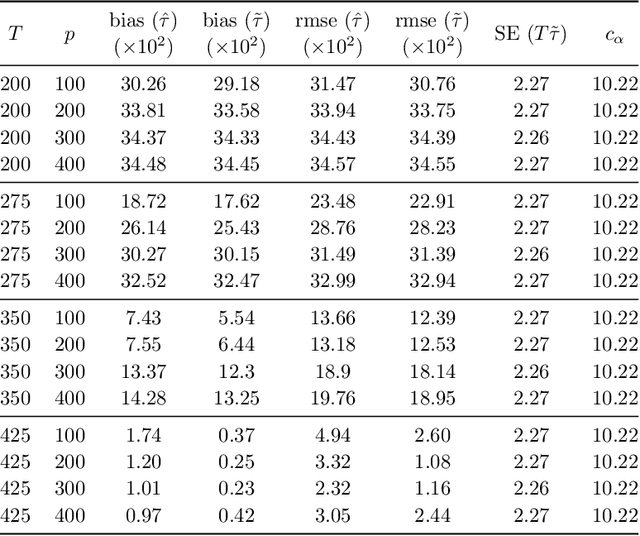
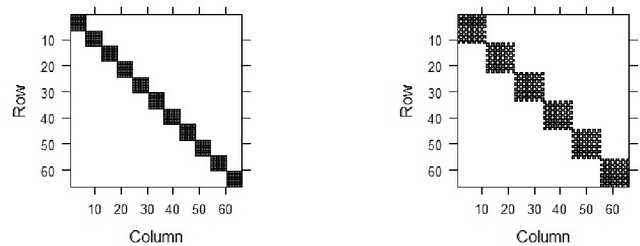
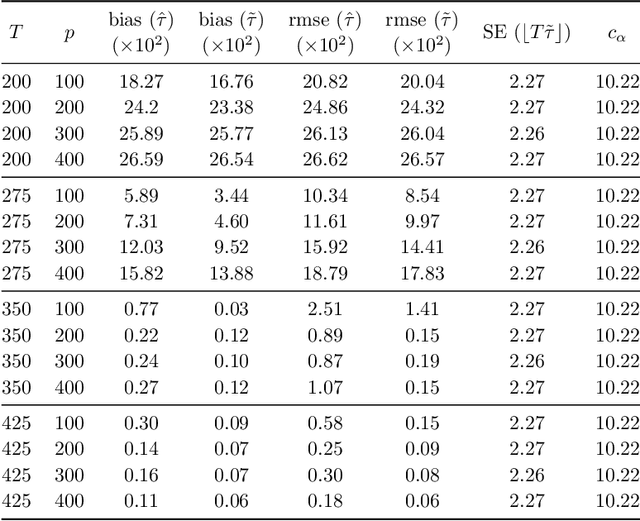
We propose a new estimator for the change point parameter in a dynamic high dimensional graphical model setting. We show that the proposed estimator retains sufficient adaptivity against plugin estimates of the edge structure of the underlying graphical models, in order to yield an $O(\psi^{-2})$ rate of convergence of the change point estimator in the integer scale. This rate is preserved while allowing high dimensionality as well as a diminishing jump size $\psi,$ provided $s\log^{3/2}(p\vee T)=o\big(\surd(Tl_T)\big).$ Here $s,p,T$ and $l_T$ represent a sparsity parameter, model dimension, sampling period and the separation of the change point from its parametric boundary, respectively. Moreover, since the rate of convergence is free of $s,p$ and logarithmic terms of $T,$ it allows the existence of a limiting distribution valid in the high dimensional setting, which is then derived. The method does not assume an underlying Gaussian distribution. Theoretical results are supported numerically with monte carlo simulations.