Hongjin Zhang
Inference on the Change Point in High Dimensional Dynamic Graphical Models
May 19, 2020
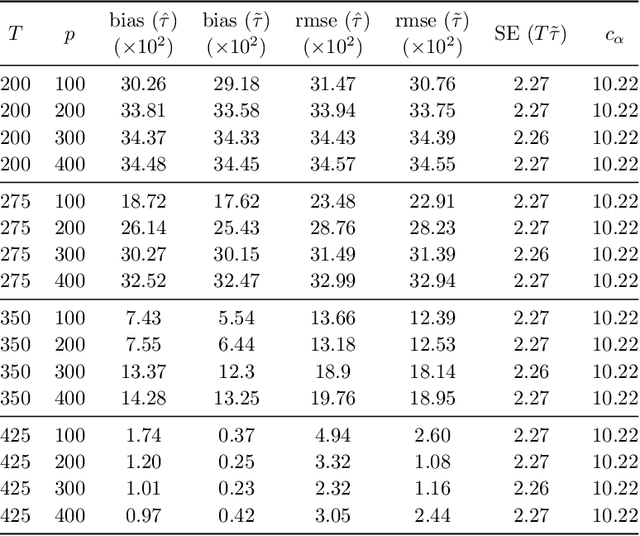
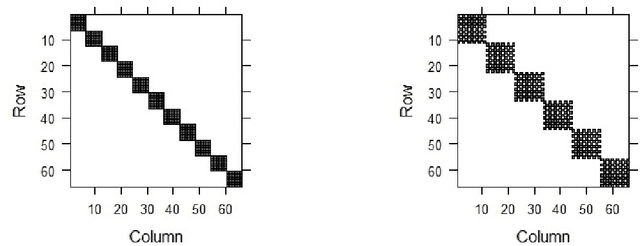
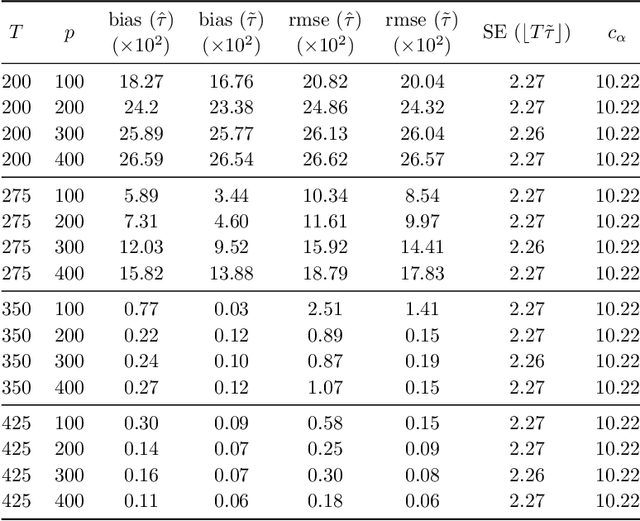
Abstract:We propose a new estimator for the change point parameter in a dynamic high dimensional graphical model setting. We show that the proposed estimator retains sufficient adaptivity against plugin estimates of the edge structure of the underlying graphical models, in order to yield an $O(\psi^{-2})$ rate of convergence of the change point estimator in the integer scale. This rate is preserved while allowing high dimensionality as well as a diminishing jump size $\psi,$ provided $s\log^{3/2}(p\vee T)=o\big(\surd(Tl_T)\big).$ Here $s,p,T$ and $l_T$ represent a sparsity parameter, model dimension, sampling period and the separation of the change point from its parametric boundary, respectively. Moreover, since the rate of convergence is free of $s,p$ and logarithmic terms of $T,$ it allows the existence of a limiting distribution valid in the high dimensional setting, which is then derived. The method does not assume an underlying Gaussian distribution. Theoretical results are supported numerically with monte carlo simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge