The ICME 2025 Audio Encoder Capability Challenge

This challenge aims to evaluate the capabilities of audio encoders, especially in the context of multi-task learning and real-world applications. Participants are invited to submit pre-trained audio encoders that map raw waveforms to continuous embeddings. These encoders will be tested across diverse tasks including speech, environmental sounds, and music, with a focus on real-world usability. The challenge features two tracks: Track A for parameterized evaluation, and Track B for parameter-free evaluation. This challenge provides a platform for evaluating and advancing the state-of-the-art in audio encoder design.

Principal component analysis balancing prediction and approximation accuracy for spatial data

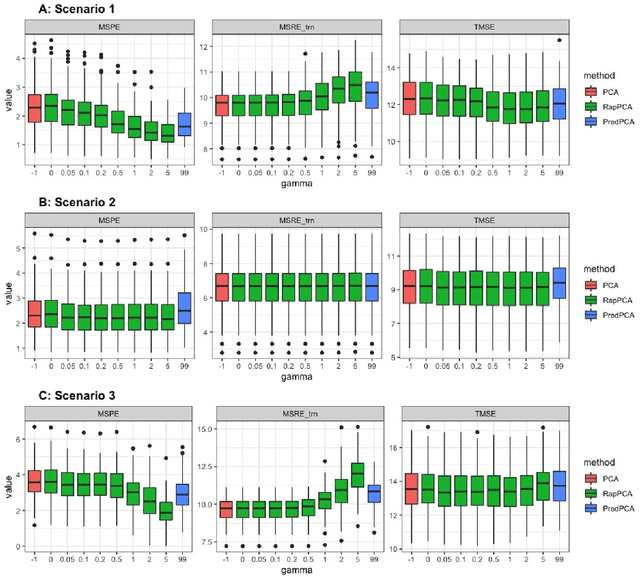
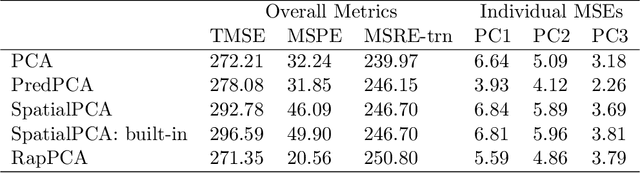
Dimension reduction is often the first step in statistical modeling or prediction of multivariate spatial data. However, most existing dimension reduction techniques do not account for the spatial correlation between observations and do not take the downstream modeling task into consideration when finding the lower-dimensional representation. We formalize the closeness of approximation to the original data and the utility of lower-dimensional scores for downstream modeling as two complementary, sometimes conflicting, metrics for dimension reduction. We illustrate how existing methodologies fall into this framework and propose a flexible dimension reduction algorithm that achieves the optimal trade-off. We derive a computationally simple form for our algorithm and illustrate its performance through simulation studies, as well as two applications in air pollution modeling and spatial transcriptomics.

Variable importance measure for spatial machine learning models with application to air pollution exposure prediction

Exposure assessment is fundamental to air pollution cohort studies. The objective is to predict air pollution exposures for study subjects at locations without data in order to optimize our ability to learn about health effects of air pollution. In addition to generating accurate predictions to minimize exposure measurement error, understanding the mechanism captured by the model is another crucial aspect that may not always be straightforward due to the complex nature of machine learning methods, as well as the lack of unifying notions of variable importance. This is further complicated in air pollution modeling by the presence of spatial correlation. We tackle these challenges in two datasets: sulfur (S) from regulatory United States national PM2.5 sub-species data and ultrafine particles (UFP) from a new Seattle-area traffic-related air pollution dataset. Our key contribution is a leave-one-out approach for variable importance that leads to interpretable and comparable measures for a broad class of models with separable mean and covariance components. We illustrate our approach with several spatial machine learning models, and it clearly highlights the difference in model mechanisms, even for those producing similar predictions. We leverage insights from this variable importance measure to assess the relative utilities of two exposure models for S and UFP that have similar out-of-sample prediction accuracies but appear to draw on different types of spatial information to make predictions.

A Penalized Poisson Likelihood Approach to High-Dimensional Semi-Parametric Inference for Doubly-Stochastic Point Processes

Doubly-stochastic point processes model the occurrence of events over a spatial domain as an inhomogeneous Poisson process conditioned on the realization of a random intensity function. They are flexible tools for capturing spatial heterogeneity and dependence. However, implementations of doubly-stochastic spatial models are computationally demanding, often have limited theoretical guarantee, and/or rely on restrictive assumptions. We propose a penalized regression method for estimating covariate effects in doubly-stochastic point processes that is computationally efficient and does not require a parametric form or stationarity of the underlying intensity. We establish the consistency and asymptotic normality of the proposed estimator, and develop a covariance estimator that leads to a conservative statistical inference procedure. A simulation study shows the validity of our approach under less restrictive assumptions on the data generating mechanism, and an application to Seattle crime data demonstrates better prediction accuracy compared with existing alternatives.