Timothy V. Larson
Principal component analysis balancing prediction and approximation accuracy for spatial data
Aug 03, 2024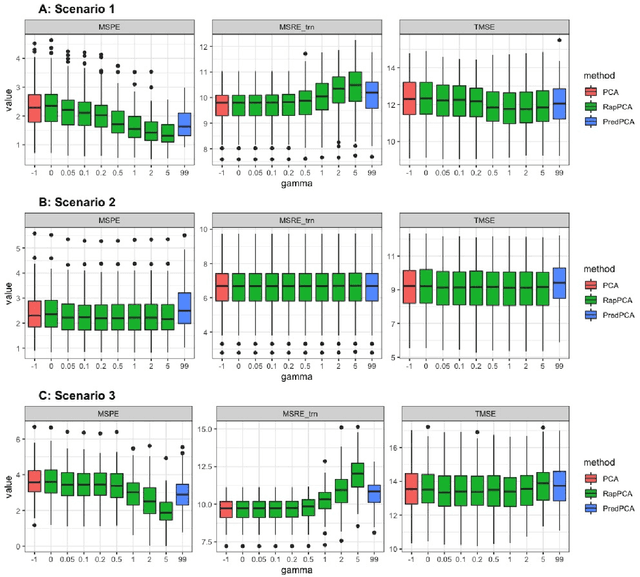


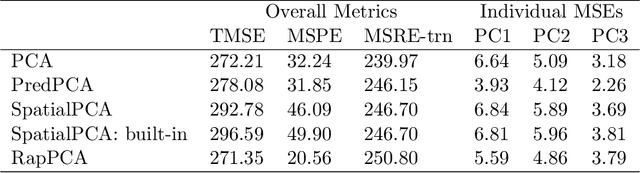
Abstract:Dimension reduction is often the first step in statistical modeling or prediction of multivariate spatial data. However, most existing dimension reduction techniques do not account for the spatial correlation between observations and do not take the downstream modeling task into consideration when finding the lower-dimensional representation. We formalize the closeness of approximation to the original data and the utility of lower-dimensional scores for downstream modeling as two complementary, sometimes conflicting, metrics for dimension reduction. We illustrate how existing methodologies fall into this framework and propose a flexible dimension reduction algorithm that achieves the optimal trade-off. We derive a computationally simple form for our algorithm and illustrate its performance through simulation studies, as well as two applications in air pollution modeling and spatial transcriptomics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge