A Unified Framework for Long Range and Cold Start Forecasting of Seasonal Profiles in Time Series
Paper and Code
Aug 26, 2018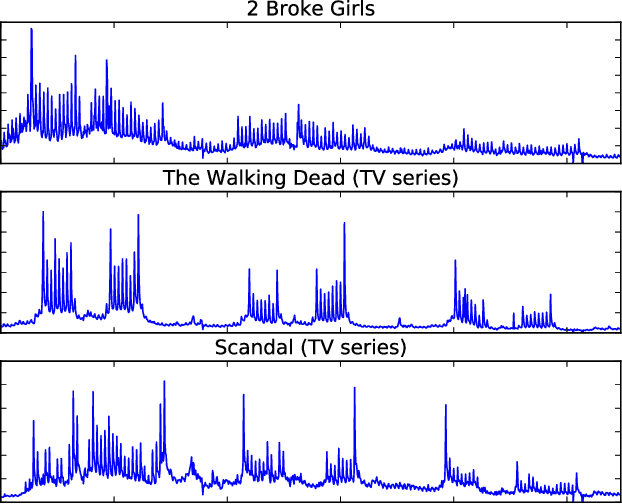
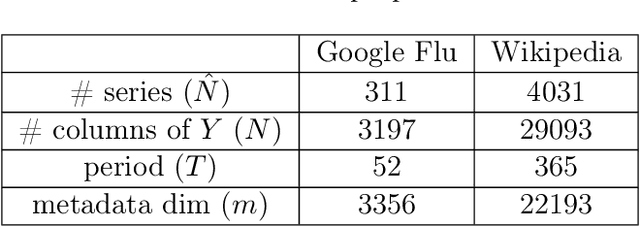
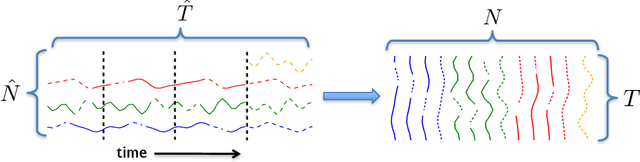
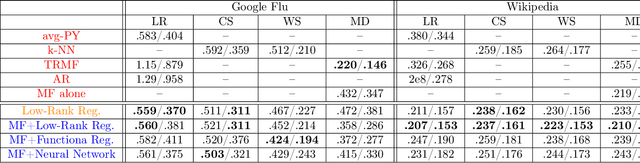
Providing long-range forecasts is a fundamental challenge in time series modeling, which is only compounded by the challenge of having to form such forecasts when a time series has never previously been observed. The latter challenge is the time series version of the cold-start problem seen in recommender systems which, to our knowledge, has not been addressed in previous work. A similar problem occurs when a long range forecast is required after only observing a small number of time points --- a warm start forecast. With these aims in mind, we focus on forecasting seasonal profiles---or baseline demand---for periods on the order of a year in three cases: the long range case with multiple previously observed seasonal profiles, the cold start case with no previous observed seasonal profiles, and the warm start case with only a single partially observed profile. Classical time series approaches that perform iterated step-ahead forecasts based on previous observations struggle to provide accurate long range predictions; in settings with little to no observed data, such approaches are simply not applicable. Instead, we present a straightforward framework which combines ideas from high-dimensional regression and matrix factorization on a carefully constructed data matrix. Key to our formulation and resulting performance is leveraging (1) repeated patterns over fixed periods of time and across series, and (2) metadata associated with the individual series; without this additional data, the cold-start/warm-start problems are nearly impossible to solve. We demonstrate that our framework can accurately forecast an array of seasonal profiles on multiple large scale datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge