Ben Taskar
Expectation-Maximization for Learning Determinantal Point Processes
Nov 04, 2014


Abstract:A determinantal point process (DPP) is a probabilistic model of set diversity compactly parameterized by a positive semi-definite kernel matrix. To fit a DPP to a given task, we would like to learn the entries of its kernel matrix by maximizing the log-likelihood of the available data. However, log-likelihood is non-convex in the entries of the kernel matrix, and this learning problem is conjectured to be NP-hard. Thus, previous work has instead focused on more restricted convex learning settings: learning only a single weight for each row of the kernel matrix, or learning weights for a linear combination of DPPs with fixed kernel matrices. In this work we propose a novel algorithm for learning the full kernel matrix. By changing the kernel parameterization from matrix entries to eigenvalues and eigenvectors, and then lower-bounding the likelihood in the manner of expectation-maximization algorithms, we obtain an effective optimization procedure. We test our method on a real-world product recommendation task, and achieve relative gains of up to 16.5% in test log-likelihood compared to the naive approach of maximizing likelihood by projected gradient ascent on the entries of the kernel matrix.
Learning the Parameters of Determinantal Point Process Kernels
Feb 20, 2014



Abstract:Determinantal point processes (DPPs) are well-suited for modeling repulsion and have proven useful in many applications where diversity is desired. While DPPs have many appealing properties, such as efficient sampling, learning the parameters of a DPP is still considered a difficult problem due to the non-convex nature of the likelihood function. In this paper, we propose using Bayesian methods to learn the DPP kernel parameters. These methods are applicable in large-scale and continuous DPP settings even when the exact form of the eigendecomposition is unknown. We demonstrate the utility of our DPP learning methods in studying the progression of diabetic neuropathy based on spatial distribution of nerve fibers, and in studying human perception of diversity in images.
Controlling Complexity in Part-of-Speech Induction
Jan 16, 2014



Abstract:We consider the problem of fully unsupervised learning of grammatical (part-of-speech) categories from unlabeled text. The standard maximum-likelihood hidden Markov model for this task performs poorly, because of its weak inductive bias and large model capacity. We address this problem by refining the model and modifying the learning objective to control its capacity via para- metric and non-parametric constraints. Our approach enforces word-category association sparsity, adds morphological and orthographic features, and eliminates hard-to-estimate parameters for rare words. We develop an efficient learning algorithm that is not much more computationally intensive than standard training. We also provide an open-source implementation of the algorithm. Our experiments on five diverse languages (Bulgarian, Danish, English, Portuguese, Spanish) achieve significant improvements compared with previous methods for the same task.
Approximate Inference in Continuous Determinantal Point Processes
Nov 12, 2013



Abstract:Determinantal point processes (DPPs) are random point processes well-suited for modeling repulsion. In machine learning, the focus of DPP-based models has been on diverse subset selection from a discrete and finite base set. This discrete setting admits an efficient sampling algorithm based on the eigendecomposition of the defining kernel matrix. Recently, there has been growing interest in using DPPs defined on continuous spaces. While the discrete-DPP sampler extends formally to the continuous case, computationally, the steps required are not tractable in general. In this paper, we present two efficient DPP sampling schemes that apply to a wide range of kernel functions: one based on low rank approximations via Nystrom and random Fourier feature techniques and another based on Gibbs sampling. We demonstrate the utility of continuous DPPs in repulsive mixture modeling and synthesizing human poses spanning activity spaces.
Determinantal point processes for machine learning
Jan 10, 2013



Abstract:Determinantal point processes (DPPs) are elegant probabilistic models of repulsion that arise in quantum physics and random matrix theory. In contrast to traditional structured models like Markov random fields, which become intractable and hard to approximate in the presence of negative correlations, DPPs offer efficient and exact algorithms for sampling, marginalization, conditioning, and other inference tasks. We provide a gentle introduction to DPPs, focusing on the intuitions, algorithms, and extensions that are most relevant to the machine learning community, and show how DPPs can be applied to real-world applications like finding diverse sets of high-quality search results, building informative summaries by selecting diverse sentences from documents, modeling non-overlapping human poses in images or video, and automatically building timelines of important news stories.
* 120 pages
Discriminative Probabilistic Models for Relational Data
Dec 12, 2012



Abstract:In many supervised learning tasks, the entities to be labeled are related to each other in complex ways and their labels are not independent. For example, in hypertext classification, the labels of linked pages are highly correlated. A standard approach is to classify each entity independently, ignoring the correlations between them. Recently, Probabilistic Relational Models, a relational version of Bayesian networks, were used to define a joint probabilistic model for a collection of related entities. In this paper, we present an alternative framework that builds on (conditional) Markov networks and addresses two limitations of the previous approach. First, undirected models do not impose the acyclicity constraint that hinders representation of many important relational dependencies in directed models. Second, undirected models are well suited for discriminative training, where we optimize the conditional likelihood of the labels given the features, which generally improves classification accuracy. We show how to train these models effectively, and how to use approximate probabilistic inference over the learned model for collective classification of multiple related entities. We provide experimental results on a webpage classification task, showing that accuracy can be significantly improved by modeling relational dependencies.
Structured Prediction Cascades
Aug 06, 2012



Abstract:Structured prediction tasks pose a fundamental trade-off between the need for model complexity to increase predictive power and the limited computational resources for inference in the exponentially-sized output spaces such models require. We formulate and develop the Structured Prediction Cascade architecture: a sequence of increasingly complex models that progressively filter the space of possible outputs. The key principle of our approach is that each model in the cascade is optimized to accurately filter and refine the structured output state space of the next model, speeding up both learning and inference in the next layer of the cascade. We learn cascades by optimizing a novel convex loss function that controls the trade-off between the filtering efficiency and the accuracy of the cascade, and provide generalization bounds for both accuracy and efficiency. We also extend our approach to intractable models using tree-decomposition ensembles, and provide algorithms and theory for this setting. We evaluate our approach on several large-scale problems, achieving state-of-the-art performance in handwriting recognition and human pose recognition. We find that structured prediction cascades allow tremendous speedups and the use of previously intractable features and models in both settings.
Mixture-of-Parents Maximum Entropy Markov Models
Jun 20, 2012


Abstract:We present the mixture-of-parents maximum entropy Markov model (MoP-MEMM), a class of directed graphical models extending MEMMs. The MoP-MEMM allows tractable incorporation of long-range dependencies between nodes by restricting the conditional distribution of each node to be a mixture of distributions given the parents. We show how to efficiently compute the exact marginal posterior node distributions, regardless of the range of the dependencies. This enables us to model non-sequential correlations present within text documents, as well as between interconnected documents, such as hyperlinked web pages. We apply the MoP-MEMM to a named entity recognition task and a web page classification task. In each, our model shows significant improvement over the basic MEMM, and is competitive with other long-range sequence models that use approximate inference.
Multi-View Learning over Structured and Non-Identical Outputs
Jun 13, 2012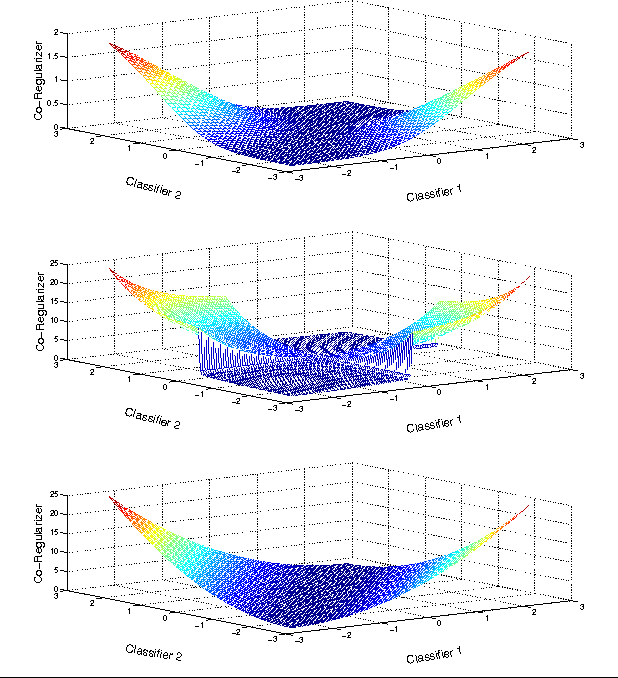
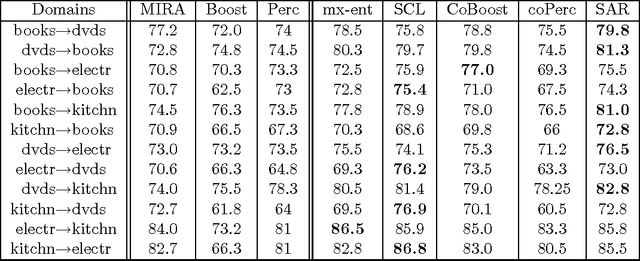
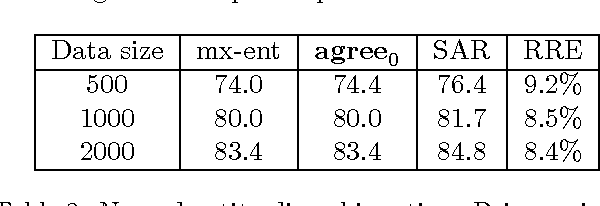
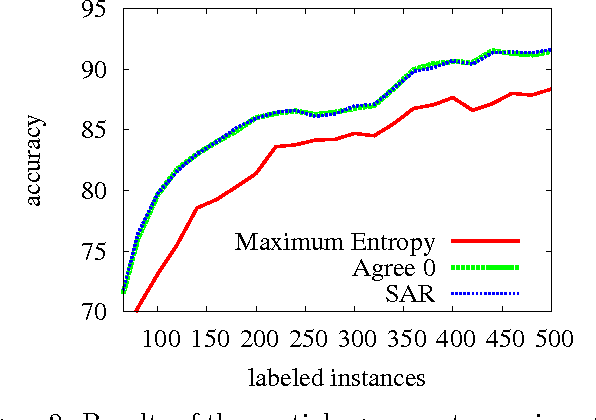
Abstract:In many machine learning problems, labeled training data is limited but unlabeled data is ample. Some of these problems have instances that can be factored into multiple views, each of which is nearly sufficent in determining the correct labels. In this paper we present a new algorithm for probabilistic multi-view learning which uses the idea of stochastic agreement between views as regularization. Our algorithm works on structured and unstructured problems and easily generalizes to partial agreement scenarios. For the full agreement case, our algorithm minimizes the Bhattacharyya distance between the models of each view, and performs better than CoBoosting and two-view Perceptron on several flat and structured classification problems.
Learning Determinantal Point Processes
Feb 14, 2012



Abstract:Determinantal point processes (DPPs), which arise in random matrix theory and quantum physics, are natural models for subset selection problems where diversity is preferred. Among many remarkable properties, DPPs offer tractable algorithms for exact inference, including computing marginal probabilities and sampling; however, an important open question has been how to learn a DPP from labeled training data. In this paper we propose a natural feature-based parameterization of conditional DPPs, and show how it leads to a convex and efficient learning formulation. We analyze the relationship between our model and binary Markov random fields with repulsive potentials, which are qualitatively similar but computationally intractable. Finally, we apply our approach to the task of extractive summarization, where the goal is to choose a small subset of sentences conveying the most important information from a set of documents. In this task there is a fundamental tradeoff between sentences that are highly relevant to the collection as a whole, and sentences that are diverse and not repetitive. Our parameterization allows us to naturally balance these two characteristics. We evaluate our system on data from the DUC 2003/04 multi-document summarization task, achieving state-of-the-art results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge