Query-Adaptive Predictive Inference with Partial Labels

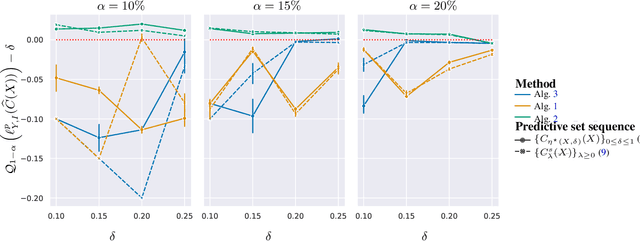
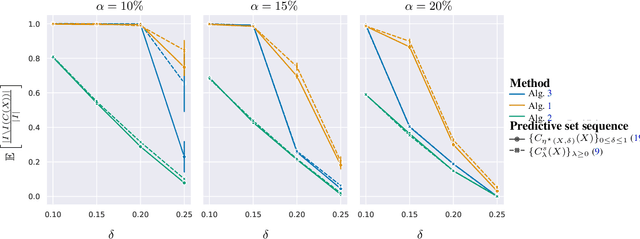
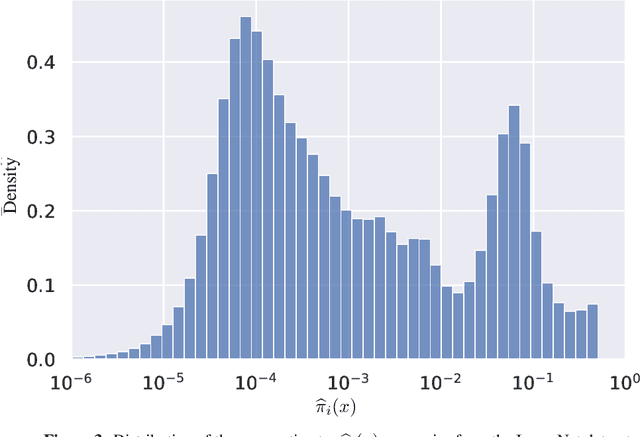
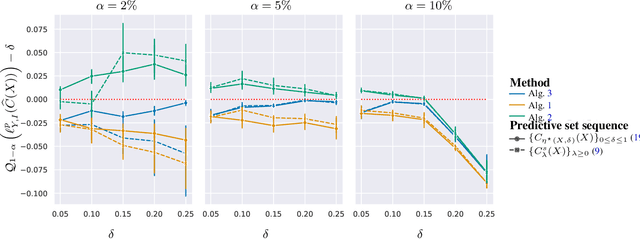
The cost and scarcity of fully supervised labels in statistical machine learning encourage using partially labeled data for model validation as a cheaper and more accessible alternative. Effectively collecting and leveraging weakly supervised data for large-space structured prediction tasks thus becomes an important part of an end-to-end learning system. We propose a new computationally-friendly methodology to construct predictive sets using only partially labeled data on top of black-box predictive models. To do so, we introduce "probe" functions as a way to describe weakly supervised instances and define a false discovery proportion-type loss, both of which seamlessly adapt to partial supervision and structured prediction -- ranking, matching, segmentation, multilabel or multiclass classification. Our experiments highlight the validity of our predictive set construction as well as the attractiveness of a more flexible user-dependent loss framework.

Predictive Inference with Weak Supervision

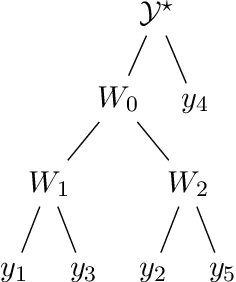
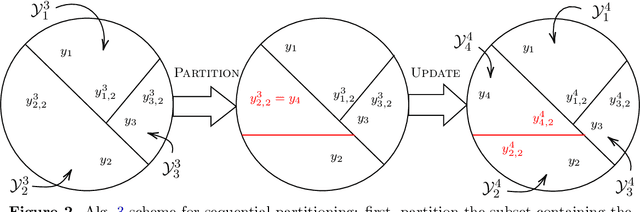
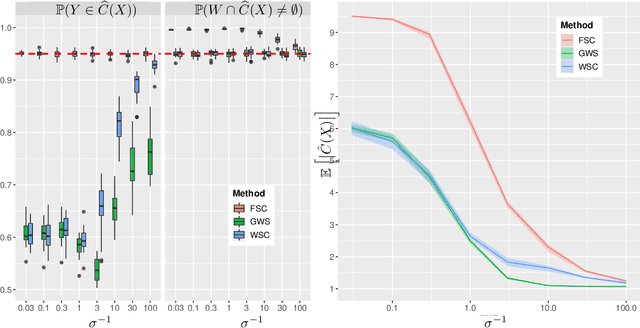
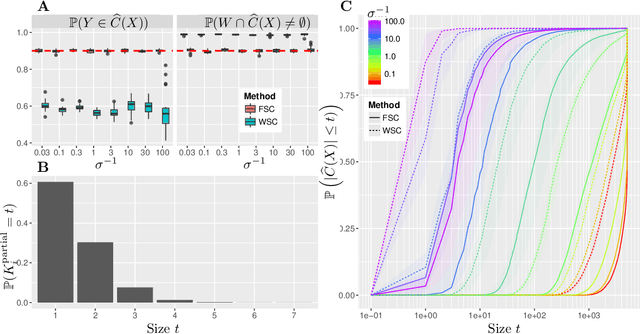
The expense of acquiring labels in large-scale statistical machine learning makes partially and weakly-labeled data attractive, though it is not always apparent how to leverage such data for model fitting or validation. We present a methodology to bridge the gap between partial supervision and validation, developing a conformal prediction framework to provide valid predictive confidence sets -- sets that cover a true label with a prescribed probability, independent of the underlying distribution -- using weakly labeled data. To do so, we introduce a (necessary) new notion of coverage and predictive validity, then develop several application scenarios, providing efficient algorithms for classification and several large-scale structured prediction problems. We corroborate the hypothesis that the new coverage definition allows for tighter and more informative (but valid) confidence sets through several experiments.

The Lifecycle of a Statistical Model: Model Failure Detection, Identification, and Refitting

The statistical machine learning community has demonstrated considerable resourcefulness over the years in developing highly expressive tools for estimation, prediction, and inference. The bedrock assumptions underlying these developments are that the data comes from a fixed population and displays little heterogeneity. But reality is significantly more complex: statistical models now routinely fail when released into real-world systems and scientific applications, where such assumptions rarely hold. Consequently, we pursue a different path in this paper vis-a-vis the well-worn trail of developing new methodology for estimation and prediction. In this paper, we develop tools and theory for detecting and identifying regions of the covariate space (subpopulations) where model performance has begun to degrade, and study intervening to fix these failures through refitting. We present empirical results with three real-world data sets -- including a time series involving forecasting the incidence of COVID-19 -- showing that our methodology generates interpretable results, is useful for tracking model performance, and can boost model performance through refitting. We complement these empirical results with theory proving that our methodology is minimax optimal for recovering anomalous subpopulations as well as refitting to improve accuracy in a structured normal means setting.

Robust Validation: Confident Predictions Even When Distributions Shift

While the traditional viewpoint in machine learning and statistics assumes training and testing samples come from the same population, practice belies this fiction. One strategy---coming from robust statistics and optimization---is thus to build a model robust to distributional perturbations. In this paper, we take a different approach to describe procedures for robust predictive inference, where a model provides uncertainty estimates on its predictions rather than point predictions. We present a method that produces prediction sets (almost exactly) giving the right coverage level for any test distribution in an $f$-divergence ball around the training population. The method, based on conformal inference, achieves (nearly) valid coverage in finite samples, under only the condition that the training data be exchangeable. An essential component of our methodology is to estimate the amount of expected future data shift and build robustness to it; we develop estimators and prove their consistency for protection and validity of uncertainty estimates under shifts. By experimenting on several large-scale benchmark datasets, including Recht et al.'s CIFAR-v4 and ImageNet-V2 datasets, we provide complementary empirical results that highlight the importance of robust predictive validity.

Knowing what you know: valid confidence sets in multiclass and multilabel prediction

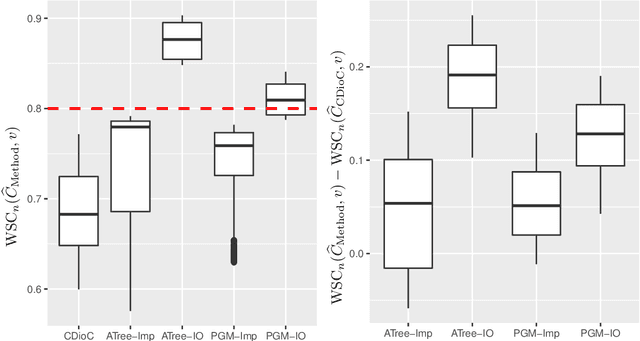
We develop conformal prediction methods for constructing valid predictive confidence sets in multiclass and multilabel problems without assumptions on the data generating distribution. A challenge here is that typical conformal prediction methods---which give marginal validity (coverage) guarantees---provide uneven coverage, in that they address easy examples at the expense of essentially ignoring difficult examples. By leveraging ideas from quantile regression, we build methods that always guarantee correct coverage but additionally provide (asymptotically optimal) conditional coverage for both multiclass and multilabel prediction problems. To address the potential challenge of exponentially large confidence sets in multilabel prediction, we build tree-structured classifiers that efficiently account for interactions between labels. Our methods can be bolted on top of any classification model---neural network, random forest, boosted tree---to guarantee its validity. We also provide an empirical evaluation suggesting the more robust coverage of our confidence sets.