Predictive Inference with Weak Supervision

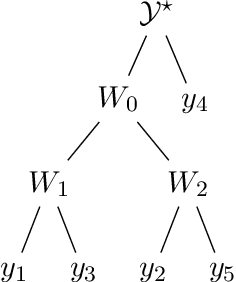
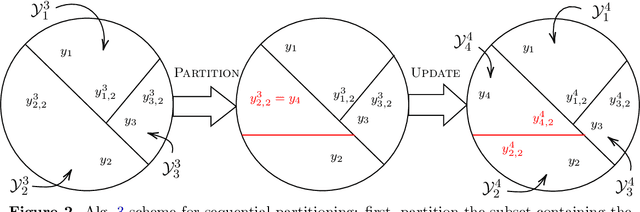
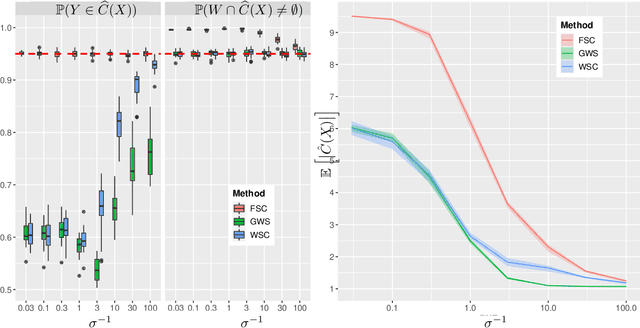
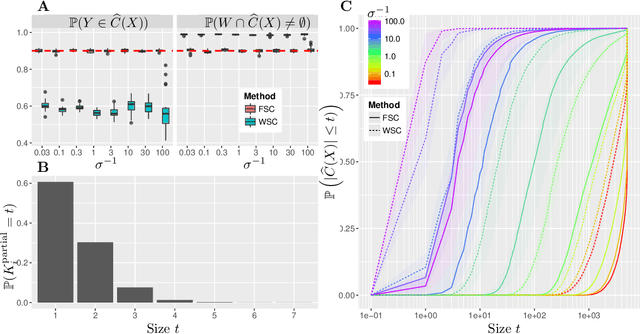
The expense of acquiring labels in large-scale statistical machine learning makes partially and weakly-labeled data attractive, though it is not always apparent how to leverage such data for model fitting or validation. We present a methodology to bridge the gap between partial supervision and validation, developing a conformal prediction framework to provide valid predictive confidence sets -- sets that cover a true label with a prescribed probability, independent of the underlying distribution -- using weakly labeled data. To do so, we introduce a (necessary) new notion of coverage and predictive validity, then develop several application scenarios, providing efficient algorithms for classification and several large-scale structured prediction problems. We corroborate the hypothesis that the new coverage definition allows for tighter and more informative (but valid) confidence sets through several experiments.

The Lifecycle of a Statistical Model: Model Failure Detection, Identification, and Refitting

The statistical machine learning community has demonstrated considerable resourcefulness over the years in developing highly expressive tools for estimation, prediction, and inference. The bedrock assumptions underlying these developments are that the data comes from a fixed population and displays little heterogeneity. But reality is significantly more complex: statistical models now routinely fail when released into real-world systems and scientific applications, where such assumptions rarely hold. Consequently, we pursue a different path in this paper vis-a-vis the well-worn trail of developing new methodology for estimation and prediction. In this paper, we develop tools and theory for detecting and identifying regions of the covariate space (subpopulations) where model performance has begun to degrade, and study intervening to fix these failures through refitting. We present empirical results with three real-world data sets -- including a time series involving forecasting the incidence of COVID-19 -- showing that our methodology generates interpretable results, is useful for tracking model performance, and can boost model performance through refitting. We complement these empirical results with theory proving that our methodology is minimax optimal for recovering anomalous subpopulations as well as refitting to improve accuracy in a structured normal means setting.

Accelerated Gradient Flow: Risk, Stability, and Implicit Regularization

Acceleration and momentum are the de facto standard in modern applications of machine learning and optimization, yet the bulk of the work on implicit regularization focuses instead on unaccelerated methods. In this paper, we study the statistical risk of the iterates generated by Nesterov's accelerated gradient method and Polyak's heavy ball method, when applied to least squares regression, drawing several connections to explicit penalization. We carry out our analyses in continuous-time, allowing us to make sharper statements than in prior work, and revealing complex interactions between early stopping, stability, and the curvature of the loss function.

Minimum-Distortion Embedding

We consider the vector embedding problem. We are given a finite set of items, with the goal of assigning a representative vector to each one, possibly under some constraints (such as the collection of vectors being standardized, i.e., have zero mean and unit covariance). We are given data indicating that some pairs of items are similar, and optionally, some other pairs are dissimilar. For pairs of similar items, we want the corresponding vectors to be near each other, and for dissimilar pairs, we want the corresponding vectors to not be near each other, measured in Euclidean distance. We formalize this by introducing distortion functions, defined for some pairs of the items. Our goal is to choose an embedding that minimizes the total distortion, subject to the constraints. We call this the minimum-distortion embedding (MDE) problem. The MDE framework is simple but general. It includes a wide variety of embedding methods, such as spectral embedding, principal component analysis, multidimensional scaling, dimensionality reduction methods (like Isomap and UMAP), force-directed layout, and others. It also includes new embeddings, and provides principled ways of validating historical and new embeddings alike. We develop a projected quasi-Newton method that approximately solves MDE problems and scales to large data sets. We implement this method in PyMDE, an open-source Python package. In PyMDE, users can select from a library of distortion functions and constraints or specify custom ones, making it easy to rapidly experiment with different embeddings. Our software scales to data sets with millions of items and tens of millions of distortion functions. To demonstrate our method, we compute embeddings for several real-world data sets, including images, an academic co-author network, US county demographic data, and single-cell mRNA transcriptomes.

Robust Validation: Confident Predictions Even When Distributions Shift

While the traditional viewpoint in machine learning and statistics assumes training and testing samples come from the same population, practice belies this fiction. One strategy---coming from robust statistics and optimization---is thus to build a model robust to distributional perturbations. In this paper, we take a different approach to describe procedures for robust predictive inference, where a model provides uncertainty estimates on its predictions rather than point predictions. We present a method that produces prediction sets (almost exactly) giving the right coverage level for any test distribution in an $f$-divergence ball around the training population. The method, based on conformal inference, achieves (nearly) valid coverage in finite samples, under only the condition that the training data be exchangeable. An essential component of our methodology is to estimate the amount of expected future data shift and build robustness to it; we develop estimators and prove their consistency for protection and validity of uncertainty estimates under shifts. By experimenting on several large-scale benchmark datasets, including Recht et al.'s CIFAR-v4 and ImageNet-V2 datasets, we provide complementary empirical results that highlight the importance of robust predictive validity.

The Implicit Regularization of Stochastic Gradient Flow for Least Squares

We study the implicit regularization of mini-batch stochastic gradient descent, when applied to the fundamental problem of least squares regression. We leverage a continuous-time stochastic differential equation having the same moments as stochastic gradient descent, which we call stochastic gradient flow. We give a bound on the excess risk of stochastic gradient flow at time $t$, over ridge regression with tuning parameter $\lambda = 1/t$. The bound may be computed from explicit constants (e.g., the mini-batch size, step size, number of iterations), revealing precisely how these quantities drive the excess risk. Numerical examples show the bound can be small, indicating a tight relationship between the two estimators. We give a similar result relating the coefficients of stochastic gradient flow and ridge. These results hold under no conditions on the data matrix $X$, and across the entire optimization path (not just at convergence).

A Continuous-Time View of Early Stopping for Least Squares Regression

We study the statistical properties of the iterates generated by gradient descent, applied to the fundamental problem of least squares regression. We take a continuous-time view, i.e., consider infinitesimal step sizes in gradient descent, in which case the iterates form a trajectory called gradient flow. In a random matrix theory setup, which allows the number of samples $n$ and features $p$ to diverge in such a way that $p/n \to \gamma \in (0,\infty)$, we derive and analyze an asymptotic risk expression for gradient flow. In particular, we compare the asymptotic risk profile of gradient flow to that of ridge regression. When the feature covariance is spherical, we show that the optimal asymptotic gradient flow risk is between 1 and 1.25 times the optimal asymptotic ridge risk. Further, we derive a calibration between the two risk curves under which the asymptotic gradient flow risk no more than 2.25 times the asymptotic ridge risk, at all points along the path. We present a number of other results illustrating the connections between gradient flow and $\ell_2$ regularization, and numerical experiments that support our theory.

Communication-Avoiding Optimization Methods for Distributed Massive-Scale Sparse Inverse Covariance Estimation

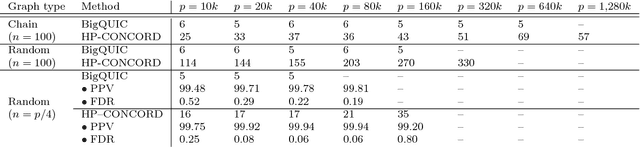
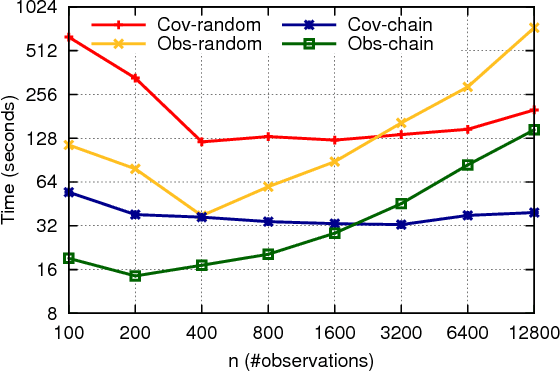
Across a variety of scientific disciplines, sparse inverse covariance estimation is a popular tool for capturing the underlying dependency relationships in multivariate data. Unfortunately, most estimators are not scalable enough to handle the sizes of modern high-dimensional data sets (often on the order of terabytes), and assume Gaussian samples. To address these deficiencies, we introduce HP-CONCORD, a highly scalable optimization method for estimating a sparse inverse covariance matrix based on a regularized pseudolikelihood framework, without assuming Gaussianity. Our parallel proximal gradient method uses a novel communication-avoiding linear algebra algorithm and runs across a multi-node cluster with up to 1k nodes (24k cores), achieving parallel scalability on problems with up to ~819 billion parameters (1.28 million dimensions); even on a single node, HP-CONCORD demonstrates scalability, outperforming a state-of-the-art method. We also use HP-CONCORD to estimate the underlying dependency structure of the brain from fMRI data, and use the result to identify functional regions automatically. The results show good agreement with a clustering from the neuroscience literature.