Penporn Koanantakool
Mesh-TensorFlow: Deep Learning for Supercomputers
Nov 05, 2018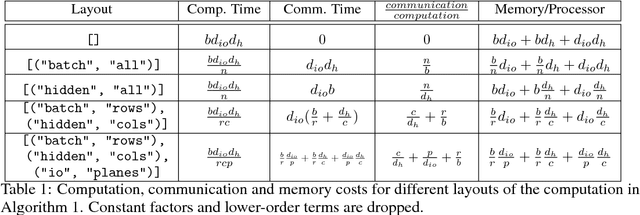
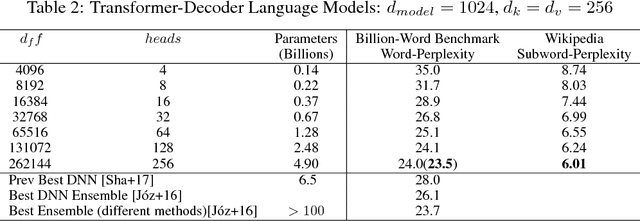
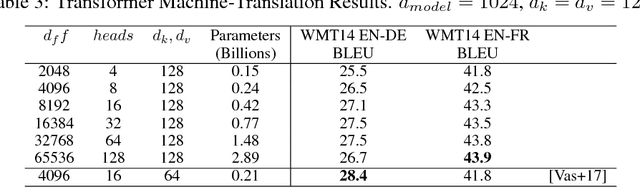
Abstract:Batch-splitting (data-parallelism) is the dominant distributed Deep Neural Network (DNN) training strategy, due to its universal applicability and its amenability to Single-Program-Multiple-Data (SPMD) programming. However, batch-splitting suffers from problems including the inability to train very large models (due to memory constraints), high latency, and inefficiency at small batch sizes. All of these can be solved by more general distribution strategies (model-parallelism). Unfortunately, efficient model-parallel algorithms tend to be complicated to discover, describe, and to implement, particularly on large clusters. We introduce Mesh-TensorFlow, a language for specifying a general class of distributed tensor computations. Where data-parallelism can be viewed as splitting tensors and operations along the "batch" dimension, in Mesh-TensorFlow, the user can specify any tensor-dimensions to be split across any dimensions of a multi-dimensional mesh of processors. A Mesh-TensorFlow graph compiles into a SPMD program consisting of parallel operations coupled with collective communication primitives such as Allreduce. We use Mesh-TensorFlow to implement an efficient data-parallel, model-parallel version of the Transformer sequence-to-sequence model. Using TPU meshes of up to 512 cores, we train Transformer models with up to 5 billion parameters, surpassing state of the art results on WMT'14 English-to-French translation task and the one-billion-word language modeling benchmark. Mesh-Tensorflow is available at https://github.com/tensorflow/mesh .
Communication-Avoiding Optimization Methods for Distributed Massive-Scale Sparse Inverse Covariance Estimation
Apr 08, 2018
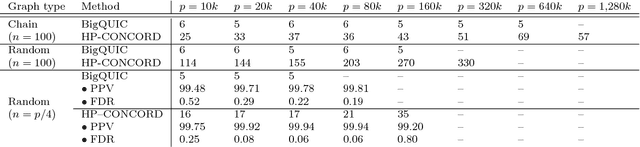

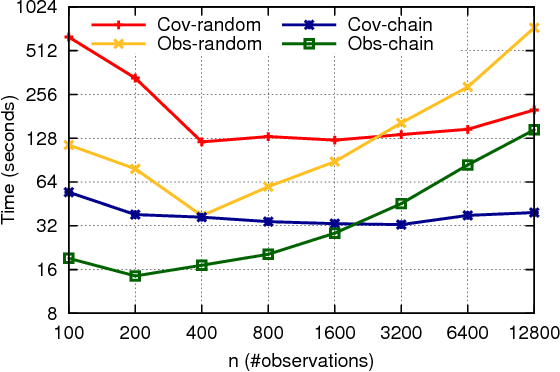
Abstract:Across a variety of scientific disciplines, sparse inverse covariance estimation is a popular tool for capturing the underlying dependency relationships in multivariate data. Unfortunately, most estimators are not scalable enough to handle the sizes of modern high-dimensional data sets (often on the order of terabytes), and assume Gaussian samples. To address these deficiencies, we introduce HP-CONCORD, a highly scalable optimization method for estimating a sparse inverse covariance matrix based on a regularized pseudolikelihood framework, without assuming Gaussianity. Our parallel proximal gradient method uses a novel communication-avoiding linear algebra algorithm and runs across a multi-node cluster with up to 1k nodes (24k cores), achieving parallel scalability on problems with up to ~819 billion parameters (1.28 million dimensions); even on a single node, HP-CONCORD demonstrates scalability, outperforming a state-of-the-art method. We also use HP-CONCORD to estimate the underlying dependency structure of the brain from fMRI data, and use the result to identify functional regions automatically. The results show good agreement with a clustering from the neuroscience literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge