Breaking Boundaries: Distributed Domain Decomposition with Scalable Physics-Informed Neural PDE Solvers

Mosaic Flow is a novel domain decomposition method designed to scale physics-informed neural PDE solvers to large domains. Its unique approach leverages pre-trained networks on small domains to solve partial differential equations on large domains purely through inference, resulting in high reusability. This paper presents an end-to-end parallelization of Mosaic Flow, combining data parallel training and domain parallelism for inference on large-scale problems. By optimizing the network architecture and data parallel training, we significantly reduce the training time for learning the Laplacian operator to minutes on 32 GPUs. Moreover, our distributed domain decomposition algorithm enables scalable inferences for solving the Laplace equation on domains 4096 times larger than the training domain, demonstrating strong scaling while maintaining accuracy on 32 GPUs. The reusability of Mosaic Flow, combined with the improved performance achieved through the distributed-memory algorithms, makes it a promising tool for modeling complex physical phenomena and accelerating scientific discovery.

BubbleML: A Multi-Physics Dataset and Benchmarks for Machine Learning

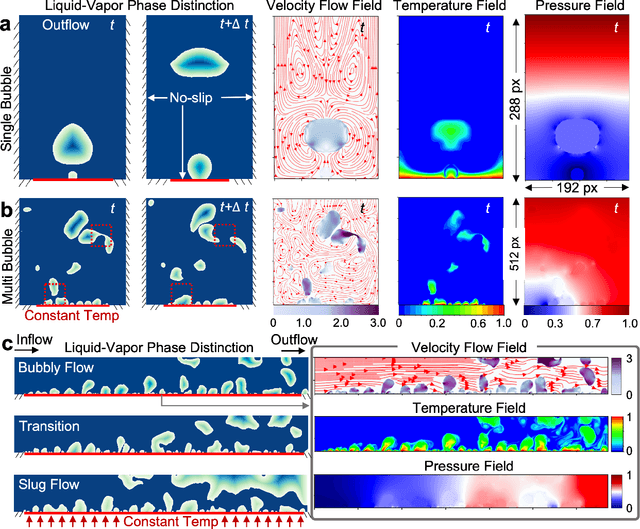
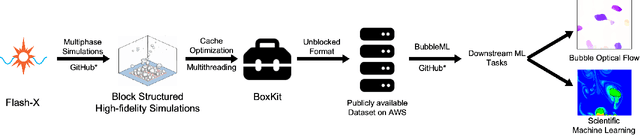
In the field of phase change phenomena, the lack of accessible and diverse datasets suitable for machine learning (ML) training poses a significant challenge. Existing experimental datasets are often restricted, with limited availability and sparse ground truth data, impeding our understanding of this complex multi-physics phenomena. To bridge this gap, we present the BubbleML Dataset(https://github.com/HPCForge/BubbleML) which leverages physics-driven simulations to provide accurate ground truth information for various boiling scenarios, encompassing nucleate pool boiling, flow boiling, and sub-cooled boiling. This extensive dataset covers a wide range of parameters, including varying gravity conditions, flow rates, sub-cooling levels, and wall superheat, comprising 51 simulations. BubbleML is validated against experimental observations and trends, establishing it as an invaluable resource for ML research. Furthermore, we showcase its potential to facilitate exploration of diverse downstream tasks by introducing two benchmarks: (a) optical flow analysis to capture bubble dynamics, and (b) operator networks for learning temperature dynamics. The BubbleML dataset and its benchmarks serve as a catalyst for advancements in ML-driven research on multi-physics phase change phenomena, enabling the development and comparison of state-of-the-art techniques and models.

NUNet: Deep Learning for Non-Uniform Super-Resolution of Turbulent Flows

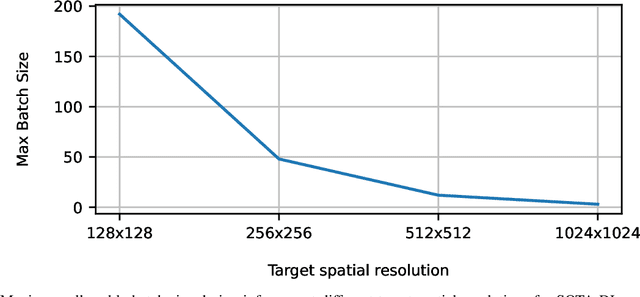
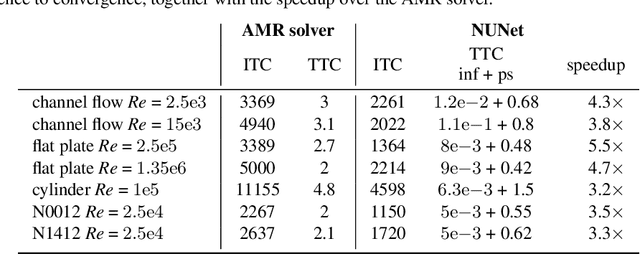
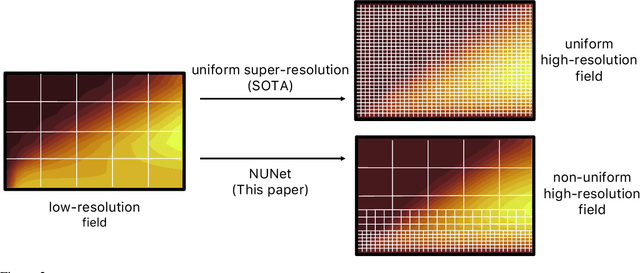
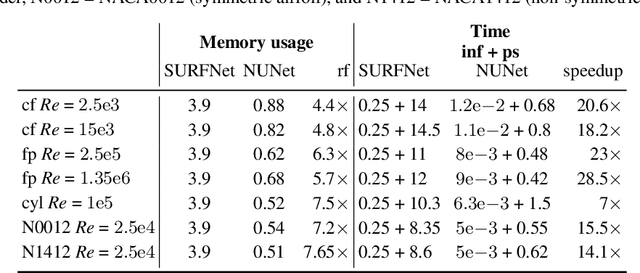
Deep Learning (DL) algorithms are becoming increasingly popular for the reconstruction of high-resolution turbulent flows (aka super-resolution). However, current DL approaches perform spatially uniform super-resolution - a key performance limiter for scalability of DL-based surrogates for Computational Fluid Dynamics (CFD). To address the above challenge, we introduce NUNet, a deep learning-based adaptive mesh refinement (AMR) framework for non-uniform super-resolution of turbulent flows. NUNet divides the input low-resolution flow field into patches, scores each patch, and predicts their target resolution. As a result, it outputs a spatially non-uniform flow field, adaptively refining regions of the fluid domain to achieve the target accuracy. We train NUNet with Reynolds-Averaged Navier-Stokes (RANS) solutions from three different canonical flows, namely turbulent channel flow, flat plate, and flow around ellipses. NUNet shows remarkable discerning properties, refining areas with complex flow features, such as near-wall domains and the wake region in flow around solid bodies, while leaving areas with smooth variations (such as the freestream) in the low-precision range. Hence, NUNet demonstrates an excellent qualitative and quantitative alignment with the traditional OpenFOAM AMR solver. Moreover, it reaches the same convergence guarantees as the AMR solver while accelerating it by 3.2-5.5x, including unseen-during-training geometries and boundary conditions, demonstrating its generalization capacities. Due to NUNet's ability to super-resolve only regions of interest, it predicts the same target 1024x1024 spatial resolution 7-28.5x faster than state-of-the-art DL methods and reduces the memory usage by 4.4-7.65x, showcasing improved scalability.

SURFNet: Super-resolution of Turbulent Flows with Transfer Learning using Small Datasets

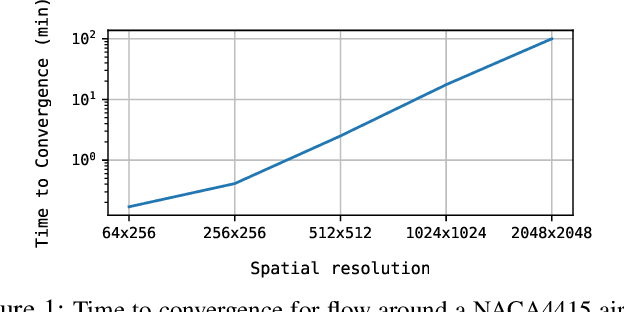
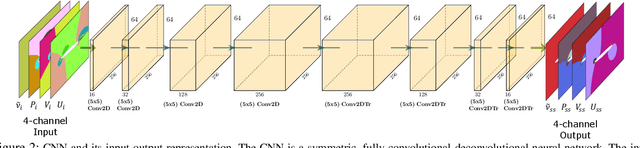
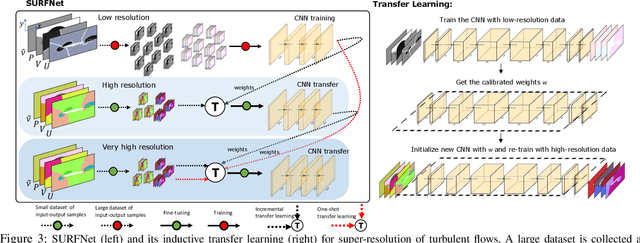
Deep Learning (DL) algorithms are emerging as a key alternative to computationally expensive CFD simulations. However, state-of-the-art DL approaches require large and high-resolution training data to learn accurate models. The size and availability of such datasets are a major limitation for the development of next-generation data-driven surrogate models for turbulent flows. This paper introduces SURFNet, a transfer learning-based super-resolution flow network. SURFNet primarily trains the DL model on low-resolution datasets and transfer learns the model on a handful of high-resolution flow problems - accelerating the traditional numerical solver independent of the input size. We propose two approaches to transfer learning for the task of super-resolution, namely one-shot and incremental learning. Both approaches entail transfer learning on only one geometry to account for fine-grid flow fields requiring 15x less training data on high-resolution inputs compared to the tiny resolution (64x256) of the coarse model, significantly reducing the time for both data collection and training. We empirically evaluate SURFNet's performance by solving the Navier-Stokes equations in the turbulent regime on input resolutions up to 256x larger than the coarse model. On four test geometries and eight flow configurations unseen during training, we observe a consistent 2-2.1x speedup over the OpenFOAM physics solver independent of the test geometry and the resolution size (up to 2048x2048), demonstrating both resolution-invariance and generalization capabilities. Our approach addresses the challenge of reconstructing high-resolution solutions from coarse grid models trained using low-resolution inputs (super-resolution) without loss of accuracy and requiring limited computational resources.

Train Once and Use Forever: Solving Boundary Value Problems in Unseen Domains with Pre-trained Deep Learning Models

Physics-informed neural networks (PINNs) are increasingly employed to replace/augment traditional numerical methods in solving partial differential equations (PDEs). While having many attractive features, state-of-the-art PINNs surrogate a specific realization of a PDE system and hence are problem-specific. That is, each time the boundary conditions and domain shape change, the model needs to be re-trained. This limitation prohibits the application of PINNs in realistic or large-scale engineering problems especially since the costs and efforts associated with their training are considerable. This paper introduces a transferable framework for solving boundary value problems (BVPs) via deep neural networks which can be trained once and used forever for various domains of unseen sizes, shapes, and boundary conditions. First, we introduce \emph{genomic flow network} (GFNet), a neural network that can infer the solution of a BVP across arbitrary boundary conditions on a small square domain called \emph{genome}. Then, we propose \emph{mosaic flow} (MF) predictor, a novel iterative algorithm that assembles or stitches the GFNet's inferences to obtain the solution of BVPs on unseen, large domains while preserving the spatial regularity of the solution. We demonstrate that our framework can estimate the solution of Laplace and Navier-Stokes equations in domains of unseen shapes and boundary conditions that are, respectively, $1200$ and $12$ times larger than the domains where training is performed. Since our framework eliminates the need to re-train, it demonstrates up to 3 orders of magnitude speedups compared to the state-of-the-art.

Brief Announcement: On the Limits of Parallelizing Convolutional Neural Networks on GPUs

GPUs are currently the platform of choice for training neural networks. However, training a deep neural network (DNN) is a time-consuming process even on GPUs because of the massive number of parameters that have to be learned. As a result, accelerating DNN training has been an area of significant research in the last couple of years. While earlier networks such as AlexNet had a linear dependency between layers and operations, state-of-the-art networks such as ResNet, PathNet, and GoogleNet have a non-linear structure that exhibits a higher level of inter-operation parallelism. However, popular deep learning (DL) frameworks such as TensorFlow and PyTorch launch the majority of neural network operations, especially convolutions, serially on GPUs and do not exploit this inter-op parallelism. In this brief announcement, we make a case for the need and potential benefit of exploiting this rich parallelism in state-of-the-art non-linear networks for reducing the training time. We identify the challenges and limitations in enabling concurrent layer execution on GPU backends (such as cuDNN) of DL frameworks and propose potential solutions.

CFDNet: a deep learning-based accelerator for fluid simulations

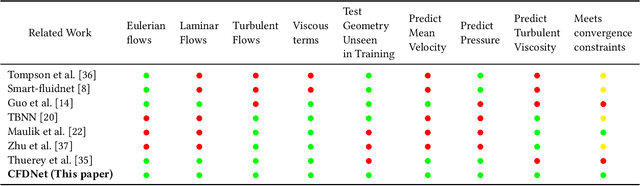
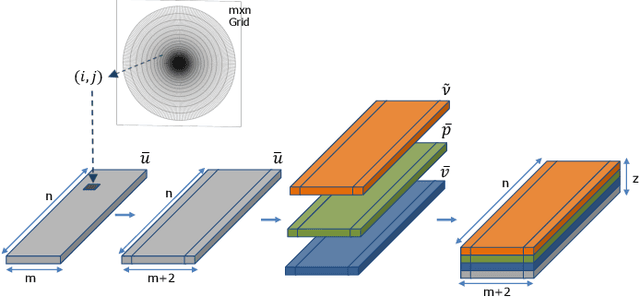
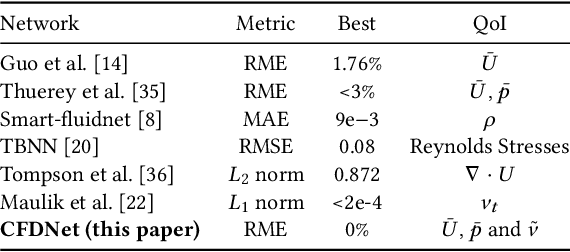
CFD is widely used in physical system design and optimization, where it is used to predict engineering quantities of interest, such as the lift on a plane wing or the drag on a motor vehicle. However, many systems of interest are prohibitively expensive for design optimization, due to the expense of evaluating CFD simulations. To render the computation tractable, reduced-order or surrogate models are used to accelerate simulations while respecting the convergence constraints provided by the higher-fidelity solution. This paper introduces CFDNet -- a physical simulation and deep learning coupled framework, for accelerating the convergence of Reynolds Averaged Navier-Stokes simulations. CFDNet is designed to predict the primary physical properties of the fluid including velocity, pressure, and eddy viscosity using a single convolutional neural network at its core. We evaluate CFDNet on a variety of use-cases, both extrapolative and interpolative, where test geometries are observed/not-observed during training. Our results show that CFDNet meets the convergence constraints of the domain-specific physics solver while outperforming it by 1.9 - 7.4x on both steady laminar and turbulent flows. Moreover, we demonstrate the generalization capacity of CFDNet by testing its prediction on new geometries unseen during training. In this case, the approach meets the CFD convergence criterion while still providing significant speedups over traditional domain-only models.