Breaking Boundaries: Distributed Domain Decomposition with Scalable Physics-Informed Neural PDE Solvers

Mosaic Flow is a novel domain decomposition method designed to scale physics-informed neural PDE solvers to large domains. Its unique approach leverages pre-trained networks on small domains to solve partial differential equations on large domains purely through inference, resulting in high reusability. This paper presents an end-to-end parallelization of Mosaic Flow, combining data parallel training and domain parallelism for inference on large-scale problems. By optimizing the network architecture and data parallel training, we significantly reduce the training time for learning the Laplacian operator to minutes on 32 GPUs. Moreover, our distributed domain decomposition algorithm enables scalable inferences for solving the Laplace equation on domains 4096 times larger than the training domain, demonstrating strong scaling while maintaining accuracy on 32 GPUs. The reusability of Mosaic Flow, combined with the improved performance achieved through the distributed-memory algorithms, makes it a promising tool for modeling complex physical phenomena and accelerating scientific discovery.

BubbleML: A Multi-Physics Dataset and Benchmarks for Machine Learning

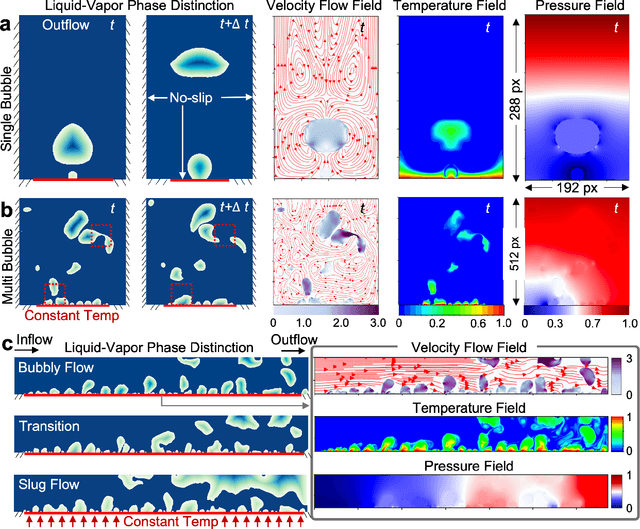
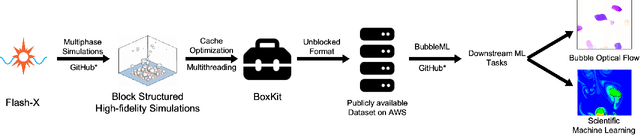
In the field of phase change phenomena, the lack of accessible and diverse datasets suitable for machine learning (ML) training poses a significant challenge. Existing experimental datasets are often restricted, with limited availability and sparse ground truth data, impeding our understanding of this complex multi-physics phenomena. To bridge this gap, we present the BubbleML Dataset(https://github.com/HPCForge/BubbleML) which leverages physics-driven simulations to provide accurate ground truth information for various boiling scenarios, encompassing nucleate pool boiling, flow boiling, and sub-cooled boiling. This extensive dataset covers a wide range of parameters, including varying gravity conditions, flow rates, sub-cooling levels, and wall superheat, comprising 51 simulations. BubbleML is validated against experimental observations and trends, establishing it as an invaluable resource for ML research. Furthermore, we showcase its potential to facilitate exploration of diverse downstream tasks by introducing two benchmarks: (a) optical flow analysis to capture bubble dynamics, and (b) operator networks for learning temperature dynamics. The BubbleML dataset and its benchmarks serve as a catalyst for advancements in ML-driven research on multi-physics phase change phenomena, enabling the development and comparison of state-of-the-art techniques and models.

Relation Matters in Sampling: A Scalable Multi-Relational Graph Neural Network for Drug-Drug Interaction Prediction

Sampling is an established technique to scale graph neural networks to large graphs. Current approaches however assume the graphs to be homogeneous in terms of relations and ignore relation types, critically important in biomedical graphs. Multi-relational graphs contain various types of relations that usually come with variable frequency and have different importance for the problem at hand. We propose an approach to modeling the importance of relation types for neighborhood sampling in graph neural networks and show that we can learn the right balance: relation-type probabilities that reflect both frequency and importance. Our experiments on drug-drug interaction prediction show that state-of-the-art graph neural networks profit from relation-dependent sampling in terms of both accuracy and efficiency.