Scheduling with Speed Predictions
Paper and Code
May 02, 2022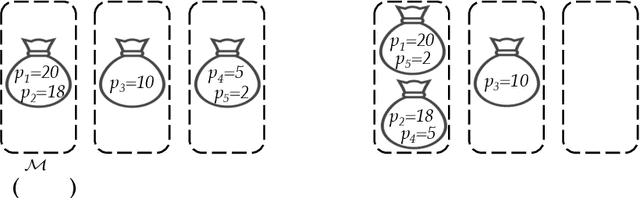
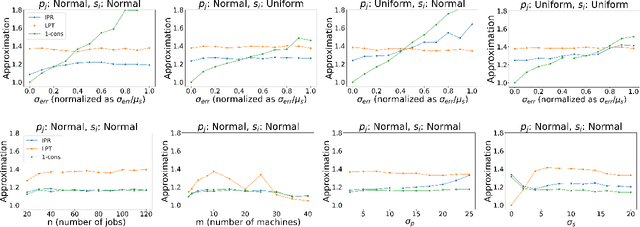
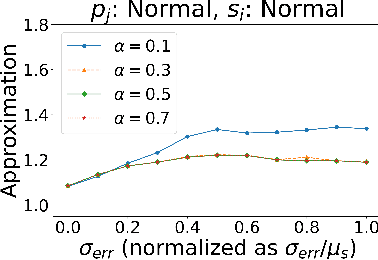
Algorithms with predictions is a recent framework that has been used to overcome pessimistic worst-case bounds in incomplete information settings. In the context of scheduling, very recent work has leveraged machine-learned predictions to design algorithms that achieve improved approximation ratios in settings where the processing times of the jobs are initially unknown. In this paper, we study the speed-robust scheduling problem where the speeds of the machines, instead of the processing times of the jobs, are unknown and augment this problem with predictions. Our main result is an algorithm that achieves a $\min\{\eta^2(1+\epsilon)^2(1+\alpha), (1+\epsilon)(2 + 2/\alpha)\}$ approximation, for any constants $\alpha, \epsilon \in (0,1)$, where $\eta \geq 1$ is the prediction error. When the predictions are accurate, this approximation improves over the previously best known approximation of $2-1/m$ for speed-robust scheduling, where $m$ is the number of machines, while simultaneously maintaining a worst-case approximation of $(1+\epsilon)(2 + 2/\alpha)$ even when the predictions are wrong. In addition, we obtain improved approximations for the special cases of equal and infinitesimal job sizes, and we complement our algorithmic results with lower bounds. Finally, we empirically evaluate our algorithm against existing algorithms for speed-robust scheduling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge