Hao-Ting Wei
Energy-Efficient Scheduling with Predictions
Feb 27, 2024Abstract:An important goal of modern scheduling systems is to efficiently manage power usage. In energy-efficient scheduling, the operating system controls the speed at which a machine is processing jobs with the dual objective of minimizing energy consumption and optimizing the quality of service cost of the resulting schedule. Since machine-learned predictions about future requests can often be learned from historical data, a recent line of work on learning-augmented algorithms aims to achieve improved performance guarantees by leveraging predictions. In particular, for energy-efficient scheduling, Bamas et. al. [BamasMRS20] and Antoniadis et. al. [antoniadis2021novel] designed algorithms with predictions for the energy minimization with deadlines problem and achieved an improved competitive ratio when the prediction error is small while also maintaining worst-case bounds even when the prediction error is arbitrarily large. In this paper, we consider a general setting for energy-efficient scheduling and provide a flexible learning-augmented algorithmic framework that takes as input an offline and an online algorithm for the desired energy-efficient scheduling problem. We show that, when the prediction error is small, this framework gives improved competitive ratios for many different energy-efficient scheduling problems, including energy minimization with deadlines, while also maintaining a bounded competitive ratio regardless of the prediction error. Finally, we empirically demonstrate that this framework achieves an improved performance on real and synthetic datasets.
Learning-Augmented Online Packet Scheduling with Deadlines
May 11, 2023Abstract:The modern network aims to prioritize critical traffic over non-critical traffic and effectively manage traffic flow. This necessitates proper buffer management to prevent the loss of crucial traffic while minimizing the impact on non-critical traffic. Therefore, the algorithm's objective is to control which packets to transmit and which to discard at each step. In this study, we initiate the learning-augmented online packet scheduling with deadlines and provide a novel algorithmic framework to cope with the prediction. We show that when the prediction error is small, our algorithm improves the competitive ratio while still maintaining a bounded competitive ratio, regardless of the prediction error.
Online TSP with Predictions
Jun 30, 2022Abstract:We initiate the study of online routing problems with predictions, inspired by recent exciting results in the area of learning-augmented algorithms. A learning-augmented online algorithm which incorporates predictions in a black-box manner to outperform existing algorithms if the predictions are accurate while otherwise maintaining theoretical guarantees even when the predictions are extremely erroneous is a popular framework for overcoming pessimistic worst-case competitive analysis. In this study, we particularly begin investigating the classical online traveling salesman problem (OLTSP), where future requests are augmented with predictions. Unlike the prediction models in other previous studies, each actual request in the OLTSP, associated with its arrival time and position, may not coincide with the predicted ones, which, as imagined, leads to a troublesome situation. Our main result is to study different prediction models and design algorithms to improve the best-known results in the different settings. Moreover, we generalize the proposed results to the online dial-a-ride problem.
Scheduling with Speed Predictions
May 02, 2022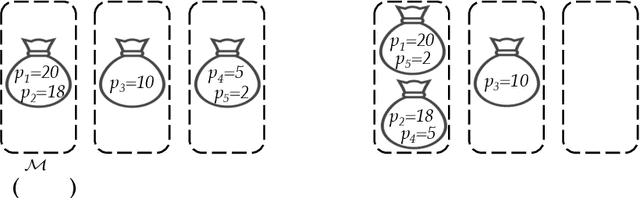
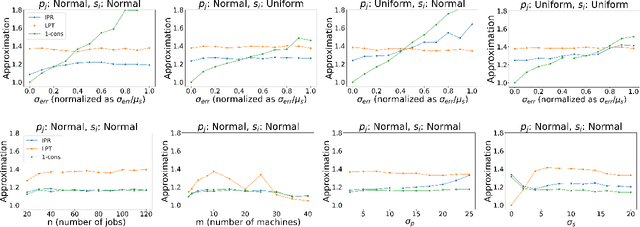
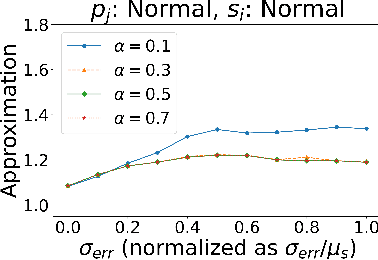
Abstract:Algorithms with predictions is a recent framework that has been used to overcome pessimistic worst-case bounds in incomplete information settings. In the context of scheduling, very recent work has leveraged machine-learned predictions to design algorithms that achieve improved approximation ratios in settings where the processing times of the jobs are initially unknown. In this paper, we study the speed-robust scheduling problem where the speeds of the machines, instead of the processing times of the jobs, are unknown and augment this problem with predictions. Our main result is an algorithm that achieves a $\min\{\eta^2(1+\epsilon)^2(1+\alpha), (1+\epsilon)(2 + 2/\alpha)\}$ approximation, for any constants $\alpha, \epsilon \in (0,1)$, where $\eta \geq 1$ is the prediction error. When the predictions are accurate, this approximation improves over the previously best known approximation of $2-1/m$ for speed-robust scheduling, where $m$ is the number of machines, while simultaneously maintaining a worst-case approximation of $(1+\epsilon)(2 + 2/\alpha)$ even when the predictions are wrong. In addition, we obtain improved approximations for the special cases of equal and infinitesimal job sizes, and we complement our algorithmic results with lower bounds. Finally, we empirically evaluate our algorithm against existing algorithms for speed-robust scheduling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge