Fair Secretaries with Unfair Predictions

Algorithms with predictions is a recent framework for decision-making under uncertainty that leverages the power of machine-learned predictions without making any assumption about their quality. The goal in this framework is for algorithms to achieve an improved performance when the predictions are accurate while maintaining acceptable guarantees when the predictions are erroneous. A serious concern with algorithms that use predictions is that these predictions can be biased and, as a result, cause the algorithm to make decisions that are deemed unfair. We show that this concern manifests itself in the classical secretary problem in the learning-augmented setting -- the state-of-the-art algorithm can have zero probability of accepting the best candidate, which we deem unfair, despite promising to accept a candidate whose expected value is at least $\max\{\Omega (1) , 1 - O(\epsilon)\}$ times the optimal value, where $\epsilon$ is the prediction error. We show how to preserve this promise while also guaranteeing to accept the best candidate with probability $\Omega(1)$. Our algorithm and analysis are based on a new "pegging" idea that diverges from existing works and simplifies/unifies some of their results. Finally, we extend to the $k$-secretary problem and complement our theoretical analysis with experiments.

Energy-Efficient Scheduling with Predictions

An important goal of modern scheduling systems is to efficiently manage power usage. In energy-efficient scheduling, the operating system controls the speed at which a machine is processing jobs with the dual objective of minimizing energy consumption and optimizing the quality of service cost of the resulting schedule. Since machine-learned predictions about future requests can often be learned from historical data, a recent line of work on learning-augmented algorithms aims to achieve improved performance guarantees by leveraging predictions. In particular, for energy-efficient scheduling, Bamas et. al. [BamasMRS20] and Antoniadis et. al. [antoniadis2021novel] designed algorithms with predictions for the energy minimization with deadlines problem and achieved an improved competitive ratio when the prediction error is small while also maintaining worst-case bounds even when the prediction error is arbitrarily large. In this paper, we consider a general setting for energy-efficient scheduling and provide a flexible learning-augmented algorithmic framework that takes as input an offline and an online algorithm for the desired energy-efficient scheduling problem. We show that, when the prediction error is small, this framework gives improved competitive ratios for many different energy-efficient scheduling problems, including energy minimization with deadlines, while also maintaining a bounded competitive ratio regardless of the prediction error. Finally, we empirically demonstrate that this framework achieves an improved performance on real and synthetic datasets.

Scheduling with Speed Predictions

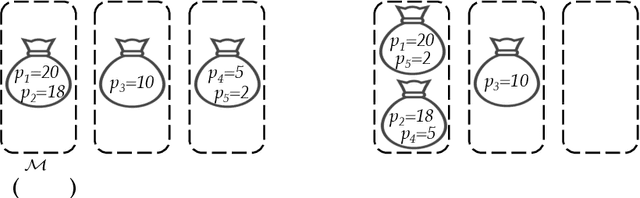
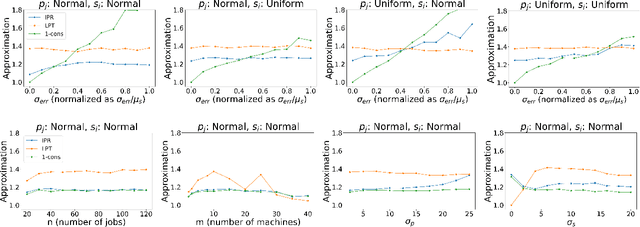
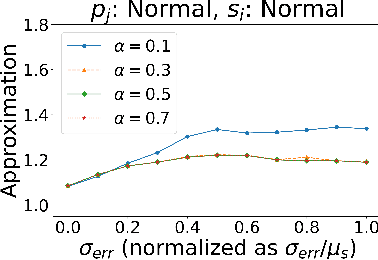
Algorithms with predictions is a recent framework that has been used to overcome pessimistic worst-case bounds in incomplete information settings. In the context of scheduling, very recent work has leveraged machine-learned predictions to design algorithms that achieve improved approximation ratios in settings where the processing times of the jobs are initially unknown. In this paper, we study the speed-robust scheduling problem where the speeds of the machines, instead of the processing times of the jobs, are unknown and augment this problem with predictions. Our main result is an algorithm that achieves a $\min\{\eta^2(1+\epsilon)^2(1+\alpha), (1+\epsilon)(2 + 2/\alpha)\}$ approximation, for any constants $\alpha, \epsilon \in (0,1)$, where $\eta \geq 1$ is the prediction error. When the predictions are accurate, this approximation improves over the previously best known approximation of $2-1/m$ for speed-robust scheduling, where $m$ is the number of machines, while simultaneously maintaining a worst-case approximation of $(1+\epsilon)(2 + 2/\alpha)$ even when the predictions are wrong. In addition, we obtain improved approximations for the special cases of equal and infinitesimal job sizes, and we complement our algorithmic results with lower bounds. Finally, we empirically evaluate our algorithm against existing algorithms for speed-robust scheduling.

Learning Low Degree Hypergraphs

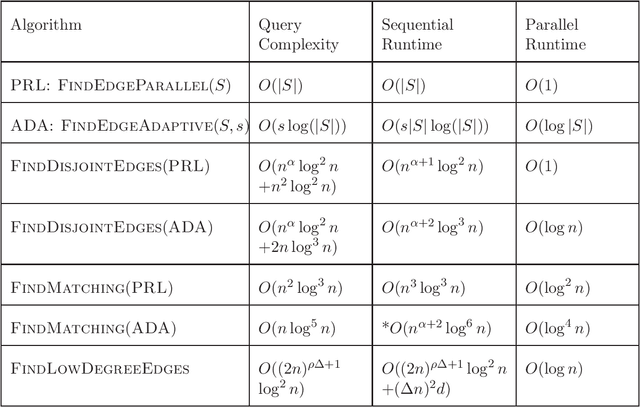
We study the problem of learning a hypergraph via edge detecting queries. In this problem, a learner queries subsets of vertices of a hidden hypergraph and observes whether these subsets contain an edge or not. In general, learning a hypergraph with $m$ edges of maximum size $d$ requires $\Omega((2m/d)^{d/2})$ queries. In this paper, we aim to identify families of hypergraphs that can be learned without suffering from a query complexity that grows exponentially in the size of the edges. We show that hypermatchings and low-degree near-uniform hypergraphs with $n$ vertices are learnable with poly$(n)$ queries. For learning hypermatchings (hypergraphs of maximum degree $ 1$), we give an $O(\log^3 n)$-round algorithm with $O(n \log^5 n)$ queries. We complement this upper bound by showing that there are no algorithms with poly$(n)$ queries that learn hypermatchings in $o(\log \log n)$ adaptive rounds. For hypergraphs with maximum degree $\Delta$ and edge size ratio $\rho$, we give a non-adaptive algorithm with $O((2n)^{\rho \Delta+1}\log^2 n)$ queries. To the best of our knowledge, these are the first algorithms with poly$(n, m)$ query complexity for learning non-trivial families of hypergraphs that have a super-constant number of edges of super-constant size.

Instance Specific Approximations for Submodular Maximization

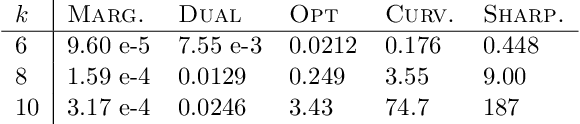
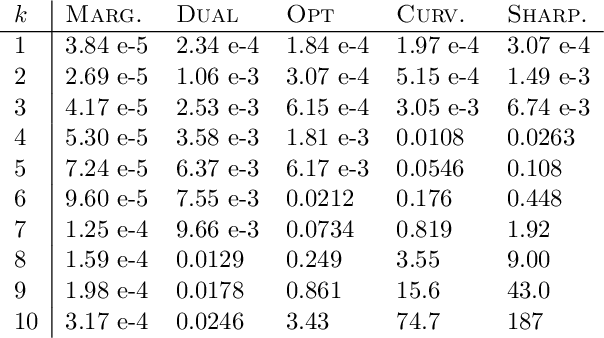
For many optimization problems in machine learning, finding an optimal solution is computationally intractable and we seek algorithms that perform well in practice. Since computational intractability often results from pathological instances, we look for methods to benchmark the performance of algorithms against optimal solutions on real-world instances. The main challenge is that an optimal solution cannot be efficiently computed for intractable problems, and we therefore often do not know how far a solution is from being optimal. A major question is therefore how to measure the performance of an algorithm in comparison to an optimal solution on instances we encounter in practice. In this paper, we address this question in the context of submodular optimization problems. For the canonical problem of submodular maximization under a cardinality constraint, it is intractable to compute a solution that is better than a $1-1/e \approx 0.63$ fraction of the optimum. Algorithms like the celebrated greedy algorithm are guaranteed to achieve this $1-1/e$ bound on any instance and are used in practice. Our main contribution is not a new algorithm for submodular maximization but an analytical method that measures how close an algorithm for submodular maximization is to optimal on a given problem instance. We use this method to show that on a wide variety of real-world datasets and objectives, the approximation of the solution found by greedy goes well beyond $1-1/e$ and is often at least 0.95. We develop this method using a novel technique that lower bounds the objective of a dual minimization problem to obtain an upper bound on the value of an optimal solution to the primal maximization problem.

Adversarial Attacks on Binary Image Recognition Systems

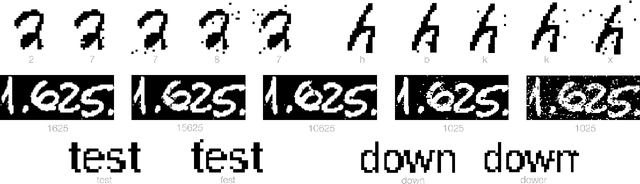
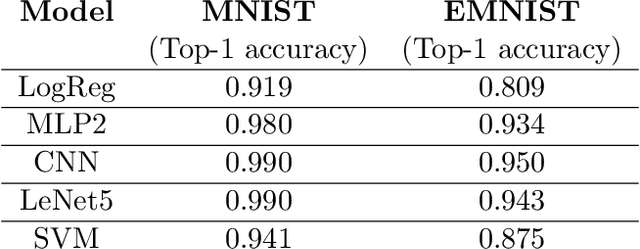
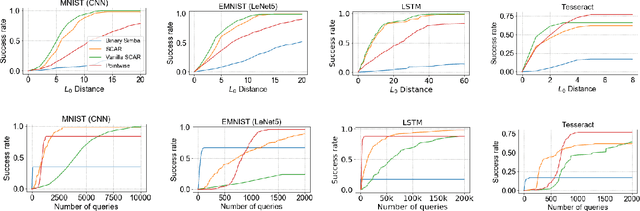
We initiate the study of adversarial attacks on models for binary (i.e. black and white) image classification. Although there has been a great deal of work on attacking models for colored and grayscale images, little is known about attacks on models for binary images. Models trained to classify binary images are used in text recognition applications such as check processing, license plate recognition, invoice processing, and many others. In contrast to colored and grayscale images, the search space of attacks on binary images is extremely restricted and noise cannot be hidden with minor perturbations in each pixel. Thus, the optimization landscape of attacks on binary images introduces new fundamental challenges. In this paper we introduce a new attack algorithm called SCAR, designed to fool classifiers of binary images. We show that SCAR significantly outperforms existing $L_0$ attacks applied to the binary setting and use it to demonstrate the vulnerability of real-world text recognition systems. SCAR's strong performance in practice contrasts with the existence of classifiers that are provably robust to large perturbations. In many cases, altering a single pixel is sufficient to trick Tesseract, a popular open-source text recognition system, to misclassify a word as a different word in the English dictionary. We also license software from providers of check processing systems to most of the major US banks and demonstrate the vulnerability of check recognitions for mobile deposits. These systems are substantially harder to fool since they classify both the handwritten amounts in digits and letters, independently. Nevertheless, we generalize SCAR to design attacks that fool state-of-the-art check processing systems using unnoticeable perturbations that lead to misclassification of deposit amounts. Consequently, this is a powerful method to perform financial fraud.

The FAST Algorithm for Submodular Maximization

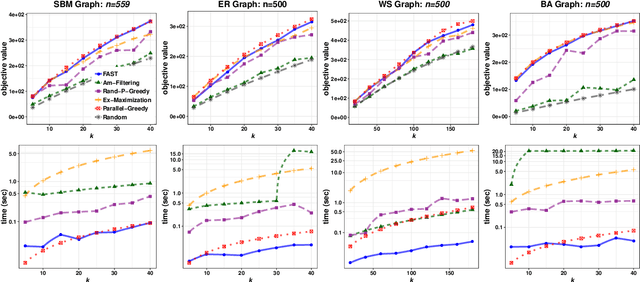
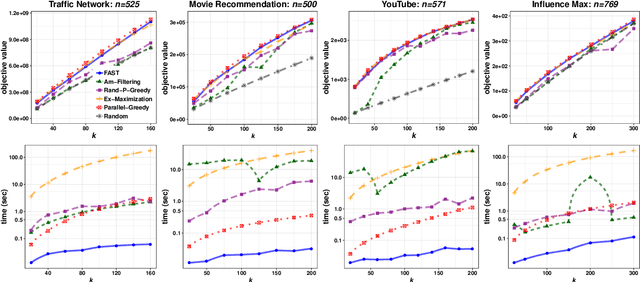
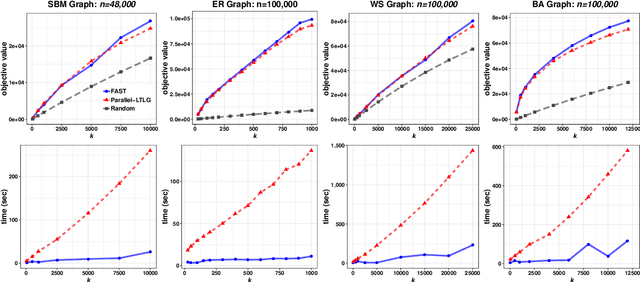
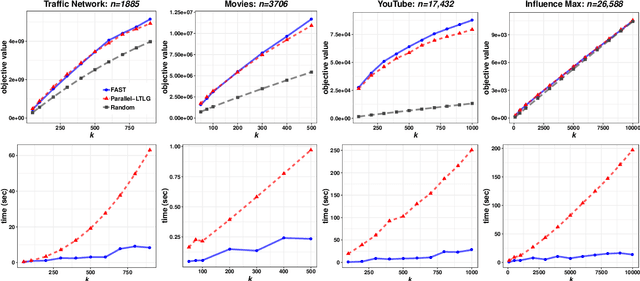
In this paper we describe a new algorithm called Fast Adaptive Sequencing Technique (FAST) for maximizing a monotone submodular function under a cardinality constraint $k$ whose approximation ratio is arbitrarily close to $1-1/e$, is $O(\log(n) \log^2(\log k))$ adaptive, and uses a total of $O(n \log\log(k))$ queries. Recent algorithms have comparable guarantees in terms of asymptotic worst case analysis, but their actual number of rounds and query complexity depend on very large constants and polynomials in terms of precision and confidence, making them impractical for large data sets. Our main contribution is a design that is extremely efficient both in terms of its non-asymptotic worst case query complexity and number of rounds, and in terms of its practical runtime. We show that this algorithm outperforms any algorithm for submodular maximization we are aware of, including hyper-optimized parallel versions of state-of-the-art serial algorithms, by running experiments on large data sets. These experiments show FAST is orders of magnitude faster than the state-of-the-art.

Parallelization does not Accelerate Convex Optimization: Adaptivity Lower Bounds for Non-smooth Convex Minimization

In this paper we study the limitations of parallelization in convex optimization. A convenient approach to study parallelization is through the prism of \emph{adaptivity} which is an information theoretic measure of the parallel runtime of an algorithm. Informally, adaptivity is the number of sequential rounds an algorithm needs to make when it can execute polynomially-many queries in parallel at every round. For combinatorial optimization with black-box oracle access, the study of adaptivity has recently led to exponential accelerations in parallel runtime and the natural question is whether dramatic accelerations are achievable for convex optimization. Our main result is a spoiler. We show that, in general, parallelization does not accelerate convex optimization. In particular, for the problem of minimizing a non-smooth Lipschitz and strongly convex function with black-box oracle access we give information theoretic lower bounds that indicate that the number of adaptive rounds of any randomized algorithm exactly match the upper bounds of single-query-per-round (i.e. non-parallel) algorithms.

Statistical Cost Sharing

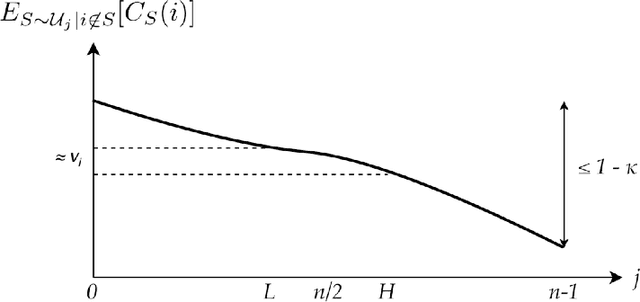
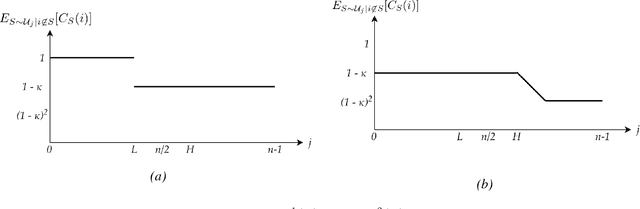
We study the cost sharing problem for cooperative games in situations where the cost function $C$ is not available via oracle queries, but must instead be derived from data, represented as tuples $(S, C(S))$, for different subsets $S$ of players. We formalize this approach, which we call statistical cost sharing, and consider the computation of the core and the Shapley value, when the tuples are drawn from some distribution $\mathcal{D}$. Previous work by Balcan et al. in this setting showed how to compute cost shares that satisfy the core property with high probability for limited classes of functions. We expand on their work and give an algorithm that computes such cost shares for any function with a non-empty core. We complement these results by proving an inapproximability lower bound for a weaker relaxation. We then turn our attention to the Shapley value. We first show that when cost functions come from the family of submodular functions with bounded curvature, $\kappa$, the Shapley value can be approximated from samples up to a $\sqrt{1 - \kappa}$ factor, and that the bound is tight. We then define statistical analogues of the Shapley axioms, and derive a notion of statistical Shapley value. We show that these can always be approximated arbitrarily well for general functions over any distribution $\mathcal{D}$.

The Limitations of Optimization from Samples

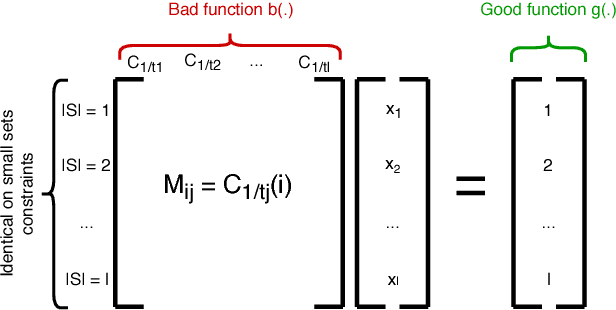
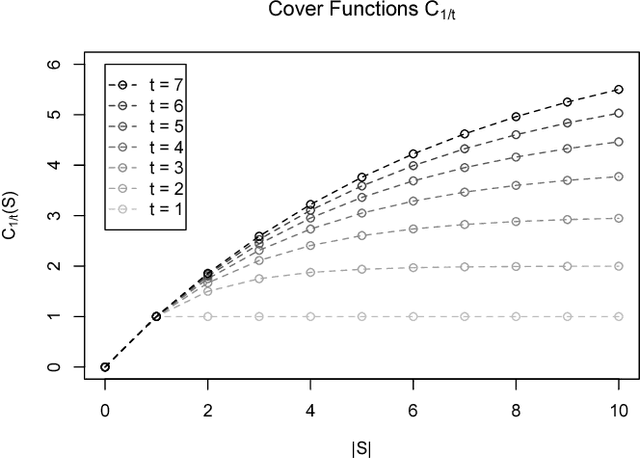
In this paper we consider the following question: can we optimize objective functions from the training data we use to learn them? We formalize this question through a novel framework we call optimization from samples (OPS). In OPS, we are given sampled values of a function drawn from some distribution and the objective is to optimize the function under some constraint. While there are interesting classes of functions that can be optimized from samples, our main result is an impossibility. We show that there are classes of functions which are statistically learnable and optimizable, but for which no reasonable approximation for optimization from samples is achievable. In particular, our main result shows that there is no constant factor approximation for maximizing coverage functions under a cardinality constraint using polynomially-many samples drawn from any distribution. We also show tight approximation guarantees for maximization under a cardinality constraint of several interesting classes of functions including unit-demand, additive, and general monotone submodular functions, as well as a constant factor approximation for monotone submodular functions with bounded curvature.