Learning Low Degree Hypergraphs

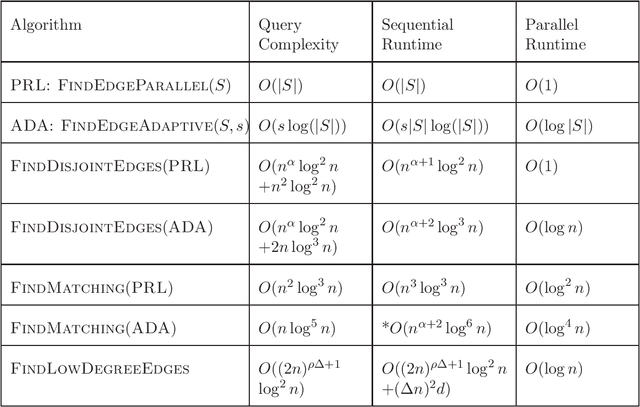
We study the problem of learning a hypergraph via edge detecting queries. In this problem, a learner queries subsets of vertices of a hidden hypergraph and observes whether these subsets contain an edge or not. In general, learning a hypergraph with $m$ edges of maximum size $d$ requires $\Omega((2m/d)^{d/2})$ queries. In this paper, we aim to identify families of hypergraphs that can be learned without suffering from a query complexity that grows exponentially in the size of the edges. We show that hypermatchings and low-degree near-uniform hypergraphs with $n$ vertices are learnable with poly$(n)$ queries. For learning hypermatchings (hypergraphs of maximum degree $ 1$), we give an $O(\log^3 n)$-round algorithm with $O(n \log^5 n)$ queries. We complement this upper bound by showing that there are no algorithms with poly$(n)$ queries that learn hypermatchings in $o(\log \log n)$ adaptive rounds. For hypergraphs with maximum degree $\Delta$ and edge size ratio $\rho$, we give a non-adaptive algorithm with $O((2n)^{\rho \Delta+1}\log^2 n)$ queries. To the best of our knowledge, these are the first algorithms with poly$(n, m)$ query complexity for learning non-trivial families of hypergraphs that have a super-constant number of edges of super-constant size.

Fast Thompson Sampling Algorithm with Cumulative Oversampling: Application to Budgeted Influence Maximization

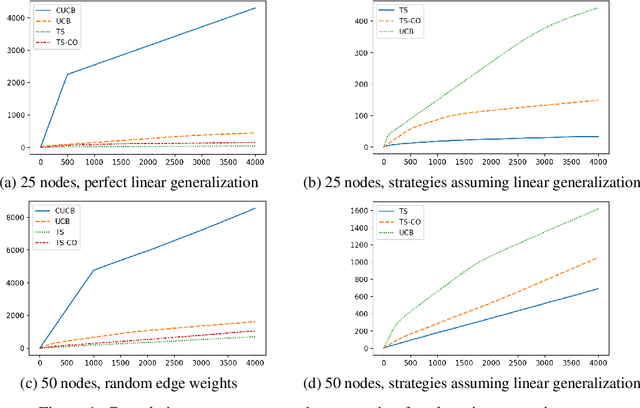
We propose a cumulative oversampling (CO) technique for Thompson Sampling (TS) that can be used to construct optimistic parameter estimates using significantly fewer samples from the posterior distributions compared to existing oversampling frameworks. We apply CO to a new budgeted variant of the Influence Maximization (IM) semi-bandits with linear generalization of edge weights. Combining CO with the oracle we designed for the offline problem, our online learning algorithm tackles the budget allocation, parameter learning, and reward maximization challenges simultaneously. We prove that our online learning algorithm achieves a scaled regret comparable to that of the UCB-based algorithms for IM semi-bandits. It is the first regret bound for TS-based algorithms for IM semi-bandits that does not depend linearly on the reciprocal of the minimum observation probability of an edge. In numerical experiments, our algorithm outperforms all UCB-based alternatives by a large margin.

Online Learning and Optimization Under a New Linear-Threshold Model with Negative Influence

We propose a new class of Linear Threshold Model-based information-diffusion model that incorporates the formation and spread of negative attitude. We call such models negativity-aware.. We show that in these models, the influence function is a monotone submodular function. Thus we can use the greedy algorithm to construct seed sets with constant approximation guarantees, when the objective is to select a seed set of fixed size $K$ to maximize total influence. Our models are flexible enough to account for both the features of local users and the features of the information being propagated in the diffusion. We analyze an online-learning setting for a multi-round influence-maximization problem, where an agent is actively learning the diffusion parameters over time while trying to maximize total cumulative influence. We assume that in each diffusion step, the agent can only observe whether a node becomes positively or negatively influenced, or remains inactive. In particular, he does not observe the particular edge that brought about the activation of a node, if any. This model of feedback is called node-level feedback, as opposed to the more common edge-level feedback model in which he is able to observe, for each node, the edge through which that node is influenced. Under mild assumptions, we develop online learning algorithms that achieve cumulative expected regrets of order $O(1/\sqrt{T})$, where $T$ is the total number of rounds. These are the first regret guarantees for node-level feedback models of influence maximization of any kind. Furthermore, with mild assumptions, this result also improves the average regret of $\mathcal{O}(\sqrt{\ln T / T})$ for the edge-level feedback model in \cite{wen2017online}, thus providing a new performance benchmark.

Beyond Adaptive Submodularity: Adaptive Influence Maximization with Intermediary Constraints

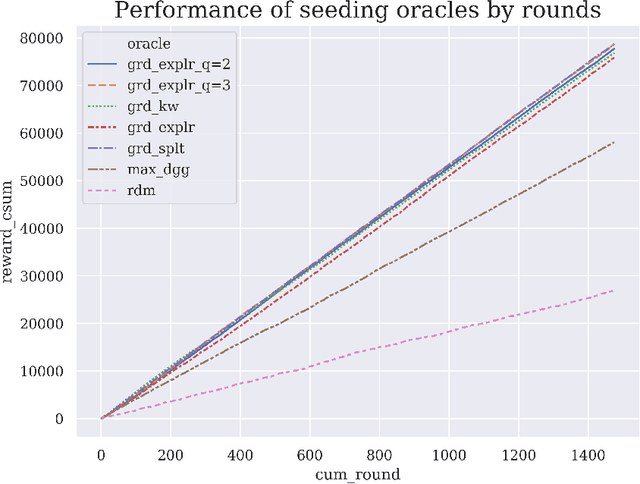
We consider a brand with a given budget that wants to promote a product over multiple rounds of influencer marketing. In each round, it commissions an influencer to promote the product over a social network, and then observes the subsequent diffusion of the product before adaptively choosing the next influencer to commission. This process terminates when the budget is exhausted. We assume that the diffusion process follows the popular Independent Cascade model. We also consider an online learning setting, where the brand initially does not know the diffusion parameters associated with the model, and has to gradually learn the parameters over time. Unlike in existing models, the rounds in our model are correlated through an intermediary constraint: each user can be commissioned for an unlimited number of times. However, each user will spread influence without commission at most once. Due to this added constraint, the order in which the influencers are chosen can change the influence spread, making obsolete existing analysis techniques that based on the notion of adaptive submodularity. We devise a sample path analysis to prove that a greedy policy that knows the diffusion parameters achieves at least $1-1/e - \epsilon$ times the expected reward of the optimal policy. In the online-learning setting, we are the first to consider a truly adaptive decision making framework, rather than assuming independent epochs, and adaptivity only within epochs. Under mild assumptions, we derive a regret bound for our algorithm. In our numerical experiments, we simulate information diffusions on four Twitter sub-networks, and compare our UCB-based learning algorithms with several baseline adaptive seeding strategies. Our learning algorithm consistently outperforms the baselines and achieves rewards close to the greedy policy that knows the true diffusion parameters.