Beyond Adaptive Submodularity: Adaptive Influence Maximization with Intermediary Constraints
Paper and Code
Nov 08, 2019
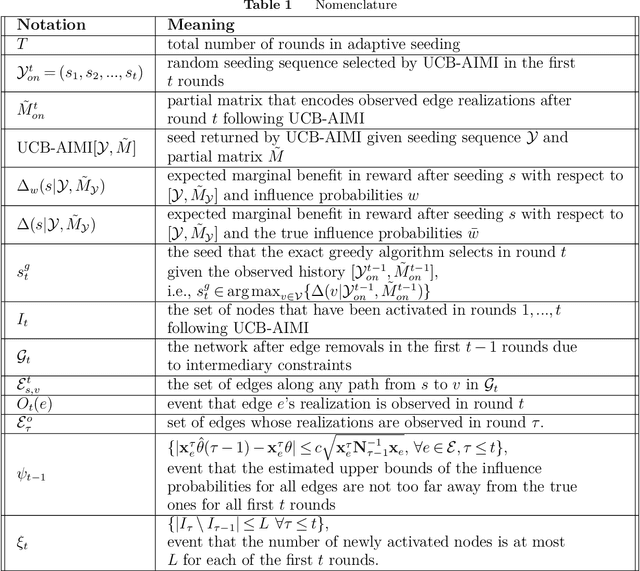

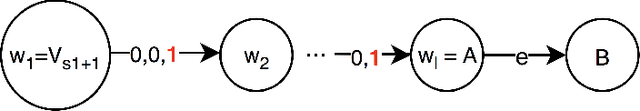
We consider a brand with a given budget that wants to promote a product over multiple rounds of influencer marketing. In each round, it commissions an influencer to promote the product over a social network, and then observes the subsequent diffusion of the product before adaptively choosing the next influencer to commission. This process terminates when the budget is exhausted. We assume that the diffusion process follows the popular Independent Cascade model. We also consider an online learning setting, where the brand initially does not know the diffusion parameters associated with the model, and has to gradually learn the parameters over time. Unlike in existing models, the rounds in our model are correlated through an intermediary constraint: each user can be commissioned for an unlimited number of times. However, each user will spread influence without commission at most once. Due to this added constraint, the order in which the influencers are chosen can change the influence spread, making obsolete existing analysis techniques that based on the notion of adaptive submodularity. We devise a sample path analysis to prove that a greedy policy that knows the diffusion parameters achieves at least $1-1/e - \epsilon$ times the expected reward of the optimal policy. In the online-learning setting, we are the first to consider a truly adaptive decision making framework, rather than assuming independent epochs, and adaptivity only within epochs. Under mild assumptions, we derive a regret bound for our algorithm. In our numerical experiments, we simulate information diffusions on four Twitter sub-networks, and compare our UCB-based learning algorithms with several baseline adaptive seeding strategies. Our learning algorithm consistently outperforms the baselines and achieves rewards close to the greedy policy that knows the true diffusion parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge