Federated Multi-Level Optimization over Decentralized Networks

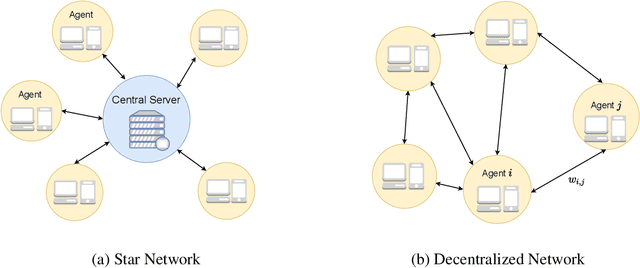
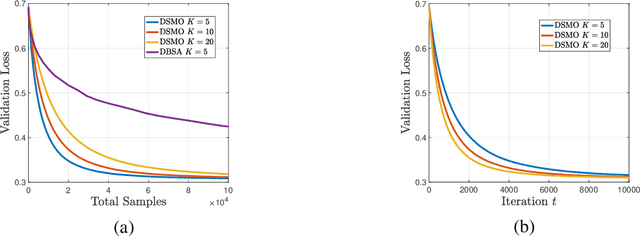
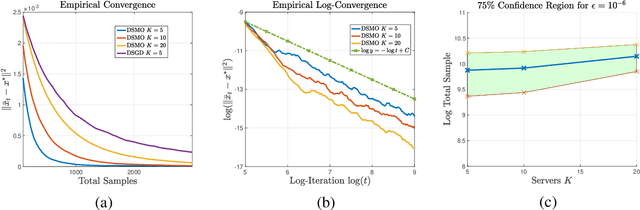
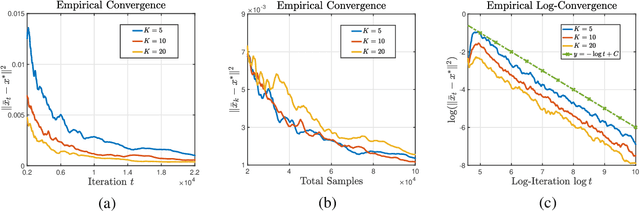
Multi-level optimization has gained increasing attention in recent years, as it provides a powerful framework for solving complex optimization problems that arise in many fields, such as meta-learning, multi-player games, reinforcement learning, and nested composition optimization. In this paper, we study the problem of distributed multi-level optimization over a network, where agents can only communicate with their immediate neighbors. This setting is motivated by the need for distributed optimization in large-scale systems, where centralized optimization may not be practical or feasible. To address this problem, we propose a novel gossip-based distributed multi-level optimization algorithm that enables networked agents to solve optimization problems at different levels in a single timescale and share information through network propagation. Our algorithm achieves optimal sample complexity, scaling linearly with the network size, and demonstrates state-of-the-art performance on various applications, including hyper-parameter tuning, decentralized reinforcement learning, and risk-averse optimization.

Streaming Sparse Linear Regression

Sparse regression has been a popular approach to perform variable selection and enhance the prediction accuracy and interpretability of the resulting statistical model. Existing approaches focus on offline regularized regression, while the online scenario has rarely been studied. In this paper, we propose a novel online sparse linear regression framework for analyzing streaming data when data points arrive sequentially. Our proposed method is memory efficient and requires less stringent restricted strong convexity assumptions. Theoretically, we show that with a properly chosen regularization parameter, the $\ell_2$-norm statistical error of our estimator diminishes to zero in the optimal order of $\tilde{O}({\sqrt{s/t}})$, where $s$ is the sparsity level, $t$ is the streaming sample size, and $\tilde{O}(\cdot)$ hides logarithmic terms. Numerical experiments demonstrate the practical efficiency of our algorithm.

Stochastic Compositional Optimization with Compositional Constraints

Stochastic compositional optimization (SCO) has attracted considerable attention because of its broad applicability to important real-world problems. However, existing works on SCO assume that the projection within a solution update is simple, which fails to hold for problem instances where the constraints are in the form of expectations, such as empirical conditional value-at-risk constraints. We study a novel model that incorporates single-level expected value and two-level compositional constraints into the current SCO framework. Our model can be applied widely to data-driven optimization and risk management, including risk-averse optimization and high-moment portfolio selection, and can handle multiple constraints. We further propose a class of primal-dual algorithms that generates sequences converging to the optimal solution at the rate of $\cO(\frac{1}{\sqrt{N}})$under both single-level expected value and two-level compositional constraints, where $N$ is the iteration counter, establishing the benchmarks in expected value constrained SCO.

Decentralized Gossip-Based Stochastic Bilevel Optimization over Communication Networks

Bilevel optimization have gained growing interests, with numerous applications found in meta learning, minimax games, reinforcement learning, and nested composition optimization. This paper studies the problem of distributed bilevel optimization over a network where agents can only communicate with neighbors, including examples from multi-task, multi-agent learning and federated learning. In this paper, we propose a gossip-based distributed bilevel learning algorithm that allows networked agents to solve both the inner and outer optimization problems in a single timescale and share information via network propagation. We show that our algorithm enjoys the $\mathcal{O}(\frac{1}{K \epsilon^2})$ per-agent sample complexity for general nonconvex bilevel optimization and $\mathcal{O}(\frac{1}{K \epsilon})$ for strongly convex objective, achieving a speedup that scales linearly with the network size. The sample complexities are optimal in both $\epsilon$ and $K$. We test our algorithm on the examples of hyperparameter tuning and decentralized reinforcement learning. Simulated experiments confirmed that our algorithm achieves the state-of-the-art training efficiency and test accuracy.

Optimality Conditions and Algorithms for Top-K Arm Identification

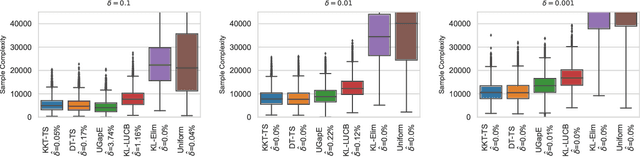
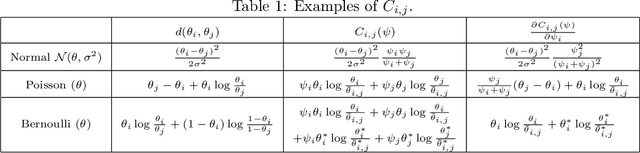
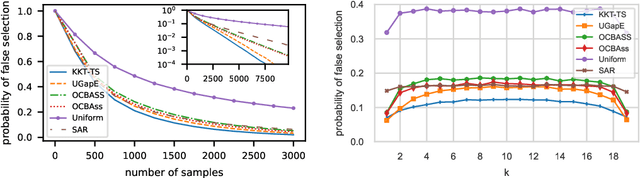
We consider the top-k arm identification problem for multi-armed bandits with rewards belonging to a one-parameter canonical exponential family. The objective is to select the set of k arms with the highest mean rewards by sequential allocation of sampling efforts. We propose a unified optimal allocation problem that identifies the complexity measures of this problem under the fixed-confidence, fixed-budget settings, and the posterior convergence rate from the Bayesian perspective. We provide the first characterization of its optimality. We provide the first provably optimal algorithm in the fixed-confidence setting for k>1. We also propose an efficient heuristic algorithm for the top-k arm identification problem. Extensive numerical experiments demonstrate superior performance compare to existing methods in all three settings.

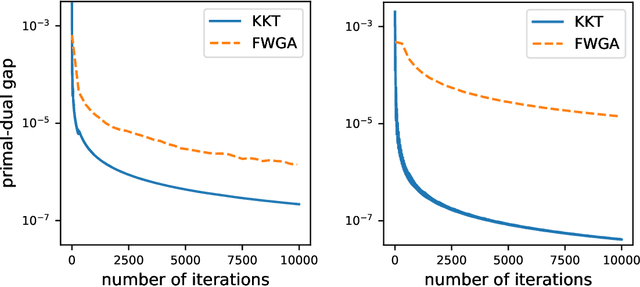
Data-Driven Minimax Optimization with Expectation Constraints

Attention to data-driven optimization approaches, including the well-known stochastic gradient descent method, has grown significantly over recent decades, but data-driven constraints have rarely been studied, because of the computational challenges of projections onto the feasible set defined by these hard constraints. In this paper, we focus on the non-smooth convex-concave stochastic minimax regime and formulate the data-driven constraints as expectation constraints. The minimax expectation constrained problem subsumes a broad class of real-world applications, including two-player zero-sum game and data-driven robust optimization. We propose a class of efficient primal-dual algorithms to tackle the minimax expectation-constrained problem, and show that our algorithms converge at the optimal rate of $\mathcal{O}(\frac{1}{\sqrt{N}})$. We demonstrate the practical efficiency of our algorithms by conducting numerical experiments on large-scale real-world applications.

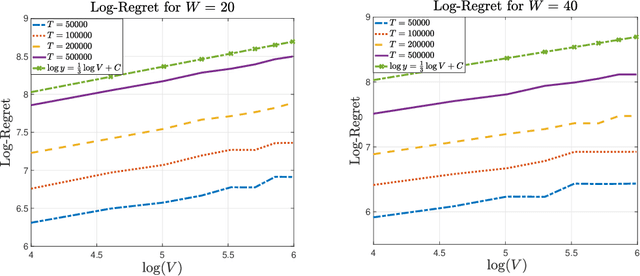
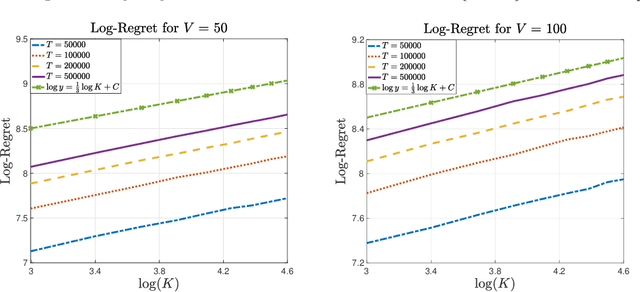
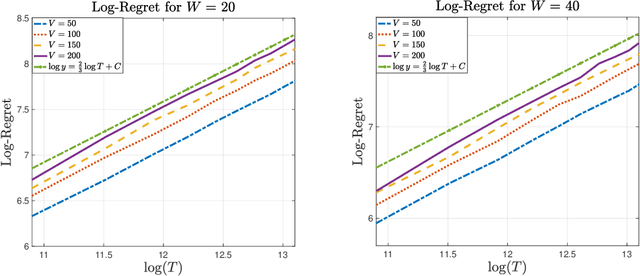
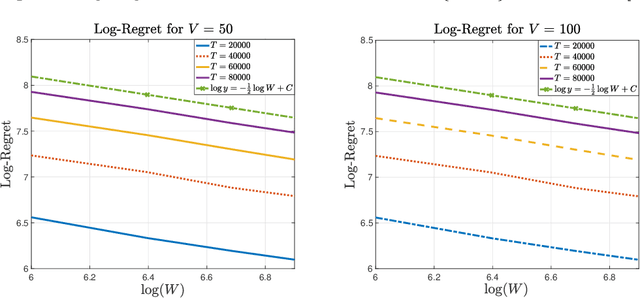
Bridging Adversarial and Nonstationary Multi-armed Bandit

In the multi-armed bandit framework, there are two formulations that are commonly employed to handle time-varying reward distributions: adversarial bandit and nonstationary bandit. Although their oracles, algorithms, and regret analysis differ significantly, we provide a unified formulation in this paper that smoothly bridges the two as special cases. The formulation uses an oracle that takes the best-fixed arm within time windows. Depending on the window size, it turns into the oracle in hindsight in the adversarial bandit and dynamic oracle in the nonstationary bandit. We provide algorithms that attain the optimal regret with the matching lower bound.

Online Learning of Independent Cascade Models with Node-level Feedback

We propose a detailed analysis of the online-learning problem for Independent Cascade (IC) models under node-level feedback. These models have widespread applications in modern social networks. Existing works for IC models have only shed light on edge-level feedback models, where the agent knows the explicit outcome of every observed edge. Little is known about node-level feedback models, where only combined outcomes for sets of edges are observed; in other words, the realization of each edge is censored. This censored information, together with the nonlinear form of the aggregated influence probability, make both parameter estimation and algorithm design challenging. We establish the first confidence-region result under this setting. We also develop an online algorithm achieving a cumulative regret of $\mathcal{O}( \sqrt{T})$, matching the theoretical regret bound for IC models with edge-level feedback.

Revenue Maximization and Learning in Products Ranking

We consider the revenue maximization problem for an online retailer who plans to display a set of products differing in their prices and qualities and rank them in order. The consumers have random attention spans and view the products sequentially before purchasing a ``satisficing'' product or leaving the platform empty-handed when the attention span gets exhausted. Our framework extends the cascade model in two directions: the consumers have random attention spans instead of fixed ones and the firm maximizes revenues instead of clicking probabilities. We show a nested structure of the optimal product ranking as a function of the attention span when the attention span is fixed and design a $1/e$-approximation algorithm accordingly for the random attention spans. When the conditional purchase probabilities are not known and may depend on consumer and product features, we devise an online learning algorithm that achieves $\tilde{\mathcal{O}}(\sqrt{T})$ regret relative to the approximation algorithm, despite of the censoring of information: the attention span of a customer who purchases an item is not observable. Numerical experiments demonstrate the outstanding performance of the approximation and online learning algorithms.

Fast Thompson Sampling Algorithm with Cumulative Oversampling: Application to Budgeted Influence Maximization

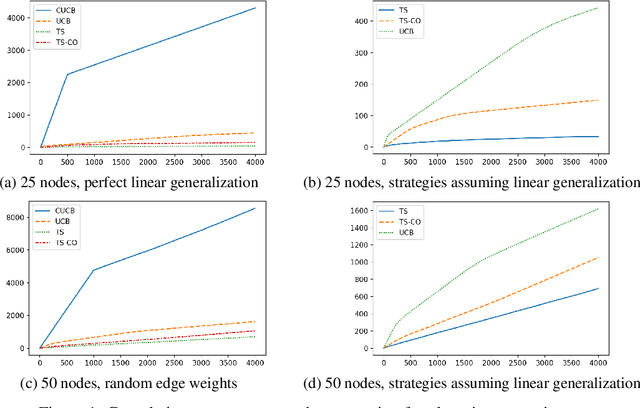
We propose a cumulative oversampling (CO) technique for Thompson Sampling (TS) that can be used to construct optimistic parameter estimates using significantly fewer samples from the posterior distributions compared to existing oversampling frameworks. We apply CO to a new budgeted variant of the Influence Maximization (IM) semi-bandits with linear generalization of edge weights. Combining CO with the oracle we designed for the offline problem, our online learning algorithm tackles the budget allocation, parameter learning, and reward maximization challenges simultaneously. We prove that our online learning algorithm achieves a scaled regret comparable to that of the UCB-based algorithms for IM semi-bandits. It is the first regret bound for TS-based algorithms for IM semi-bandits that does not depend linearly on the reciprocal of the minimum observation probability of an edge. In numerical experiments, our algorithm outperforms all UCB-based alternatives by a large margin.