Comparing Exploration-Exploitation Strategies of LLMs and Humans: Insights from Standard Multi-armed Bandit Tasks

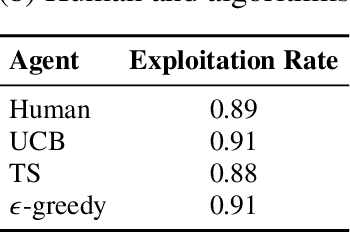
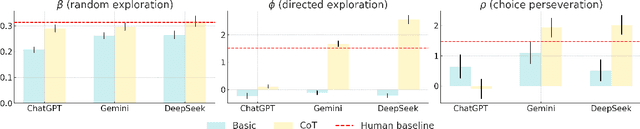
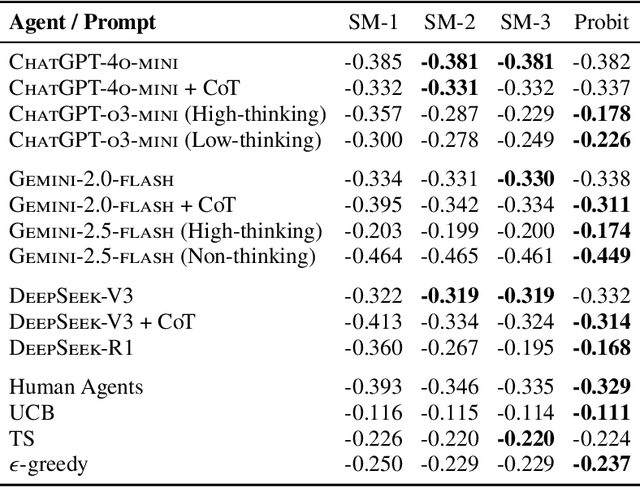
Large language models (LLMs) are increasingly used to simulate or automate human behavior in complex sequential decision-making tasks. A natural question is then whether LLMs exhibit similar decision-making behavior to humans, and can achieve comparable (or superior) performance. In this work, we focus on the exploration-exploitation (E&E) tradeoff, a fundamental aspect of dynamic decision-making under uncertainty. We employ canonical multi-armed bandit (MAB) tasks introduced in the cognitive science and psychiatry literature to conduct a comparative study of the E&E strategies of LLMs, humans, and MAB algorithms. We use interpretable choice models to capture the E&E strategies of the agents and investigate how explicit reasoning, through both prompting strategies and reasoning-enhanced models, shapes LLM decision-making. We find that reasoning shifts LLMs toward more human-like behavior, characterized by a mix of random and directed exploration. In simple stationary tasks, reasoning-enabled LLMs exhibit similar levels of random and directed exploration compared to humans. However, in more complex, non-stationary environments, LLMs struggle to match human adaptability, particularly in effective directed exploration, despite achieving similar regret in certain scenarios. Our findings highlight both the promise and limits of LLMs as simulators of human behavior and tools for automated decision-making and point to potential areas of improvements.

Reinforcement Learning for Intensity Control: An Application to Choice-Based Network Revenue Management

Intensity control is a type of continuous-time dynamic optimization problems with many important applications in Operations Research including queueing and revenue management. In this study, we adapt the reinforcement learning framework to intensity control using choice-based network revenue management as a case study, which is a classical problem in revenue management that features a large state space, a large action space and a continuous time horizon. We show that by utilizing the inherent discretization of the sample paths created by the jump points, a unique and defining feature of intensity control, one does not need to discretize the time horizon in advance, which was believed to be necessary because most reinforcement learning algorithms are designed for discrete-time problems. As a result, the computation can be facilitated and the discretization error is significantly reduced. We lay the theoretical foundation for the Monte Carlo and temporal difference learning algorithms for policy evaluation and develop policy gradient based actor critic algorithms for intensity control. Via a comprehensive numerical study, we demonstrate the benefit of our approach versus other state-of-the-art benchmarks.

Contextual Optimization under Covariate Shift: A Robust Approach by Intersecting Wasserstein Balls

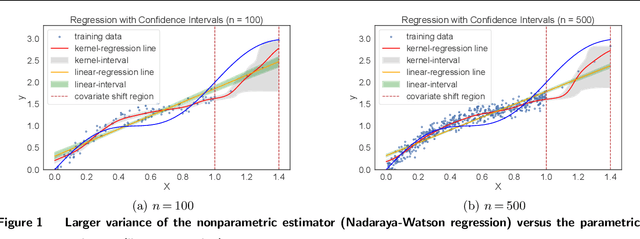
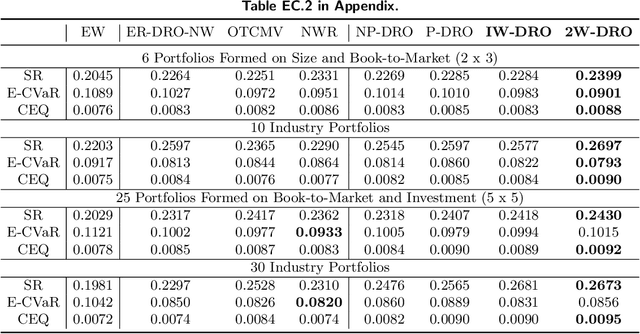
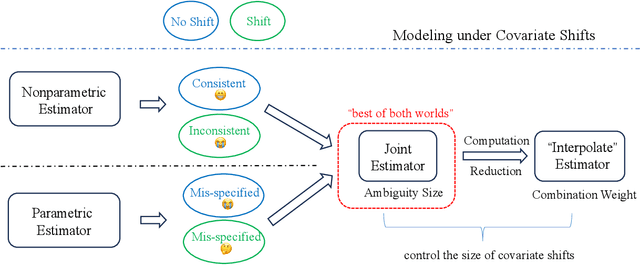
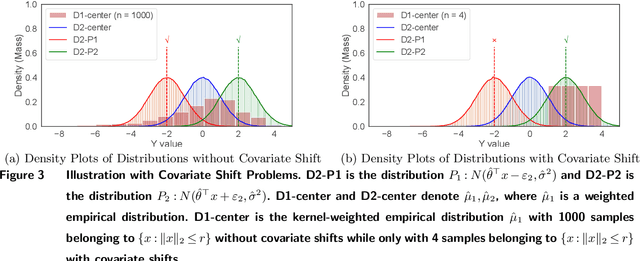
In contextual optimization, a decision-maker observes historical samples of uncertain variables and associated concurrent covariates, without knowing their joint distribution. Given an additional covariate observation, the goal is to choose a decision that minimizes some operational costs. A prevalent issue here is covariate shift, where the marginal distribution of the new covariate differs from historical samples, leading to decision performance variations with nonparametric or parametric estimators. To address this, we propose a distributionally robust approach that uses an ambiguity set by the intersection of two Wasserstein balls, each centered on typical nonparametric or parametric distribution estimators. Computationally, we establish the tractable reformulation of this distributionally robust optimization problem. Statistically, we provide guarantees for our Wasserstein ball intersection approach under covariate shift by analyzing the measure concentration of the estimators. Furthermore, to reduce computational complexity, we employ a surrogate objective that maintains similar generalization guarantees. Through synthetic and empirical case studies on income prediction and portfolio optimization, we demonstrate the strong empirical performance of our proposed models.

No Algorithmic Collusion in Two-Player Blindfolded Game with Thompson Sampling

When two players are engaged in a repeated game with unknown payoff matrices, they may be completely unaware of the existence of each other and use multi-armed bandit algorithms to choose the actions, which is referred to as the ``blindfolded game'' in this paper. We show that when the players use Thompson sampling, the game dynamics converges to the Nash equilibrium under a mild assumption on the payoff matrices. Therefore, algorithmic collusion doesn't arise in this case despite the fact that the players do not intentionally deploy competitive strategies. To prove the convergence result, we find that the framework developed in stochastic approximation doesn't apply, because of the sporadic and infrequent updates of the inferior actions and the lack of Lipschitz continuity. We develop a novel sample-path-wise approach to show the convergence.

Allocating Divisible Resources on Arms with Unknown and Random Rewards

We consider a decision maker allocating one unit of renewable and divisible resource in each period on a number of arms. The arms have unknown and random rewards whose means are proportional to the allocated resource and whose variances are proportional to an order $b$ of the allocated resource. In particular, if the decision maker allocates resource $A_i$ to arm $i$ in a period, then the reward $Y_i$ is$Y_i(A_i)=A_i \mu_i+A_i^b \xi_{i}$, where $\mu_i$ is the unknown mean and the noise $\xi_{i}$ is independent and sub-Gaussian. When the order $b$ ranges from 0 to 1, the framework smoothly bridges the standard stochastic multi-armed bandit and online learning with full feedback. We design two algorithms that attain the optimal gap-dependent and gap-independent regret bounds for $b\in [0,1]$, and demonstrate a phase transition at $b=1/2$. The theoretical results hinge on a novel concentration inequality we have developed that bounds a linear combination of sub-Gaussian random variables whose weights are fractional, adapted to the filtration, and monotonic.

Algorithmic Decision-Making Safeguarded by Human Knowledge

Commercial AI solutions provide analysts and managers with data-driven business intelligence for a wide range of decisions, such as demand forecasting and pricing. However, human analysts may have their own insights and experiences about the decision-making that is at odds with the algorithmic recommendation. In view of such a conflict, we provide a general analytical framework to study the augmentation of algorithmic decisions with human knowledge: the analyst uses the knowledge to set a guardrail by which the algorithmic decision is clipped if the algorithmic output is out of bound, and seems unreasonable. We study the conditions under which the augmentation is beneficial relative to the raw algorithmic decision. We show that when the algorithmic decision is asymptotically optimal with large data, the non-data-driven human guardrail usually provides no benefit. However, we point out three common pitfalls of the algorithmic decision: (1) lack of domain knowledge, such as the market competition, (2) model misspecification, and (3) data contamination. In these cases, even with sufficient data, the augmentation from human knowledge can still improve the performance of the algorithmic decision.

Learning Consumer Preferences from Bundle Sales Data

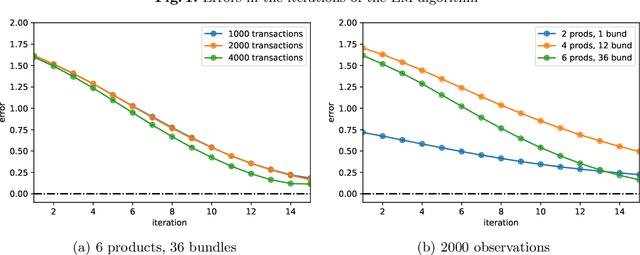
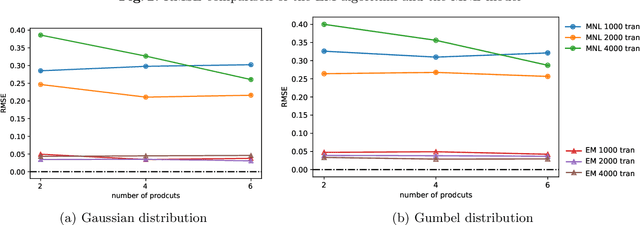
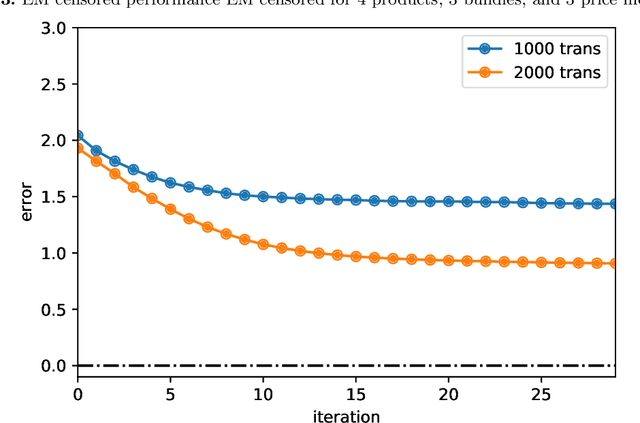
Product bundling is a common selling mechanism used in online retailing. To set profitable bundle prices, the seller needs to learn consumer preferences from the transaction data. When customers purchase bundles or multiple products, classical methods such as discrete choice models cannot be used to estimate customers' valuations. In this paper, we propose an approach to learn the distribution of consumers' valuations toward the products using bundle sales data. The approach reduces it to an estimation problem where the samples are censored by polyhedral regions. Using the EM algorithm and Monte Carlo simulation, our approach can recover the distribution of consumers' valuations. The framework allows for unobserved no-purchases and clustered market segments. We provide theoretical results on the identifiability of the probability model and the convergence of the EM algorithm. The performance of the approach is also demonstrated numerically.

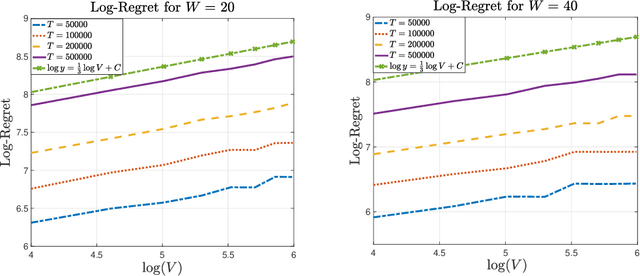
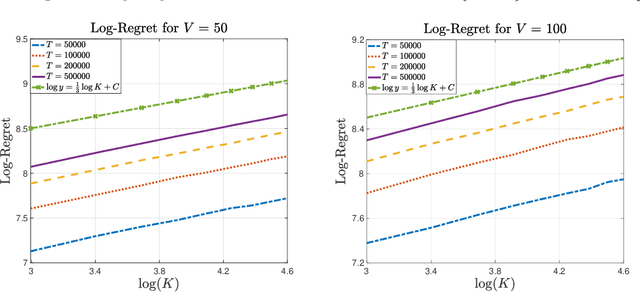
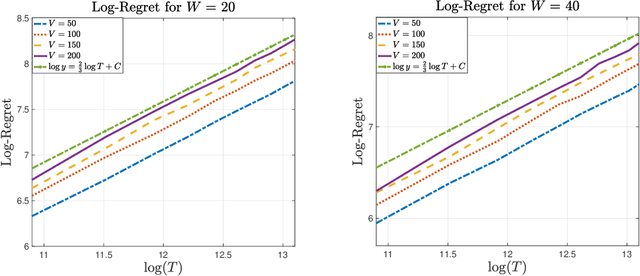
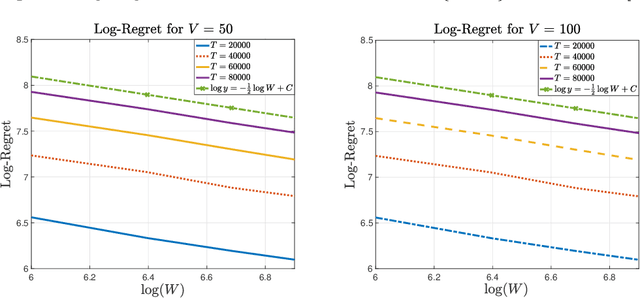
Bridging Adversarial and Nonstationary Multi-armed Bandit

In the multi-armed bandit framework, there are two formulations that are commonly employed to handle time-varying reward distributions: adversarial bandit and nonstationary bandit. Although their oracles, algorithms, and regret analysis differ significantly, we provide a unified formulation in this paper that smoothly bridges the two as special cases. The formulation uses an oracle that takes the best-fixed arm within time windows. Depending on the window size, it turns into the oracle in hindsight in the adversarial bandit and dynamic oracle in the nonstationary bandit. We provide algorithms that attain the optimal regret with the matching lower bound.

Debiasing Samples from Online Learning Using Bootstrap

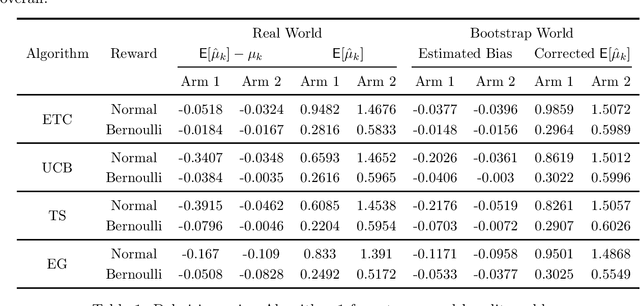
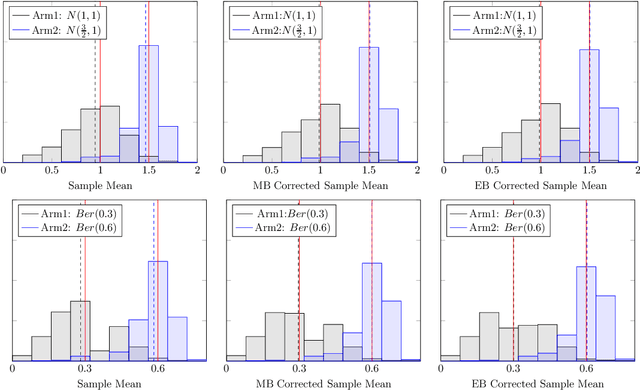
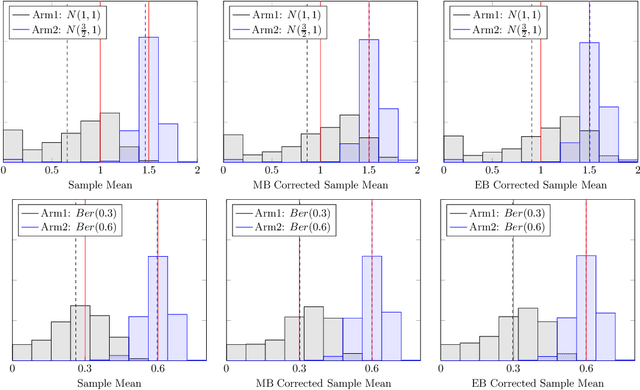
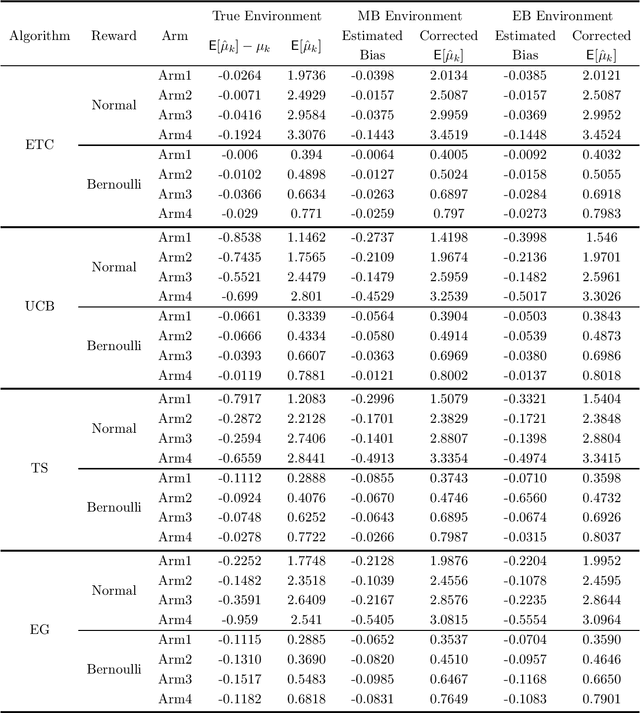
It has been recently shown in the literature that the sample averages from online learning experiments are biased when used to estimate the mean reward. To correct the bias, off-policy evaluation methods, including importance sampling and doubly robust estimators, typically calculate the propensity score, which is unavailable in this setting due to unknown reward distribution and the adaptive policy. This paper provides a procedure to debias the samples using bootstrap, which doesn't require the knowledge of the reward distribution at all. Numerical experiments demonstrate the effective bias reduction for samples generated by popular multi-armed bandit algorithms such as Explore-Then-Commit (ETC), UCB, Thompson sampling and $\epsilon$-greedy. We also analyze and provide theoretical justifications for the procedure under the ETC algorithm, including the asymptotic convergence of the bias decay rate in the real and bootstrap worlds.

Sublinear Regret for Learning POMDPs

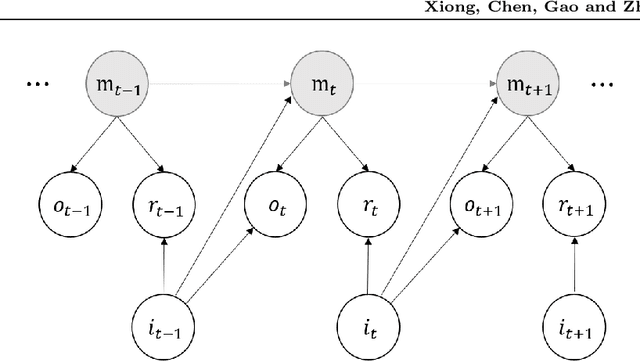
We study the model-based undiscounted reinforcement learning for partially observable Markov decision processes (POMDPs). The oracle we consider is the optimal policy of the POMDP with a known environment in terms of the average reward over an infinite horizon. We propose a learning algorithm for this problem, building on spectral method-of-moments estimations for hidden Markov models, the belief error control in POMDPs and upper-confidence-bound methods for online learning. We establish a regret bound of $O(T^{2/3}\sqrt{\log T})$ for the proposed learning algorithm where $T$ is the learning horizon. This is, to the best of our knowledge, the first algorithm achieving sublinear regret with respect to our oracle for learning general POMDPs.