Debiasing Samples from Online Learning Using Bootstrap
Paper and Code
Jul 31, 2021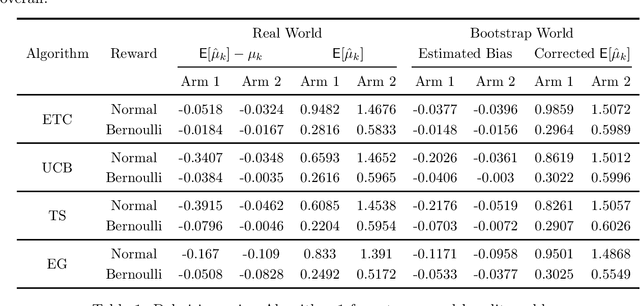
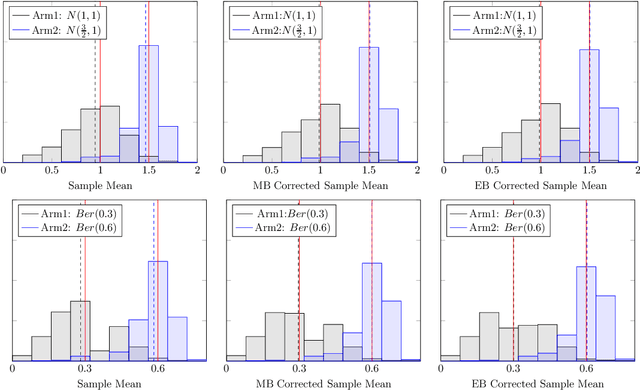
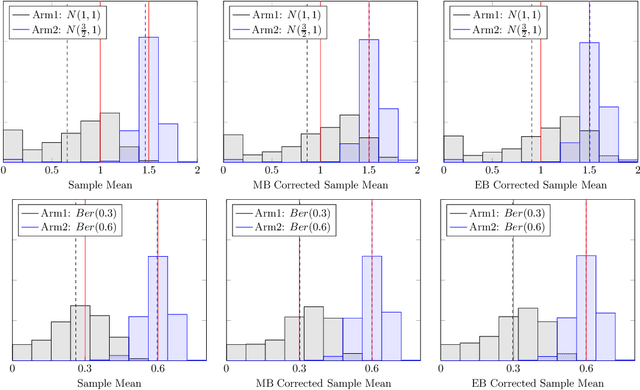
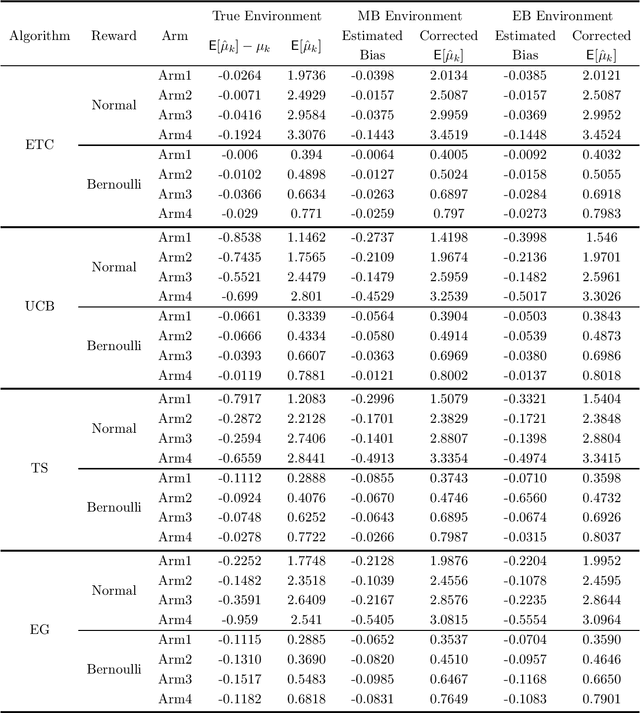
It has been recently shown in the literature that the sample averages from online learning experiments are biased when used to estimate the mean reward. To correct the bias, off-policy evaluation methods, including importance sampling and doubly robust estimators, typically calculate the propensity score, which is unavailable in this setting due to unknown reward distribution and the adaptive policy. This paper provides a procedure to debias the samples using bootstrap, which doesn't require the knowledge of the reward distribution at all. Numerical experiments demonstrate the effective bias reduction for samples generated by popular multi-armed bandit algorithms such as Explore-Then-Commit (ETC), UCB, Thompson sampling and $\epsilon$-greedy. We also analyze and provide theoretical justifications for the procedure under the ETC algorithm, including the asymptotic convergence of the bias decay rate in the real and bootstrap worlds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge