Optimality Conditions and Algorithms for Top-K Arm Identification

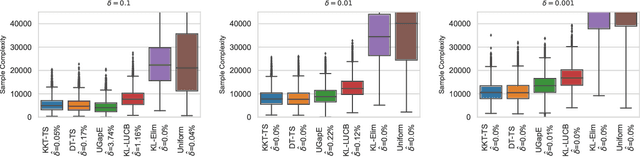
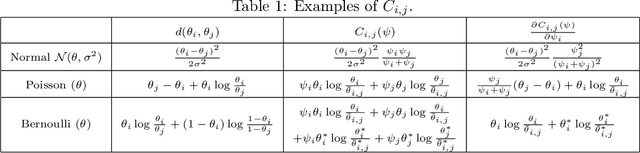
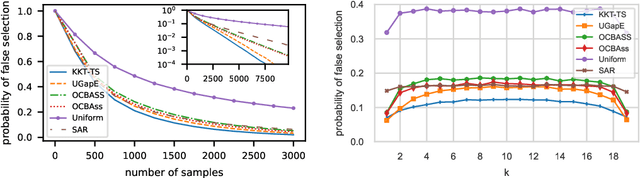
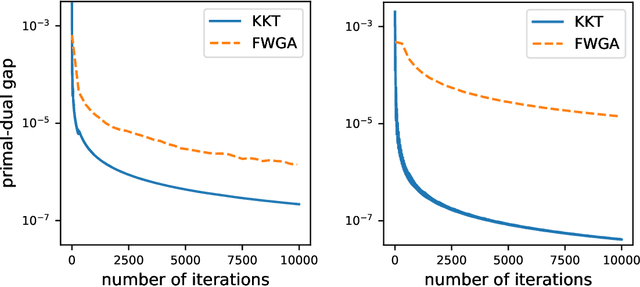
We consider the top-k arm identification problem for multi-armed bandits with rewards belonging to a one-parameter canonical exponential family. The objective is to select the set of k arms with the highest mean rewards by sequential allocation of sampling efforts. We propose a unified optimal allocation problem that identifies the complexity measures of this problem under the fixed-confidence, fixed-budget settings, and the posterior convergence rate from the Bayesian perspective. We provide the first characterization of its optimality. We provide the first provably optimal algorithm in the fixed-confidence setting for k>1. We also propose an efficient heuristic algorithm for the top-k arm identification problem. Extensive numerical experiments demonstrate superior performance compare to existing methods in all three settings.