EventAug: Multifaceted Spatio-Temporal Data Augmentation Methods for Event-based Learning

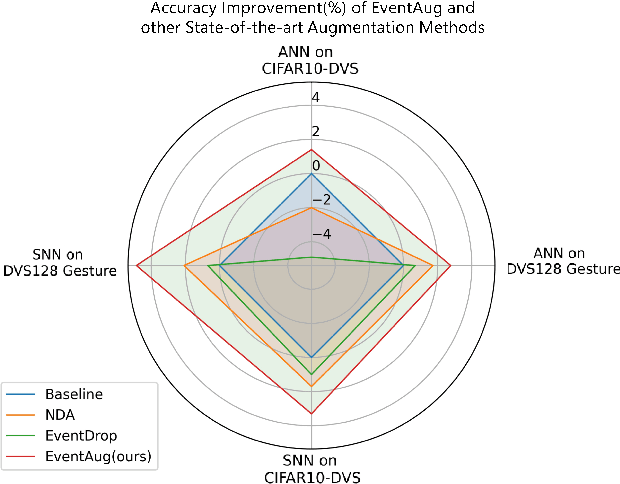
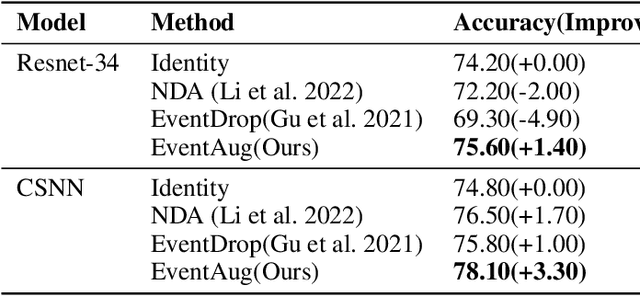
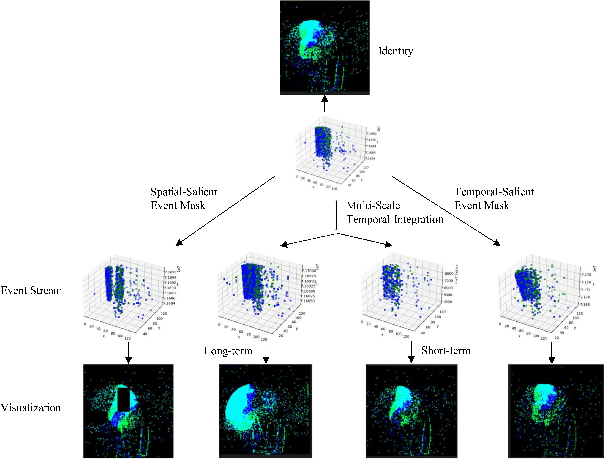
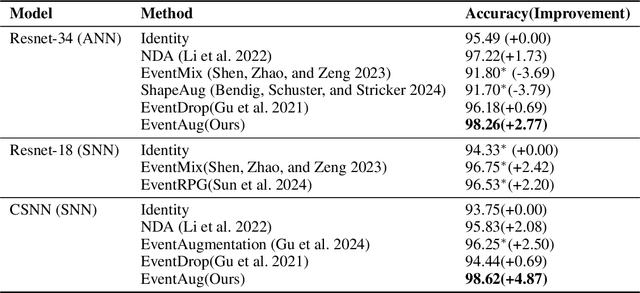
The event camera has demonstrated significant success across a wide range of areas due to its low time latency and high dynamic range. However, the community faces challenges such as data deficiency and limited diversity, often resulting in over-fitting and inadequate feature learning. Notably, the exploration of data augmentation techniques in the event community remains scarce. This work aims to address this gap by introducing a systematic augmentation scheme named EventAug to enrich spatial-temporal diversity. In particular, we first propose Multi-scale Temporal Integration (MSTI) to diversify the motion speed of objects, then introduce Spatial-salient Event Mask (SSEM) and Temporal-salient Event Mask (TSEM) to enrich object variants. Our EventAug can facilitate models learning with richer motion patterns, object variants and local spatio-temporal relations, thus improving model robustness to varied moving speeds, occlusions, and action disruptions. Experiment results show that our augmentation method consistently yields significant improvements across different tasks and backbones (e.g., a 4.87% accuracy gain on DVS128 Gesture). Our code will be publicly available for this community.

Fight Fire with Fire: Combating Adversarial Patch Attacks using Pattern-randomized Defensive Patches

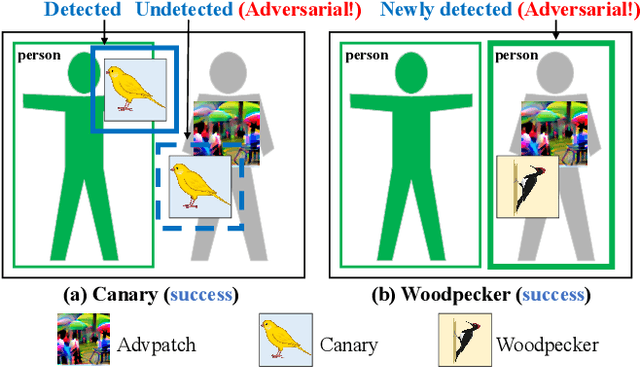
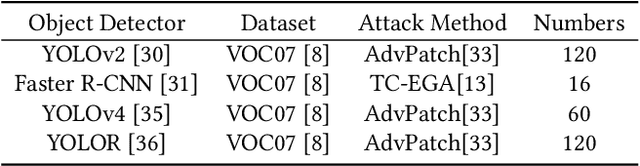
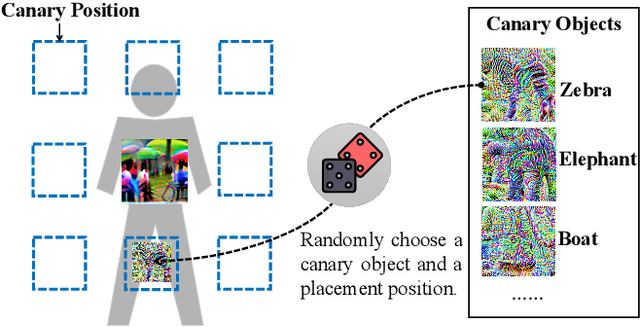
Object detection has found extensive applications in various tasks, but it is also susceptible to adversarial patch attacks. Existing defense methods often necessitate modifications to the target model or result in unacceptable time overhead. In this paper, we adopt a counterattack approach, following the principle of "fight fire with fire," and propose a novel and general methodology for defending adversarial attacks. We utilize an active defense strategy by injecting two types of defensive patches, canary and woodpecker, into the input to proactively probe or weaken potential adversarial patches without altering the target model. Moreover, inspired by randomization techniques employed in software security, we employ randomized canary and woodpecker injection patterns to defend against defense-aware attacks. The effectiveness and practicality of the proposed method are demonstrated through comprehensive experiments. The results illustrate that canary and woodpecker achieve high performance, even when confronted with unknown attack methods, while incurring limited time overhead. Furthermore, our method also exhibits sufficient robustness against defense-aware attacks, as evidenced by adaptive attack experiments.

Dual-Directed Algorithm Design for Efficient Pure Exploration

We consider pure-exploration problems in the context of stochastic sequential adaptive experiments with a finite set of alternative options. The goal of the decision-maker is to accurately answer a query question regarding the alternatives with high confidence with minimal measurement efforts. A typical query question is to identify the alternative with the best performance, leading to ranking and selection problems, or best-arm identification in the machine learning literature. We focus on the fixed-precision setting and derive a sufficient condition for optimality in terms of a notion of strong convergence to the optimal allocation of samples. Using dual variables, we characterize the necessary and sufficient conditions for an allocation to be optimal. The use of dual variables allow us to bypass the combinatorial structure of the optimality conditions that relies solely on primal variables. Remarkably, these optimality conditions enable an extension of top-two algorithm design principle, initially proposed for best-arm identification. Furthermore, our optimality conditions give rise to a straightforward yet efficient selection rule, termed information-directed selection, which adaptively picks from a candidate set based on information gain of the candidates. We outline the broad contexts where our algorithmic approach can be implemented. We establish that, paired with information-directed selection, top-two Thompson sampling is (asymptotically) optimal for Gaussian best-arm identification, solving a glaring open problem in the pure exploration literature. Our algorithm is optimal for $\epsilon$-best-arm identification and thresholding bandit problems. Our analysis also leads to a general principle to guide adaptations of Thompson sampling for pure-exploration problems. Numerical experiments highlight the exceptional efficiency of our proposed algorithms relative to existing ones.

Optimality Conditions and Algorithms for Top-K Arm Identification

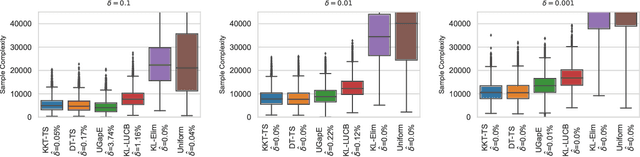
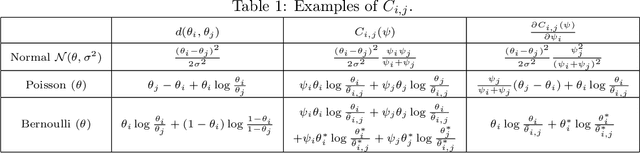
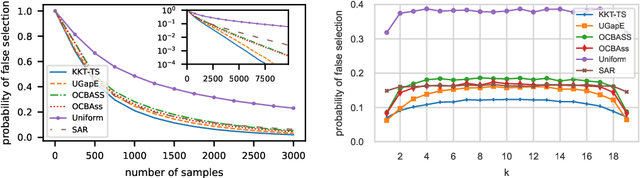
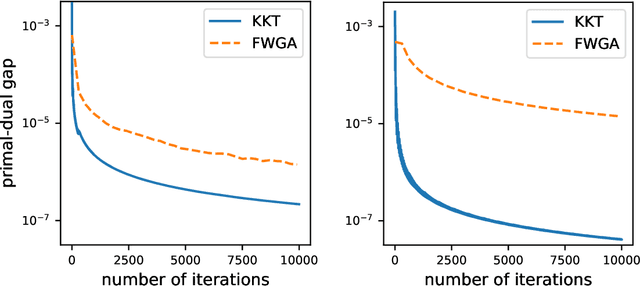
We consider the top-k arm identification problem for multi-armed bandits with rewards belonging to a one-parameter canonical exponential family. The objective is to select the set of k arms with the highest mean rewards by sequential allocation of sampling efforts. We propose a unified optimal allocation problem that identifies the complexity measures of this problem under the fixed-confidence, fixed-budget settings, and the posterior convergence rate from the Bayesian perspective. We provide the first characterization of its optimality. We provide the first provably optimal algorithm in the fixed-confidence setting for k>1. We also propose an efficient heuristic algorithm for the top-k arm identification problem. Extensive numerical experiments demonstrate superior performance compare to existing methods in all three settings.