Fast Thompson Sampling Algorithm with Cumulative Oversampling: Application to Budgeted Influence Maximization

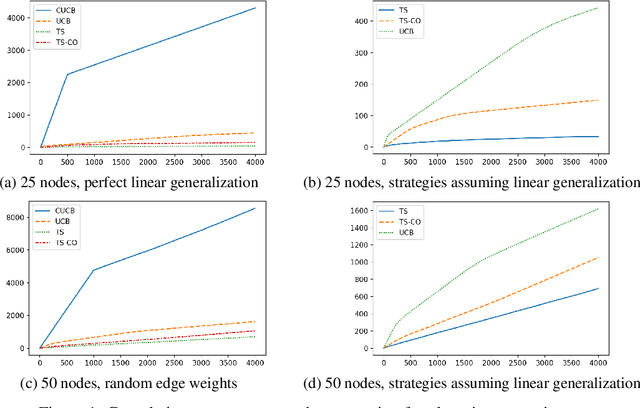
We propose a cumulative oversampling (CO) technique for Thompson Sampling (TS) that can be used to construct optimistic parameter estimates using significantly fewer samples from the posterior distributions compared to existing oversampling frameworks. We apply CO to a new budgeted variant of the Influence Maximization (IM) semi-bandits with linear generalization of edge weights. Combining CO with the oracle we designed for the offline problem, our online learning algorithm tackles the budget allocation, parameter learning, and reward maximization challenges simultaneously. We prove that our online learning algorithm achieves a scaled regret comparable to that of the UCB-based algorithms for IM semi-bandits. It is the first regret bound for TS-based algorithms for IM semi-bandits that does not depend linearly on the reciprocal of the minimum observation probability of an edge. In numerical experiments, our algorithm outperforms all UCB-based alternatives by a large margin.