Instance Specific Approximations for Submodular Maximization

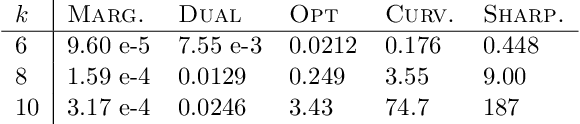
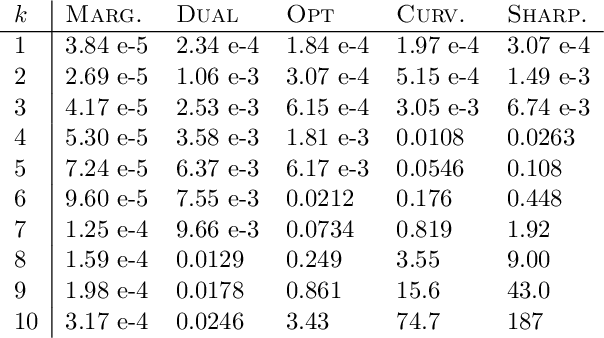
For many optimization problems in machine learning, finding an optimal solution is computationally intractable and we seek algorithms that perform well in practice. Since computational intractability often results from pathological instances, we look for methods to benchmark the performance of algorithms against optimal solutions on real-world instances. The main challenge is that an optimal solution cannot be efficiently computed for intractable problems, and we therefore often do not know how far a solution is from being optimal. A major question is therefore how to measure the performance of an algorithm in comparison to an optimal solution on instances we encounter in practice. In this paper, we address this question in the context of submodular optimization problems. For the canonical problem of submodular maximization under a cardinality constraint, it is intractable to compute a solution that is better than a $1-1/e \approx 0.63$ fraction of the optimum. Algorithms like the celebrated greedy algorithm are guaranteed to achieve this $1-1/e$ bound on any instance and are used in practice. Our main contribution is not a new algorithm for submodular maximization but an analytical method that measures how close an algorithm for submodular maximization is to optimal on a given problem instance. We use this method to show that on a wide variety of real-world datasets and objectives, the approximation of the solution found by greedy goes well beyond $1-1/e$ and is often at least 0.95. We develop this method using a novel technique that lower bounds the objective of a dual minimization problem to obtain an upper bound on the value of an optimal solution to the primal maximization problem.

Causal Mediation Analysis for Interpreting Neural NLP: The Case of Gender Bias

Common methods for interpreting neural models in natural language processing typically examine either their structure or their behavior, but not both. We propose a methodology grounded in the theory of causal mediation analysis for interpreting which parts of a model are causally implicated in its behavior. It enables us to analyze the mechanisms by which information flows from input to output through various model components, known as mediators. We apply this methodology to analyze gender bias in pre-trained Transformer language models. We study the role of individual neurons and attention heads in mediating gender bias across three datasets designed to gauge a model's sensitivity to gender bias. Our mediation analysis reveals that gender bias effects are (i) sparse, concentrated in a small part of the network; (ii) synergistic, amplified or repressed by different components; and (iii) decomposable into effects flowing directly from the input and indirectly through the mediators.

Robustness from Simple Classifiers

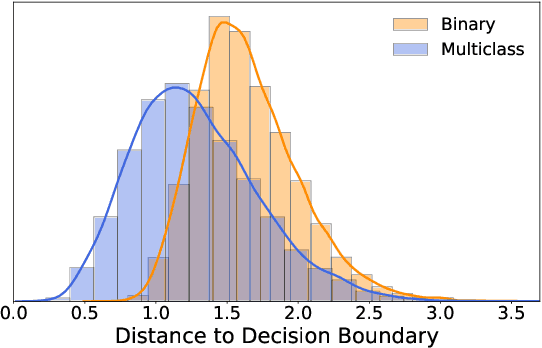
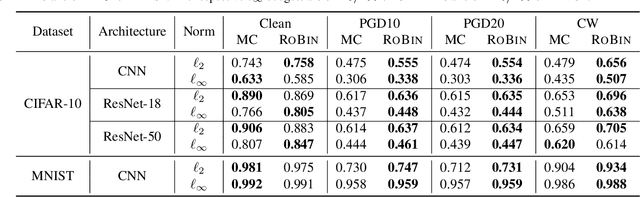
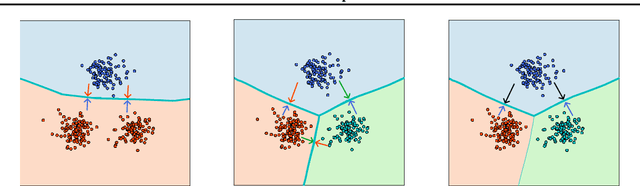
Despite the vast success of Deep Neural Networks in numerous application domains, it has been shown that such models are not robust i.e., they are vulnerable to small adversarial perturbations of the input. While extensive work has been done on why such perturbations occur or how to successfully defend against them, we still do not have a complete understanding of robustness. In this work, we investigate the connection between robustness and simplicity. We find that simpler classifiers, formed by reducing the number of output classes, are less susceptible to adversarial perturbations. Consequently, we demonstrate that decomposing a complex multiclass model into an aggregation of binary models enhances robustness. This behavior is consistent across different datasets and model architectures and can be combined with known defense techniques such as adversarial training. Moreover, we provide further evidence of a disconnect between standard and robust learning regimes. In particular, we show that elaborate label information can help standard accuracy but harm robustness.

Fast Parallel Algorithms for Feature Selection

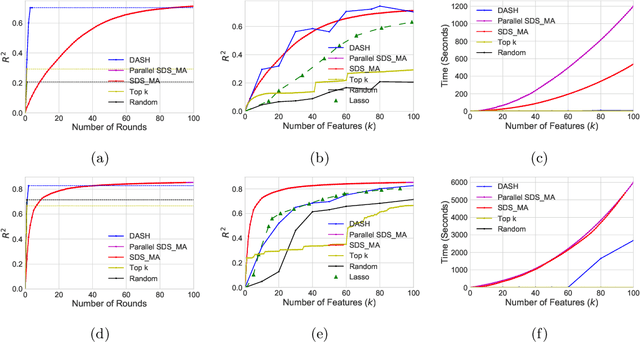
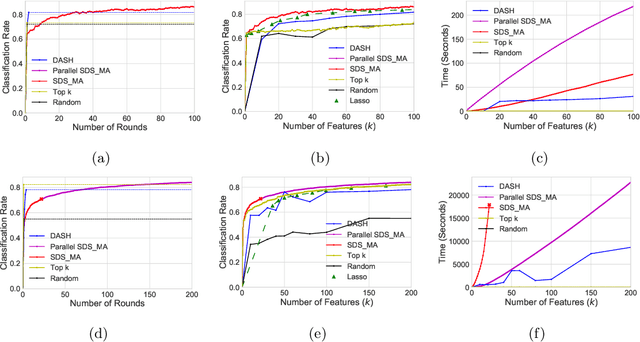
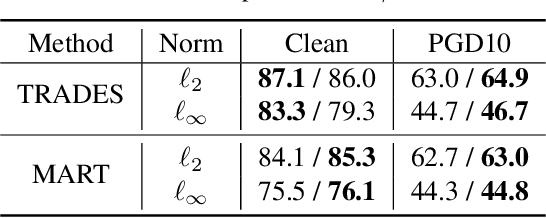
In this paper, we analyze a fast parallel algorithm to efficiently select and build a set of $k$ random variables from a large set of $n$ candidate elements. This combinatorial optimization problem can be viewed in the context of feature selection for the prediction of a response variable. Using the adaptive sampling technique, which has recently been shown to exponentially speed up submodular maximization algorithms, we propose a new parallelizable algorithm that dramatically speeds up previous selection algorithms by reducing the number of rounds from $\mathcal O(k)$ to $\mathcal O(\log n)$ for objectives that do not conform to the submodularity property. We introduce a new metric to quantify the closeness of the objective function to submodularity and analyze the performance of adaptive sampling under this regime. We also conduct experiments on synthetic and real datasets and show that the empirical performance of adaptive sampling on not-submodular objectives greatly outperforms its theoretical lower bound. Additionally, the empirical running time drastically improved in all experiments without comprising the terminal value, showing the practicality of adaptive sampling.