Fast Parallel Algorithms for Feature Selection

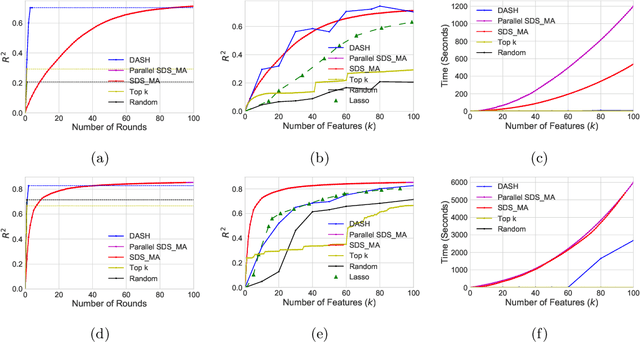
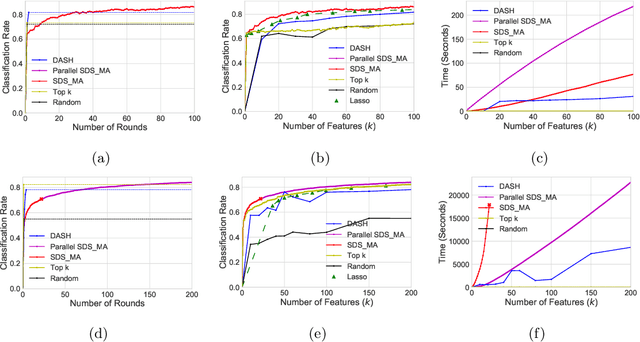
In this paper, we analyze a fast parallel algorithm to efficiently select and build a set of $k$ random variables from a large set of $n$ candidate elements. This combinatorial optimization problem can be viewed in the context of feature selection for the prediction of a response variable. Using the adaptive sampling technique, which has recently been shown to exponentially speed up submodular maximization algorithms, we propose a new parallelizable algorithm that dramatically speeds up previous selection algorithms by reducing the number of rounds from $\mathcal O(k)$ to $\mathcal O(\log n)$ for objectives that do not conform to the submodularity property. We introduce a new metric to quantify the closeness of the objective function to submodularity and analyze the performance of adaptive sampling under this regime. We also conduct experiments on synthetic and real datasets and show that the empirical performance of adaptive sampling on not-submodular objectives greatly outperforms its theoretical lower bound. Additionally, the empirical running time drastically improved in all experiments without comprising the terminal value, showing the practicality of adaptive sampling.