Robustness from Simple Classifiers

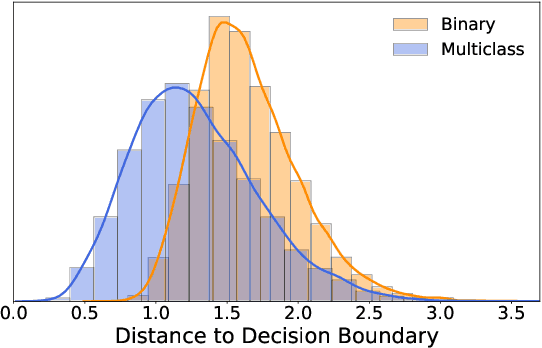
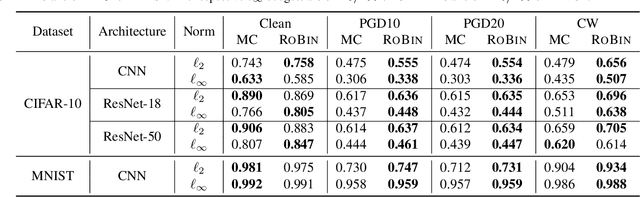
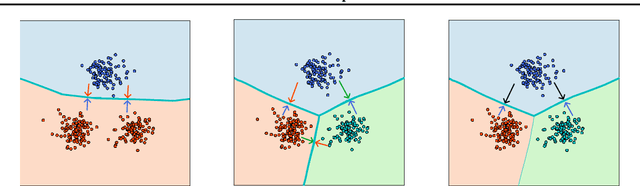
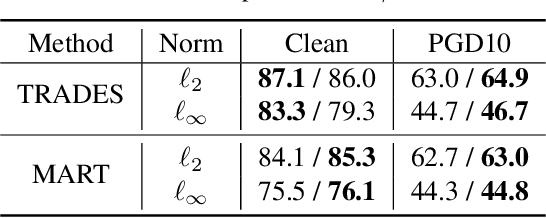
Despite the vast success of Deep Neural Networks in numerous application domains, it has been shown that such models are not robust i.e., they are vulnerable to small adversarial perturbations of the input. While extensive work has been done on why such perturbations occur or how to successfully defend against them, we still do not have a complete understanding of robustness. In this work, we investigate the connection between robustness and simplicity. We find that simpler classifiers, formed by reducing the number of output classes, are less susceptible to adversarial perturbations. Consequently, we demonstrate that decomposing a complex multiclass model into an aggregation of binary models enhances robustness. This behavior is consistent across different datasets and model architectures and can be combined with known defense techniques such as adversarial training. Moreover, we provide further evidence of a disconnect between standard and robust learning regimes. In particular, we show that elaborate label information can help standard accuracy but harm robustness.

SGD on Neural Networks Learns Functions of Increasing Complexity

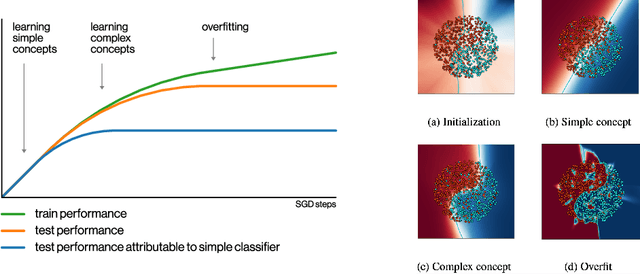
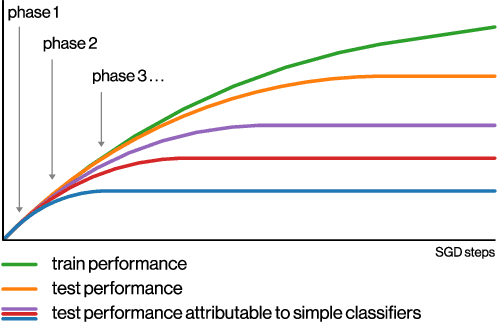
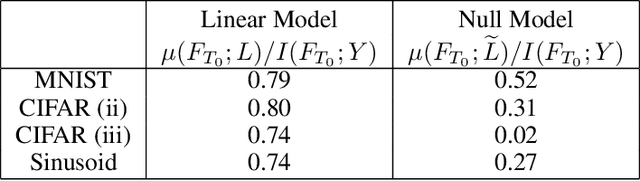
We perform an experimental study of the dynamics of Stochastic Gradient Descent (SGD) in learning deep neural networks for several real and synthetic classification tasks. We show that in the initial epochs, almost all of the performance improvement of the classifier obtained by SGD can be explained by a linear classifier. More generally, we give evidence for the hypothesis that, as iterations progress, SGD learns functions of increasing complexity. This hypothesis can be helpful in explaining why SGD-learned classifiers tend to generalize well even in the over-parameterized regime. We also show that the linear classifier learned in the initial stages is "retained" throughout the execution even if training is continued to the point of zero training error, and complement this with a theoretical result in a simplified model. Key to our work is a new measure of how well one classifier explains the performance of another, based on conditional mutual information.

Robust Influence Maximization for Hyperparametric Models

In this paper we study the problem of robust influence maximization in the independent cascade model under a hyperparametric assumption. In social networks users influence and are influenced by individuals with similar characteristics and as such they are associated with some features. A recent surging research direction in influence maximization focuses on the case where the edge probabilities on the graph are not arbitrary but are generated as a function of the features of the users and a global hyperparameter. We propose a model where the objective is to maximize the worst-case number of influenced users for any possible value of that hyperparameter. We provide theoretical results showing that proper robust solution in our model is NP-hard and an algorithm that achieves improper robust optimization. We make-use of sampling based techniques and of the renowned multiplicative weight updates algorithm. Additionally we validate our method empirically and prove that it outperforms the state-of-the-art robust influence maximization techniques.